(转)Python- sklearn之最小二乘法

最小二乘法：https://baike.baidu.com/item/%E6%9C%80%E5%B0%8F%E4%BA%8C%E4%B9%98%E6%B3%95/2522346?fr=aladdin

原文链接：https://blog.csdn.net/sinat_23338865/article/details/80608834

1.背景:

1801年，意大利天文学家朱赛普·皮亚齐发现了第一颗小行星谷神星。经过40天的跟踪观测后，由于谷神星运行至太阳背后，使得皮亚齐失去了谷神星的位置。随后全世界的科学家利用皮亚齐的观测数据开始寻找谷神星，但是根据大多数人计算的结果来寻找谷神星都没有结果。时年24岁的高斯也计算了谷神星的轨道。奥地利天文学家海因里希·奥伯斯根据高斯计算出来的轨道重新发现了谷神星。

高斯使用的最小二乘法的方法发表于1809年他的著作《天体运动论》中，而法国科学家勒让德于1806年独立发现“最小二乘法”，但因不为世人所知而默默无闻。两人曾为谁最早创立最小二乘法原理发生争执。

1829年，高斯提供了最小二乘法的优化效果强于其他方法的证明，见高斯-马尔可夫定理。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　----维基百科

2. 最小二乘法在机器学习中被用来

3. 高中关于最小二乘法估计

概括:

假设有若干个样本点,(x1,y1),(x2,y2),(x3,y3),(x4,y4),(x5,y5),求解直线y=kx+b,是的这些样本点到直线的距离最小.

我们高中的求解方式也是这样的:

展开为:

min_sum = [y1- (kx1+b)]^2+[y2- (kx2+b)]^2+[y3- (kx3+b)]^2+[y4- (kx4+b)]^2+[y5- (kx5+b)]^2

就是各个点到我们设定的直线的欧式距离

化简为:

　　　　　

以上就是我们高中对于最小二乘法的最初认知. 这个求解的过程,我们称之为最小二乘法,而求解的这条直线,我们称之为线性回归,线性回归用来近似的预测数据的真是情况.

举个例子:(此题来自:北师大版高中数学)

从某所高中随机抽取一些可爱的萌妹子,就比如6个女生好了,测出她们的体重和身高如下表,现在来了一个60kg的女生,求问它的身高会有多高?

女生数据

女生ID
身高
体重

　　　　　　

用python画图来表示这些数据好了:

 1 # encoding: utf8
 2 import matplotlib
 3 import matplotlib.pyplot as plt
 4 from matplotlib.font_manager import FontProperties
 5 from sklearn.linear_model import LinearRegression
 6 from scipy import sparse
 7
 8 print matplotlib.matplotlib_fname()  # 将会获得matplotlib包所在文件夹
 9 font = FontProperties()
10 plt.rcParams['font.sans-serif'] = ['Droid Sans Fallback']  # 指定默认字体
11 plt.rcParams['axes.unicode_minus'] = False  # 解决保存图像是负号'-'显示为方块的问题
12
13 plt.figure()
14 plt.title(u' 可爱女生的数据 ')
15 plt.xlabel(u'x 体重')
16 plt.ylabel(u'y 身高')
17 plt.axis([40, 80, 140, 200])
18 plt.grid(True)
19 x = [[48], [57], [50], [54], [64], [61], [43], [59]]
20 y = [[165], [165], [157], [170], [175], [165], [155], [170]]
21 plt.plot(x, y, 'k.')
22 model = LinearRegression()
23 model.fit(x, y)
24 # y2 = model.predict(x)
25 # plt.plot(x, y2, 'g-')
26 plt.show()

散点图:

对于这个例子,我们可以使用上面的公式,求解出回归方程,并可以得到方程拟合的该女生的身高值,但是这太麻烦了 , 毕竟高中还是太too yong too simple了~

4. 大学关于最小二乘法

基于上面的那个问题,我们大学有没有更好的一点的求解方式 ?

4.1 大学对于最小二乘法的概括:

　　　　      找到那样一条函数曲线使得观测值的残差平方之和最小. 　　通俗的讲:见高中部分概括

4.2 继续上面的这个问题思路:

　　我们已知这些数据:

　　　　  f(x,y) = [y1- (kx1+b)]^2+[y2- (kx2+b)]^2+[y3- (kx3+b)]^2+[y4- (kx4+b)]^2+[y5- (kx5+b)]^2+[y6- (kx6+b)]^2+[y7- (kx7+b)]^2+[y7- (kx7+b)]^2

如果存在最大值,那么只需要满足f(x,y)对于x,y的一阶偏导数均为0

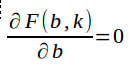
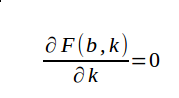
求解得:

k= 0.849  , b =85.172

所以预测值为:

y = 0.849x - 85.172  将y = 60kg  代入求解得:  x = 170.99175

我们再使用Python求解一次:

 1 # encoding: utf8
 2 import matplotlib
 3 import matplotlib.pyplot as plt
 4 from matplotlib.font_manager import FontProperties
 5 from scipy.optimize import leastsq
 6 from sklearn.linear_model import LinearRegression
 7 from scipy import sparse
 8 import numpy as np
 9
10 # 拟合函数
11 def func(a, x):
12     k, b = a
13     return k * x + b
14
15
16 # 残差
17 def dist(a, x, y):
18     return func(a, x) - y
19
20
21 font = FontProperties()
22 plt.rcParams['font.sans-serif'] = ['Droid Sans Fallback']  # 指定默认字体
23 plt.rcParams['axes.unicode_minus'] = False  # 解决保存图像是负号'-'显示为方块的问题
24
25 plt.figure()
26 plt.title(u' 可爱女生的数据 ')
27 plt.xlabel(u'x 体重')
28 plt.ylabel(u'y 身高')
29 plt.axis([40, 80, 140, 200])
30 plt.grid(True)
31 x = np.array([48.0, 57.0, 50.0,54.0, 64.0, 61.0, 43.0, 59.0])
32 y = np.array([165.0, 165.0,157.0, 170.0, 175.0, 165.0, 155.0, 170.0])
33 plt.plot(x, y, 'k.')
34
35 param = [0, 0]
36
37 var= leastsq(dist, param, args=(x, y))
38 k, b = var[0]
39 print k, b
40
41 plt.plot(x, k*x+b, 'o-')
42
43 plt.show()

从图中,可以发现结果大致相符.

关于leastsq备注：

scipy库中的函数，它可以省去中间那些具体的求解步骤，只需要输入一系列样本点，给出待求函数的基本形状（如一元一次函数，或者二元二次函数就是一种形状——f(x,y)=w0x^2+w1y^2+w2xy+w3x+w4y+w5，在形状给定后，我们只需要求解相应的系数w0~w6），即可得到相应的参数。至于中间到底是怎么求的，这一部分内容就像一个黑箱一样。