【数据结构】线段树(Segment Tree)
假设我们现在拿到了一个非常大的数组,对于这个数组里面的数字要反复不断地做两个操作。

1、(query)随机在这个数组中选一个区间,求出这个区间所有数的和。
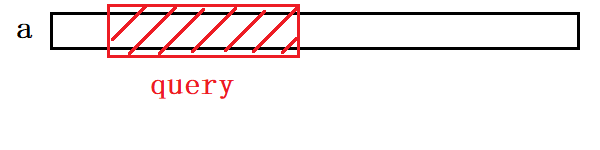
2、(update)不断地随机修改这个数组中的某一个值。

时间复杂度:
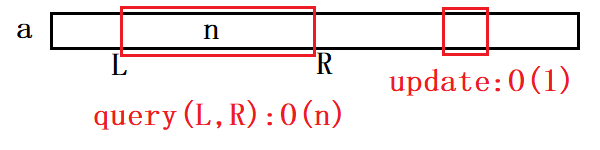
枚举:
枚举L~R的每个数并累加。
- query:O(n)
找到要修改的数直接修改。
- update:O(1)
如果query与update要做很多很多次,query的O(n)会被卡住,所以时间复杂度会非常慢。那么有没有办法把query的时间复杂度降成O(1)呢?其中一种方法如下:
- 先建立一个与a数组一样大的数组。
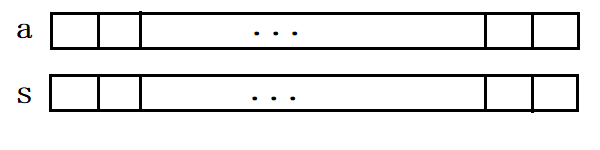
- s[1]=a[1];s[2]=a[1]+a[2];s[3]=a[1]+a[2]+a[3];...;s[n]=a[1]+a[2]+a[3]+...+a[n](在s数组中存入a的前缀和)
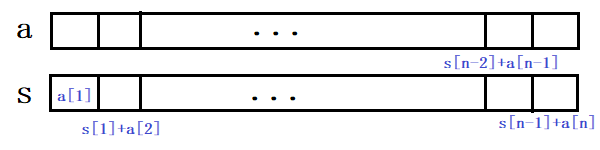
- 此时a[L]+a[L+1]+...+a[R]=s[R]-s[L-1],query的时间复杂度降为O(1)。
- 但若要修改a[k]的值,随之也需修改s[k],s[k+1],...,s[n]的值,时间复杂度升为O(n)。
前缀和:
query:O(1)
update:O(n)
- 我们发现,当我们想尽方法把其中一个操作的时间复杂度改成O(1)后,另一个操作的时间复杂度就会变为O(n)。当query与update的操作特别多时,不论用哪种方法,总体的时间复杂度都不会特别快。
- 所以,我们将要讨论一种叫线段树的数据结构,它可以把这两个操作的时间复杂度平均一下,使得query和update的时间复杂度都落在O(n log n)上,从而增加整个算法的效率。
线段树
假设我们拿到了如下长度为6的数组:

在构建线段树之前,我们先阐述线段树的性质:
1、线段树的每个节点都代表一个区间。
2、线段树具有唯一的根节点,代表的区间是整个统计范围,如[1,N]。
3、线段树的每个叶节点都代表一个长度为1的元区间[x,x]。
4、对于每个内部节点[l,r],它的左子结点是[l,mid],右子节点是[mid+1,r],其中mid=(l+r)/2(向下取整)。
依照这个数组,我们构建如下线段树(结点的性质为sum):
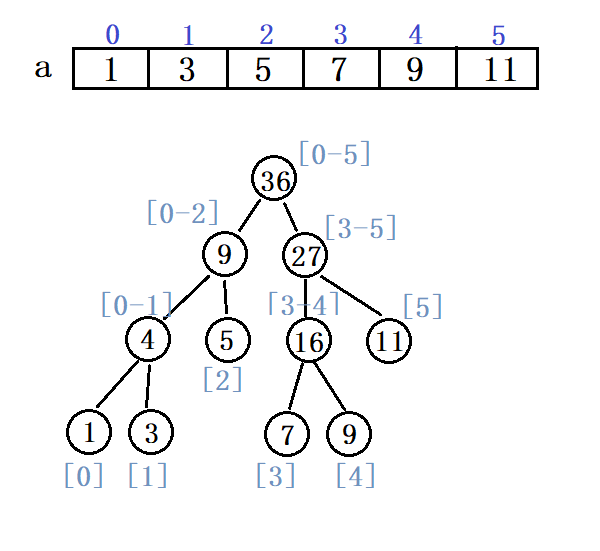
若我们要求[2-5]区间中数的和:
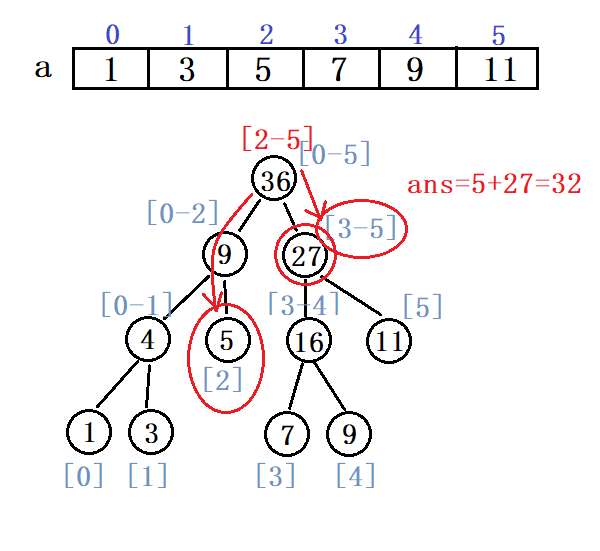
若我们要把a[4]改为6:
- 先一层一层找到目标节点修改,在依次向上修改当前节点的父节点。
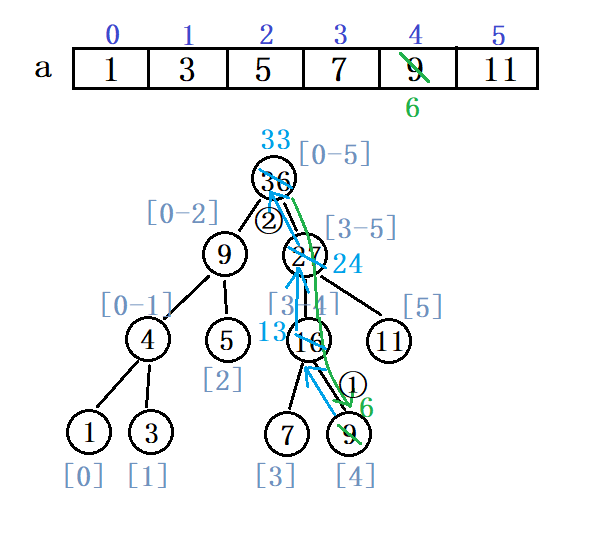
接下来的问题是:如何保存这棵线段树?
- 用数组存储。
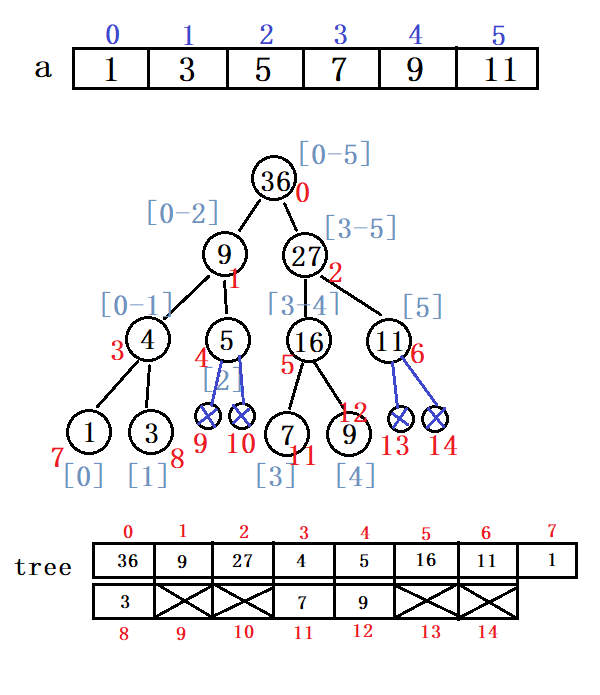
若我们要取node结点的左子结点(left)与右子节点(right),方法如下:
- left=2*node+1
- right=2*ndoe+2
举结点5为例(左子结点为节点11,右子节点为节点12):
- left5=2*5+1=11
- right5=2*5+2=12
接下来给出建树的代码:
#include<bits/stdc++.h>
using namespace std; const int N = ; int a[] = {, , , , , };
int size = ;
int tree[N] = {}; //建立范围为a[start]~a[end]
void build(int a[], int tree[], int node/*当前节点*/, int start, int end){
//递归边界(即遇到叶子节点时)
if (start == end){
//直接存储a数组中的值
tree[node] = a[start];
} else {
//将建立的区间分成两半
int mid = (start + end) / ; int left = * node + ;//左子节点的下标
int right = * node + ;//右子节点的下标 //求出左子节点的值(即从节点left开始,建立范围为a[start]~a[mid])
build(a, tree, left, start, mid);
//求出右子节点的值(即从节点right开始,建立范围为a[start]~a[mid])
build(a, tree, right, mid+, end); //当前节点的职位左子节点的值加上右子节点的值
tree[node] = tree[left] + tree[right];
}
} int main(){
//从根节点(即节点0)开始建树,建树范围为a[0]~a[size-1]
build(a, tree, , , size-); for(int i = ; i <= ; i ++)
printf("tree[%d] = %d\n", i, tree[i]); return ;
}
运行结果:
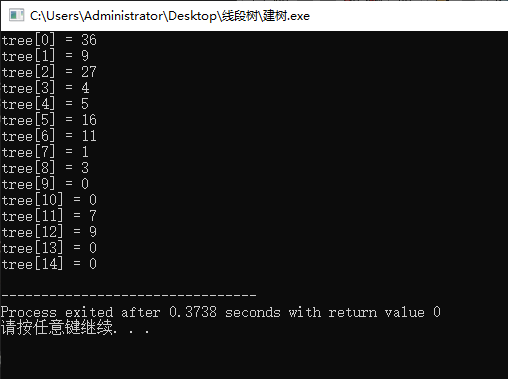
update操作:
- 确定需要改的分支,向下寻找需要修改的节点,再向上修改节点值。
- 与建树的函数相比,update函数增加了两个参数x,val,即把a[x]改为val。
例:把a[x]改为6(代码实现)
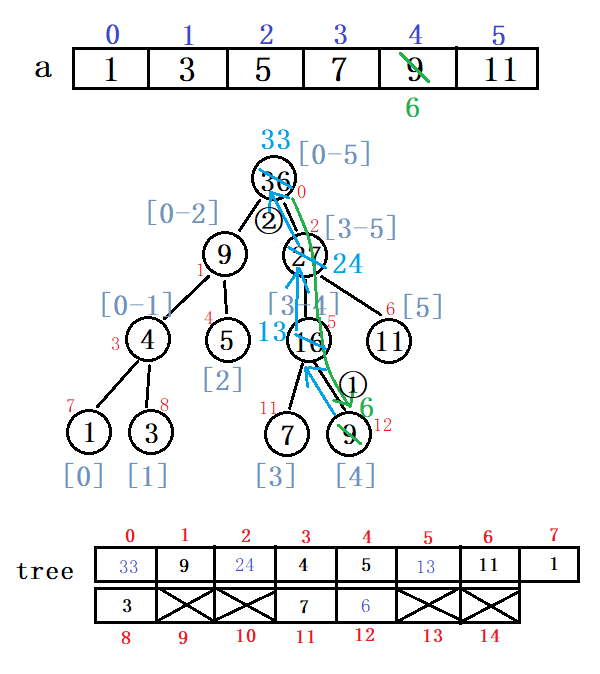
void update(int a[], int tree[], int node, int start, int end, int x, int val){
//找到a[x],修改值
if (start == end){
a[x] = val;
tree[node] = val;
}
else {
int mid = (start + end) / ;
int left = * node + ;
int right = * node + ;
if (x >= start && x <= mid) {//如果x在左分支
update(a, tree, start, mid, x, val);
}
else {//如果x在右分支
update(a, tree, right, mid+, end, x, val);
}
//向上更新值
tree[node] = tree[left] + tree[right];
}
}
在主函数中调用:
//把a[x]改成6
update(a, tree, , , size-, , );
运行结果:
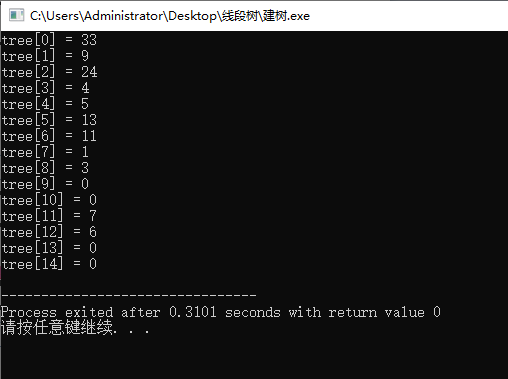
query操作:
- 向下依次寻找包含在目标区间中的区间,并累加。
- 与建树的函数相比,query函数增加了两个参数L,Rl,即把求a的区间[L,R]的和。
例:求a[2]+a[3]+...+a[5]的值(代码实现)
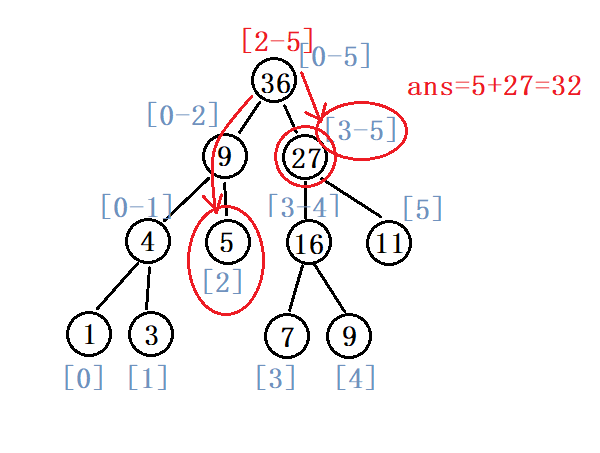
int query(int a[], int tree[], int node, int start, int end, int L,int R){
//若目标区间与当时区间没有重叠,结束递归返回0
if (start > R || end < L){
return ;
}
//若目标区间包含当时区间,直接返回节点值
else if (L <=start && end <= R){
return tree[node];
}
else {
int mid = (start + end) / ;
int left = * node + ;
int right = * node + ;
//计算左边区间的值
int sum_left = query(a, tree, left, start, mid, L, R);
//计算右边区间的值
int sum_right = query(a, tree, right, mid+, end, L, R);
//相加即为答案
return sum_left + sum_right;
}
}
在主函数中调用:
//求区间[2,5]的和
int ans = query(a, tree, , , size-, , );
printf("ans = %d", ans);
运行结果:
最后,献上完整的代码:
#include<bits/stdc++.h>
using namespace std; const int N = ; int a[] = {, , , , , };
int size = ;
int tree[N] = {}; //建立范围为a[start]~a[end]
void build(int a[], int tree[], int node/*当前节点*/, int start, int end){
//递归边界(即遇到叶子节点时)
if (start == end) {
//直接存储a数组中的值
tree[node] = a[start];
} else {
//将建立的区间分成两半
int mid = (start + end) / ; int left = * node + ;//左子节点的下标
int right = * node + ;//右子节点的下标 //求出左子节点的值(即从节点left开始,建立范围为a[start]~a[mid])
build(a, tree, left, start, mid);
//求出右子节点的值(即从节点right开始,建立范围为a[start]~a[mid])
build(a, tree, right, mid+, end); //当前节点的职位左子节点的值加上右子节点的值
tree[node] = tree[left] + tree[right];
}
} void update(int a[], int tree[], int node, int start, int end, int x, int val){
//找到a[x],修改值
if (start == end){
a[x] = val;
tree[node] = val;
} else {
int mid = (start + end) / ; int left = * node + ;
int right = * node + ; if (x >= start && x <= mid) {//如果x在左分支
update(a, tree, left, start, mid, x, val);
}
else {//如果x在右分支
update(a, tree, right, mid+, end, x, val);
} //向上更新值
tree[node] = tree[left] + tree[right];
}
} //求a[L]~a[R]的区间和
int query(int a[], int tree[], int node, int start, int end, int L,int R){
//若目标区间与当时区间没有重叠,结束递归返回0
if (start > R || end < L){
return ;
} //若目标区间包含当时区间,直接返回节点值
else if (L <=start && end <= R){
return tree[node];
} else {
int mid = (start + end) / ; int left = * node + ;
int right = * node + ; //计算左边区间的值
int sum_left = query(a, tree, left, start, mid, L, R);
//计算右边区间的值
int sum_right = query(a, tree, right, mid+, end, L, R); //相加即为答案
return sum_left + sum_right;
}
} int main(){
//从根节点(即节点0)开始建树,建树范围为a[0]~a[size-1]
build(a, tree, , , size-); for(int i = ; i <= ; i ++)
printf("tree[%d] = %d\n", i, tree[i]);
printf("\n"); //把a[x]改成6
update(a, tree, , , size-, , ); for(int i = ; i <= ; i ++)
printf("tree[%d] = %d\n", i, tree[i]);
printf("\n"); //求区间[2,5]的和
int ans = query(a, tree, , , size-, , );
printf("ans = %d", ans); return ;
}
运行结果:
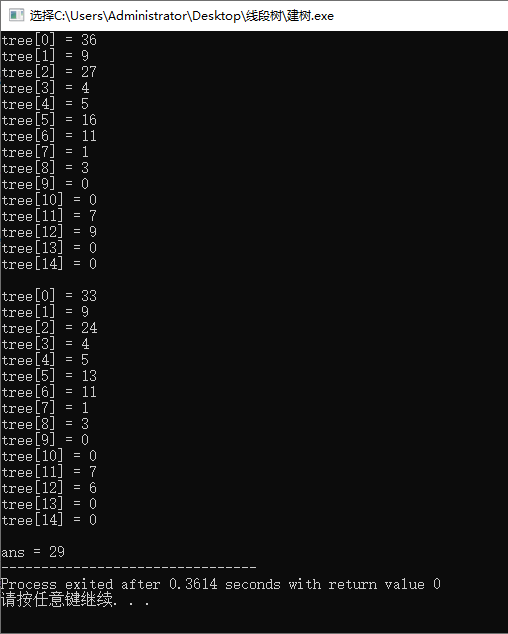
【数据结构】线段树(Segment Tree)的更多相关文章
- 『线段树 Segment Tree』
更新了基础部分 更新了\(lazytag\)标记的讲解 线段树 Segment Tree 今天来讲一下经典的线段树. 线段树是一种二叉搜索树,与区间树相似,它将一个区间划分成一些单元区间,每个单元区间 ...
- 线段树(Segment Tree)(转)
原文链接:线段树(Segment Tree) 1.概述 线段树,也叫区间树,是一个完全二叉树,它在各个节点保存一条线段(即“子数组”),因而常用于解决数列维护问题,基本能保证每个操作的复杂度为O(lg ...
- 【数据结构系列】线段树(Segment Tree)
一.线段树的定义 线段树,又名区间树,是一种二叉搜索树. 那么问题来了,啥是二叉搜索树呢? 对于一棵二叉树,若满足: ①它的左子树不空,则左子树上所有结点的值均小于它的根结点的值 ②若它的右子树不空, ...
- BZOJ.4695.最假女选手(线段树 Segment tree Beats!)
题目链接 区间取\(\max,\ \min\)并维护区间和是普通线段树无法处理的. 对于操作二,维护区间最小值\(mn\).最小值个数\(t\).严格次小值\(se\). 当\(mn\geq x\)时 ...
- 线段树(segment tree)
线段树在一些acm题目中经常见到,这种数据结构主要应用在计算几何和地理信息系统中.下图就为一个线段树: (PS:可能你见过线段树的不同表示方式,但是都大同小异,根据自己的需要来建就行.) 1.线段树基 ...
- 浅谈线段树 Segment Tree
众所周知,线段树是algo中很重要的一项! 一.简介 线段树是一种二叉搜索树,与区间树相似,它将一个区间划分成一些单元区间,每个单元区间对应线段树中的一个叶结点. 使用线段树可以快速的查找某一个节点在 ...
- 线段树 Interval Tree
一.线段树 线段树既是线段也是树,并且是一棵二叉树,每个结点是一条线段,每条线段的左右儿子线段分别是该线段的左半和右半区间,递归定义之后就是一棵线段树. 例题:给定N条线段,{[2, 5], [4, ...
- 第二十九篇 玩转数据结构——线段树(Segment Tree)
1.. 线段树引入 线段树也称为区间树 为什么要使用线段树:对于某些问题,我们只关心区间(线段) 经典的线段树问题:区间染色,有一面长度为n的墙,每次选择一段墙进行染色(染色允许覆盖),问 ...
- 算法手记 之 数据结构(线段树详解)(POJ 3468)
依然延续第一篇读书笔记,这一篇是基于<ACM/ICPC 算法训练教程>上关于线段树的讲解的总结和修改(这本书在线段树这里Error非常多),但是总体来说这本书关于具体算法的讲解和案例都是不 ...
- ACM数据结构-线段树
1.维护区间最大最小值模板(以维护最小值为例) #include<iostream> #include<stdio.h> #define LEN 11 #define MAX ...
随机推荐
- C语言学习书籍推荐《C语言入门经典(第4版)》
霍顿 (Ivor Horton) (作者), 杨浩 (译者) <C语言入门经典(第4版)>的目标是使你在C语言程序设计方面由一位初学者成为一位称职的程序员.读者基本不需要具备任何编程知识, ...
- python输出带颜色详解
书写格式: 开头部分:\033[显示方式;前景色;背景色m + 结尾部分:\033[0m 注意:开头部分的三个参数:显示方式,前景色,背景色是可选参数,可以只写其中的某一个:另外由于 ...
- 数据结构-堆栈和队列最简单的实现(Python实现)
OK,上篇博客我们介绍了双向链表以及代码实现,这篇文章我们来学习堆栈和队列. 队.栈和链表一样,在数据结构中非常基础一种数据结构,同样他们也有各种各样.五花八门的变形和实现方式.但不管他们形式上怎么变 ...
- 搭建Spring Initializr服务器
前言 按照网上很多教程,出错特别多.首先是GitHub和maven仓库的网络环境比较差,踩了很多坑:其次是SpringInitializr更新迭代几个版本,0.7.0我也没能弄成功.索性就用了旧版本0 ...
- CSDN怎么一键转载别人的博客
在参考"如何快速转载CSDN中的博客"后,由于自己不懂html以及markdown相关知识,所以花了一些时间来弄明白怎么转载博客,以下为转载CSDN博客步骤和一些知识小笔记. 参考 ...
- C++内存泄漏及检测工具详解
#include "stdafx.h" #ifdef _DEBUG #define DEBUG_CLIENTBLOCK new( _CLIENT_BLOCK, __FILE__, ...
- c语言进阶6-指针
指针是c语言的一个重要组成部分 是c语言的核心.精髓所在,用好指针可以在c语言编程中起到事半功倍的效果.一方面,可以提高程序的编译效率和执行速度以及实现动态的存储分配:另一方面,使用指针可使程序更灵活 ...
- jmter快速安装
一.简介 Apache JMeter是Apache组织开发的基于Java的压力测试工具,用于接口和压力测试,所以前提是一定更要安装jdk. 二.下载安装 下载:官网下载 下载完成后运行包里的jmete ...
- C#编程之JSON序列化与反序列化
1.在C#管理NuGet程序包中添加Json.NET 2.C#将对象序列化成JSON字符串 模型类1 /// <summary> /// JSON字符串模型.是否出错 /// </s ...
- CIDR的介绍
CIDR的介绍: CIDR(Classless Inter-Domain Routing,无类域间路由选择)它消除了传统的A类.B类和C类地址以及划分子网的概念,因而可以更加有效地分配IPv4的地址空 ...
