Perl寻路A*算法实现

　　A*算法；A*（A-Star)算法是一种静态路网中求解最短路径最有效的直接搜索方法。估价值与实际值越接近，估价函数取得就越好。

　　公式表示为： f(n)=g(n)+h(n),其中 f(n) 是从初始点经由节点n到目标点的估价函数，g(n) 是在状态空间中从初始节点到n节点的实际代价，h(n) 是从n到目标节点最佳路径的估计代价。

　　保证找到最短路径（最优解的）条件，关键在于估价函数f(n)的选取：估价值h(n)<= n到目标节点的距离实际值，这种情况下，搜索的点数多，搜索范围大，效率低。但能得到最优解。并且如果h(n)=d(n)，即距离估计h(n)等于最短距离，那么搜索将严格沿着最短路径进行， 此时的搜索效率是最高的。如果 估价值>实际值,搜索的点数少，搜索范围小，效率高，但不能保证得到最优解。

　　创建两个表，OPEN表保存所有已生成而未考察的节点，CLOSED表中记录已访问过的节点。算起点的估价值;将起点放入OPEN表;保存路径，即从终点开始，每个节点沿着父节点移动直至起点，这就是你的路径。

　　算法伪码：

while(OPEN!=NULL)
{
    从OPEN表中取估价值f(n)最小的节点n;
    if(n节点==目标节点)
        break;
    for(当前节点n的每个子节点X)
    {
        算X的估价值;
        if(XinOPEN)
            if(X的估价值小于OPEN表的估价值)
            {
                把n设置为X的父亲;
                更新OPEN表中的估价值;//取最小路径的估价值
            }
        if(XinCLOSE)
            continue;
        if(Xnotinboth)
        {
            把n设置为X的父亲;
            求X的估价值;
            并将X插入OPEN表中;//还没有排序
        }
    }//endfor
    将n节点插入CLOSE表中;
    按照估价值将OPEN表中的节点排序;//实际上是比较OPEN表内节点f的大小，从最小路径的节点向下进行。
}//endwhile(OPEN!=NULL)

　　以上摘自百度百科，以下将用Perl语言实现:　　

　　1、建立路径数组，下标即是步数，并使用匿名哈希保存坐标点、开销、到目的地开销、实际开销、父节点等信息，数据结构如下：

　　　　path[step]={ coordinate=>[y,x],

　　　　　　　　　　　cost=>0,

　　　　　　　　　　　next_cost=>(y-end.y)+(x-end.x),

　　　　　　　　　　　previous=>path[step-1],

　　　　　　　　　　　actual_cost=>cost+next_cost }

　　2、另一个数组，下标即是坐标点，指向的匿名哈希存放OPEN、CLOSE、前一节点的状态，如: arr[y][x]->{point}，方便回退时能直接获取到上一步的坐标点和状态，数据结构如下：

　　　　arr[y][x]={ flag=>0,

　　　　　　　　　　point=>arr[y-1][x-1] }

　　数据结构设计好后，根据上面的伪代码实现还是比较容易：

use strict;
use List::Util;
use constant {WIDTH=>,HEIGHT=>,DEBUG=>,};
my @uldr=( ,[-,],[,-],[,],[,], );  # 上、左、下、右
my @bg=();
for(my $y=;$y<HEIGHT;$y++){
    for( my $x= ; $x<WIDTH ; $x++ ){
        if( $y ==  || $y == HEIGHT- ||
            $x ==  || $x == WIDTH-  ){
            $bg[$y][$x] = '*';
        }
        else{
            $bg[$y][$x] = ' ';
        }
    }
}  # 初始化迷宫

my @obstruction=( [,],[,],[,],[,],[,],[,],[,],[,],[,],[,],[,],[,], );  # 障碍物坐标
map{ $bg[ $obstruction[$_][] ][ $obstruction[$_][] ] = '#' } ..$#obstruction-1;
$bg[ $obstruction[][] ][ $obstruction[][] ] = '@';

@bg=( ['*','*','*','*','*','*','*','*','*','*','*','*',],
      ['*',' ',' ',' ','#',' ',' ',' ',' ',' ',' ','*',],
      ['*',' ','#',' ',' ',' ',' ',' ',' ',' ',' ','*',],
      ['*',' ','#',' ',' ',' ','#',' ',' ',' ',' ','*',],
      ['*',' ','#',' ',' ',' ','#','#','#','#','#','*',],
      ['*',' ',' ','#',' ',' ','#',' ',' ',' ',' ','*',],
      ['*',' ',' ',' ',' ',' ',' ',' ',' ',' ',' ','*',],
      ['*','*','*','*','*','*','*','*','*','*','*','*',],
      );
print @$_,"\n" foreach(@bg);
my @bg_ghost=();  # 0--未经过 1--已走 2--不可通过

print "-"x15,"\n";
sub caclulate_cost{
    my ($sp,$ep)=@_;
    return abs($sp->[] - $ep->[]) + abs($sp->[] - $ep->[]);
}
sub handle{
    my @path=();  # 存放步数的数组
    my $start=[ $obstruction[][] , $obstruction[][] ];  # 起点
    $start=[,];
    my $end=[ $obstruction[-][] , $obstruction[-][] ];  # 终点
    $end=[,];
    my ($step,$p_step,$p_gh)=(,'','');  # 步数、指向数组元素的指针、指向bg_ghost元素的指针

    $path[$step]={ coordinate=>[$start->[],$start->[]],
                   cost=>,
                   next_cost=>&caclulate_cost( $start,$end ),
                   previous=>,
                  };   # 每一步保存坐标、预计开销、到目的地距离、父节点，起点开销为0
    $path[$step]->{actual_cost}=$path[$step]->{cost} + $path[$step]->{next_cost};  # 实际开销
    $bg_ghost[ $start->[] ][ $start->[] ]->{point}='';   # 起点的父节点为空
    while(@path){
        $p_step=pop(@path);
        print "  step:$step,p_step:$p_step\n" if DEBUG;
        if( $p_step->{coordinate}->[] == $end->[] &&
            $p_step->{coordinate}->[] == $end->[] ){   # 到达目的地
            my @arr=('A'..'Z','a'..'z');
            my @temp=();
            while($p_step){
                push @temp,$p_step->{coordinate};
                $p_step=$p_step->{previous};   # 顺着父节点回溯，获取每个节点
            }
            @temp=reverse(@temp);
            foreach(..$#temp){
                $bg[ $temp[$_]->[] ][ $temp[$_]->[] ] = $arr[$_];
            }
            return ;
        }  # end if
        $step++;
        for(my $cnt=;$cnt<=;$cnt++){
            my $y= $p_step->{coordinate}->[]+$uldr[$cnt][] ;
            my $x= $p_step->{coordinate}->[]+$uldr[$cnt][] ;
            print "    ($p_step->{coordinate}->[0],$p_step->{coordinate}->[1])+($uldr[$cnt][0],$uldr[$cnt][1]),(y,x)=($y,$x)\n" if DEBUG;
            if( $y <  || $y > HEIGHT- || $x <  || $x > WIDTH- || $bg[$y][$x] eq '#' ){
                $bg_ghost[$y][$x]->{flag} =  ;  # 不可经过
            }
            if( ! $bg_ghost[$y][$x]->{flag} ){        # 未经过的
                $bg_ghost[$y][$x]->{flag}=;        # 设置已经过
                $bg_ghost[$y][$x]->{point}=$p_step; # 保存前一节点状态
                my $px={  coordinate=>[$y,$x],
                                   cost=>$p_step->{cost}+,
                                   next_cost=>&caclulate_cost( [$y,$x],$end ),
                                   previous=>$p_step,
                               };
                $px->{actual_cost}=$px->{cost} + $px->{next_cost};
                push @path,$px;
            }
            else{
                $p_gh=$bg_ghost[$y][$x]->{point};
                print "      p_gh:$p_gh\n" if DEBUG;
                if($p_gh && $p_step->{cost}+ < $p_gh->{cost} ){   # 如果当前开销较小
                    print "      $p_step->{cost},$p_gh->{cost}\n" if DEBUG;
                    $p_gh->{cost}=$p_step->{cost}+;    #
                    $p_gh->{previous}=$p_step;            # 将前一个节点设置为当前节点之父
                    $p_gh->{actual_cost}=$p_gh->{cost}+$p_gh->{next_cost};        # 更新前一节点开销
                }
            }
        }
        $bg_ghost[ $p_step->{coordinate}->[] ][ $p_step->{coordinate}->[] ]->{flag}=;  # 设置已经过
        @path=sort{$b->{actual_cost}<=>$a->{actual_cost}}@path;   # 排序，开销最小的放在最后
    }
    return ;
}
&handle;
print @$_,"\n" foreach(@bg);

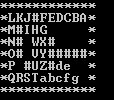
　　计算出来的最短路径：

　　　　

　　比较一下深度优先算法：