bzoj2839 集合计数 组合计数 容斥原理|题解

集合计数

题目描述

一个有N个元素的集合有2^N个不同子集（包含空集），现在要在这2^N个集合中取出若干集合（至少一个），使得它们的交集的元素个数为K，求取法的方案数，答案模1000000007。（是质数喔~）

输入格式

一行两个整数N,K

输出格式

一行为答案。

样例

样例输入

3 2

样例输出

6

数据范围与提示

样例说明

假设原集合为{A,B,C}

则满足条件的方案为：{AB,ABC},{AC,ABC},{BC,ABC},{AB},{AC},{BC}

数据说明

对于100%的数据，1≤N≤1000000；0≤K≤N；

题解

看到这个题我们很自然的想到答案是

$\binom{n}{k}*f(n-k)$

其中f（i）表示i个元素的2ⁱ个集合中，选出任意多集合使交集为空的方案数，但是一个集合都不选是不合法的

一个暴力算法

显然f（0）=1

设g（i，j）表示从i个元素的集合中，选出任意多集合使交集为k个的方案数

$g(i，j)=\binom{i}{j}*f(i-j)$

对于i>1    $f(i)=2^{2^i}-1-\sum\limits_{j=1}^{i}g(i,j)$

注意不能一个集合都不选，但可以选择集合中没有任何元素的集合来组成一个对集合的集合，这涉及到-1的位置

复杂度O（n²）  期望得分70

正解 容斥原理

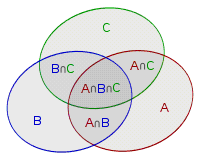
$f(n)=\sum\limits_{i=0}^{n}*(-1)^i*\binom{n}{i}*(2^{2^{n-i}}-1)$

集合A B C表示交集中含有 a，b，c的集合取法

C（n，i）表示从n个形如A B C的集合中取出i个，算出有多少种取法

这i个集合的交集则表示同时含有这i个元素

后一项则表示其他集合任意选取，但不能一个都不选的方案数

偶加奇减，则得到全集减去这几个集合的并集，得到f（i）

 #include<iostream>
 #include<cstdio>
 #define ll long long
 using namespace std;
 const int mod=1e9+;
 int n,k;
 ll js[],jsinv[];
 ll qpow(ll base,int y,int mo)
 {
     ll ans=;
     while(y)
     {
         if(y&) ans=ans*base%mo;
         base=base*base%mo;
         y>>=;
     }
     return ans;
 }
 void init()
 {
     js[]=;
     for(int i=;i<=n;i++) js[i]=js[i-]*i%mod;
     jsinv[n]=qpow(js[n],mod-,mod);
     for(int i=n-;i>=;i--) jsinv[i]=jsinv[i+]*(i+)%mod;
 }
 inline ll C(int n,int m)
 {
     return js[n]*jsinv[m]%mod*jsinv[n-m]%mod;
 }
 inline ll ask(int m)
 {
     ll ans=;
     for(int i=,u=;i<=m;i++,u=-u)
         ans=(ans+u*C(m,i)*(qpow(,qpow(,m-i,mod-),mod)-)%mod)%mod;
     return ans;
 }
 int main()
 {
     scanf("%d%d",&n,&k);
     init();
     printf("%lld\n",(ask(n-k)*C(n,k)%mod+mod)%mod);
     return ;
 }

另一种等价的方法

$ans=\binom{n}{k}*\sum\limits_{i=k}^{n}(-1)^{i-k}*\binom{n-k}{i-k}*(2^{2^{n-i}}-1)$

这种方法可以理解为固定一种组合，从其他集合中选取几个进行容斥

也能算出答案

 #include<iostream>
 #include<cstdio>
 #define ll long long
 using namespace std;
 const int mod=1e9+;
 int n,k;
 ll js[],jsinv[];
 ll qpow(ll base,int y,int mo)
 {
     ll ans=;
     while(y)
     {
         if(y&) ans=ans*base%mo;
         base=base*base%mo;
         y>>=;
     }
     return ans;
 }
 void init()
 {
     js[]=;
     for(int i=;i<=n;i++) js[i]=js[i-]*i%mod;
     jsinv[n]=qpow(js[n],mod-,mod);
     for(int i=n-;i>=;i--) jsinv[i]=jsinv[i+]*(i+)%mod;
 }
 inline ll C(int n,int m)
 {
     return js[n]*jsinv[m]%mod*jsinv[n-m]%mod;
 }
 int main()
 {
     scanf("%d%d",&n,&k);
     init();
     ll ans=;
     for(int i=k,u=;i<=n;i++,u=-u)
         ans=(ans+u*C(n-k,i-k)%mod*(qpow(,qpow(,n-i,mod-),mod)-)%mod)%mod;
     printf("%lld\n",(ans*C(n,k)%mod+mod)%mod);
     return ;
 }