一步一步编写AVL树

第一步：定义结构体

typedef struct Node{
    int d;        //data
    int h=;    //height
    struct Node* l=NULL;
    struct Node* r=NULL;
    Node(int d=):d(d){
    }
}Node; 

这个结构体和常规的二叉树结构体很相似。但是不同的是多了个属性“h”（height）。用这个属性来记录结点的高度，叶子结点为1，空结点为0 。

第二部：编写BST树的插入函数

Node* insert(Node* p,int v){
    Node * node=new Node(v);
    if(!p){
        return node;
    }
    if(v < p->d){    //左子树
        if(p->l){
            p->l=insert(p->l,v);
        }else{
            p->l=node;
        }
    }else{
        if(p->r){
            p->r=insert(p->r,v);
        }else{
            p->r=node;
        }
    }
//    setHeight(p);
    //平衡旋转代码 

    //end of 平衡旋转代码
    return p;
}

第三步：编写高度获取与设置的辅助函数

高度获取：

int getHeight(Node* node){
    if(node) return node->h;    //如果非空返回这个结点的height
    return ;                  //空节点的高度是0
}

高度设置：

void setHeight(Node* node){    //取左右子树高度的最大值，记得+1
    node->h=max(getHeight(node->l),getHeight(node->r))+;
}

第四步：编写平衡旋转函数

当左右子树的height相差为2时，就要调用平衡旋转函数进行旋转。一共有4种旋转模式：

（注：一下图片采用自博客：http://www.cnblogs.com/Camilo/p/3917041.html，如果侵权请联系我删除）

左子树左结点引起的不平衡：

Node* LL(Node* node){
    Node* re=node->l;
    node->l=re->r;
    re->r=node;
    setHeight(node);    //注意：先进行这一步。因为node是re的子结点，从下往上调整
    setHeight(re);
    return re;
}

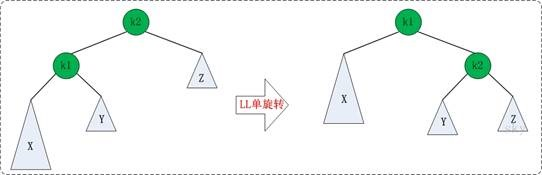
右子树右结点引起的不平衡：

Node* RR(Node* node){
    Node* re=node->r;
    node->r=re->l;
    re->l=node;
    setHeight(node);
    setHeight(re);
    return re;
}

（注：编写技巧是在LL函数的基础上，把所有的ｒ写成ｌ，把所有的ｌ写成ｒ，轮换对称思想）

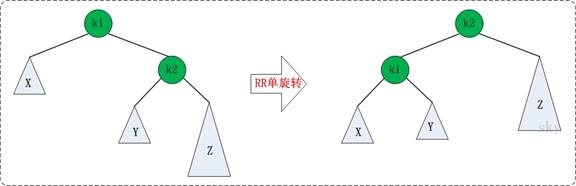
左子树右结点引起的不平衡：

Node* LR(Node* node){
    node->l=RR(node->l);
    node=LL(node);
    return node;
}

右子树左结点引起的不平衡：

Node* RL(Node* node){
    node->r=LL(node->r);
    node=RR(node);
    return node;
}

第五步：在BST树的插入函数中编写平衡旋转代码：

Node* insert(Node* p,int v){
    Node * node=new Node(v);
    if(!p){
        return node;
    }
    if(v < p->d){    //左子树
        if(p->l){
            p->l=insert(p->l,v);
        }else{
            p->l=node;
        }
    }else{
        if(p->r){
            p->r=insert(p->r,v);
        }else{
            p->r=node;
        }
    }
    setHeight(p);
    //平衡旋转代码
    if(getHeight(p->l)-getHeight(p->r)==){    //左子树不平衡
        if(getHeight(p->l->l)>getHeight(p->l->r)){//左结点不平衡
            p=LL(p);
        }else{        //右结点不平衡
            p=LR(p);
        }
    }
    if(getHeight(p->r)-getHeight(p->l)==){    //右子树不平衡
        if(getHeight(p->r->l)>getHeight(p->r->r)){//左结点不平衡
            p=RL(p);
        }else{        //右结点不平衡
            p=RR(p);
        }
    }
    //end of 平衡旋转代码
    return p;
}

打个OJ测试一下：1123. Is It a Complete AVL Tree

AC代码：

#include <stdio.h>
#include <queue>
#include <algorithm>

using namespace std;

typedef struct Node{
    int d;        //data
    int h=;    //height
    struct Node* l=NULL;
    struct Node* r=NULL;
    Node(int d=):d(d){
    }
}Node; 

int getHeight(Node* node){
    if(node) return node->h;    //如果非空返回这个结点的height
    return ;                  //空节点的高度是0
}

void setHeight(Node* node){    //取左右子树高度的最大值，记得+1
    node->h=max(getHeight(node->l),getHeight(node->r))+;
}

Node* LL(Node* node){
    Node* re=node->l;
    node->l=re->r;
    re->r=node;
    setHeight(node);    //注意：先进行这一步。因为node是re的子结点，从下往上调整
    setHeight(re);
    return re;
}

Node* RR(Node* node){
    Node* re=node->r;
    node->r=re->l;
    re->l=node;
    setHeight(node);
    setHeight(re);
    return re;
}

Node* LR(Node* node){
    node->l=RR(node->l);
    node=LL(node);
    return node;
}

Node* RL(Node* node){
    node->r=LL(node->r);
    node=RR(node);
    return node;
}

Node* insert(Node* p,int v){
    Node * node=new Node(v);
    if(!p){
        return node;
    }
    if(v < p->d){    //左子树
        if(p->l){
            p->l=insert(p->l,v);
        }else{
            p->l=node;
        }
    }else{
        if(p->r){
            p->r=insert(p->r,v);
        }else{
            p->r=node;
        }
    }
    setHeight(p);
    //平衡旋转代码
    if(getHeight(p->l)-getHeight(p->r)==){    //左子树不平衡
        if(getHeight(p->l->l)>getHeight(p->l->r)){//左结点不平衡
            p=LL(p);
        }else{        //右结点不平衡
            p=LR(p);
        }
    }
    if(getHeight(p->r)-getHeight(p->l)==){    //右子树不平衡
        if(getHeight(p->r->l)>getHeight(p->r->r)){//左结点不平衡
            p=RL(p);
        }else{        //右结点不平衡
            p=RR(p);
        }
    }
    //end of 平衡旋转代码
    return p;
}

int cnt=;

int main(){
//    freopen("I:\\pat\\树\\AVL\\1123_2.txt","r",stdin);
    int n,t;
    scanf("%d",&n);
    Node * root;
    for(int i=;i<n;i++){
        scanf("%d",&t);
        root=insert(root,t);
    }
    queue<Node*> q;
    q.push(root);
    bool findNull=;
    bool yes=;
    bool after=;
    while(!q.empty()){
        Node* t=q.front();
        q.pop();
        printf("%d",t->d);
        cnt++;
        if(cnt!=n)
            printf(" ");
        if(t->l){
            q.push(t->l);
            if(after) yes=;
        }
        else after=;
        if(t->r){
            q.push(t->r);
            if(after) yes=;
        }
        else after=;
    }
    puts("");
    puts(yes?"YES":"NO");
    return ;
}