QuantLib 金融计算——案例之普通欧式期权分析
如果未做特别说明,文中的程序都是 python3 代码。
QuantLib 金融计算——案例之普通欧式期权分析
载入 QuantLib 和其他包:
import QuantLib as ql
import numpy as np
import pandas as pd
print(ql.__version__)
1.15
概述
从金融工程中最简单的案例——“普通欧式期权公式法定价”入手,介绍 QuantLib 中期权分析的基本组件,以及如何将这些组件拼接成为一个完整的计算流程。
普通欧式期权公式法定价
采用《期权、期货及其他衍生产品(第 7 版)》第 17 章中的例子:
- 类型:普通欧式看涨期权
- 当前价格:49$
- 敲定价格:50$
- 无风险利率:5%
- 年化波动率:20%
- 期限:20 周
使用 BS 公式为上述期权定价,并计算希腊值。
1. 配置期权合约条款
# 配置日期计算条款
calendar = ql.UnitedStates(ql.UnitedStates.NYSE)
dayCounter = ql.Actual365Fixed(ql.Actual365Fixed.Standard)
todayDate = ql.Date(11, ql.July, 2019)
maturity = todayDate + ql.Period(20, ql.Weeks)
settlementDate = todayDate
# 配置期权参数
stock = 49
strike = 50
riskFreeRate = 0.05
volatility = 0.2
# 配置全局估值日期
ql.Settings.instance().evaluationDate = todayDate
2. 构建期权对象
# 配置行权条款
europeanExercise = ql.EuropeanExercise(maturity)
optionType = ql.Option.Call
payoff = ql.PlainVanillaPayoff(
type=optionType, strike=strike)
# 构建期权对象
europeanOption = ql.VanillaOption(
payoff=payoff,
exercise=europeanExercise)
3. 配置定价引擎
underlying = ql.SimpleQuote(stock)
underlyingH = ql.QuoteHandle(underlying)
# 无风险利率的期限结构
flatRiskFreeTS = ql.YieldTermStructureHandle(
ql.FlatForward(
settlementDate, riskFreeRate, dayCounter))
# 波动率的期限结构
flatVolTS = ql.BlackVolTermStructureHandle(
ql.BlackConstantVol(
settlementDate, calendar,
volatility, dayCounter))
# 构建 BS 过程
bsProcess = ql.BlackScholesProcess(
s0=underlyingH,
riskFreeTS=flatRiskFreeTS,
volTS=flatVolTS)
# 基于 BS 过程的公式定价引擎
pricingEngine = ql.AnalyticEuropeanEngine(
bsProcess)
europeanOption.setPricingEngine(pricingEngine)
4. 计算
# RESULTS
print("Option value =", europeanOption.NPV())
print("Delta value =", europeanOption.delta())
print("Theta value =", europeanOption.theta())
print("Theta perday =", europeanOption.thetaPerDay())
print("Gamma value =", europeanOption.gamma())
print("Vega value =", europeanOption.vega())
print("Rho value =", europeanOption.rho())
Option value = 2.395988448539984
Delta value = 0.5213970624832108
Theta value = -4.309457134907618
Theta perday = -0.011806731876459226
Gamma value = 0.06563585494066533
Vega value = 12.089225358769994
Rho value = 8.88039853654583
题外话:天数计算规则
上述例子中的计算结果和书中给出的结果略有出入,依经验判断,最有可能造成计算不一致的原因是“天数计算规则的不一致”。
详细来说,书中期权的期限是 20 周,作者认为 20 周等于 0.3846 年,可能的依据有:
- \(20 \times 7 / 364(\text{not } 365) \approx 0.3846\) (即 Actual/364)或
- \(20 \times 5(\text{weekday}) / [52(\approx 365/7)\times 5(\text{weekday})] \approx 0.3846\)
目前,QuantLib 中并不支持这两种天数计算规则。例子中出现的规则
Actual365Fixed(Actual365Fixed.Standard)认为 20 周等于 0.38356 年:print(dayCounter.yearFraction(settlementDate, maturity))
# 0.3835616438356164
对于期权来说,天数计算规则的影响可能微不足道,但是对于固定收益类金融工具及其衍生品来说,天数计算规则的选择至关重要,“失之毫厘,谬以千里”。
Quote 带来的便利
QuantLib 中有相当多的组件接受 Handle 类型的参数,而这些参数通常持有一个 Quote 类型的变量。借助“观察者模式”,用户修改 Quote 类型变量的值将会自动通知相关组件,并使其重新进行性计算,而无需再次构建一遍计算流程。对于某些用途来讲,这带来了相当大的便利。
# USE QUOTE
stock_array = np.arange(
start=30, stop=70, step=0.01)
NPV = np.array([np.nan] * len(stock_array))
delta = np.array([np.nan] * len(stock_array))
theta = np.array([np.nan] * len(stock_array))
# thetaPerDay = np.array([np.nan] * len(stock_array))
gamma = np.array([np.nan] * len(stock_array))
vega = np.array([np.nan] * len(stock_array))
rho = np.array([np.nan] * len(stock_array))
for i, v in enumerate(stock_array):
# 重置 Quote 对象的值
underlying.setValue(v)
# 无须再次配置计算流程,直接计算
NPV[i] = europeanOption.NPV()
delta[i] = europeanOption.delta()
theta[i] = europeanOption.theta()
# thetaPerDay[i] = europeanOption.thetaPerDay()
gamma[i] = europeanOption.gamma()
vega[i] = europeanOption.vega()
rho[i] = europeanOption.rho()
result = pd.DataFrame(
data=dict(
NPV=NPV,
delta=delta,
theta=theta,
# thetaPerDay=thetaPerDay,
gamma=gamma,
vega=vega, rho=rho),
index=stock_array)
result.plot(subplots=True)
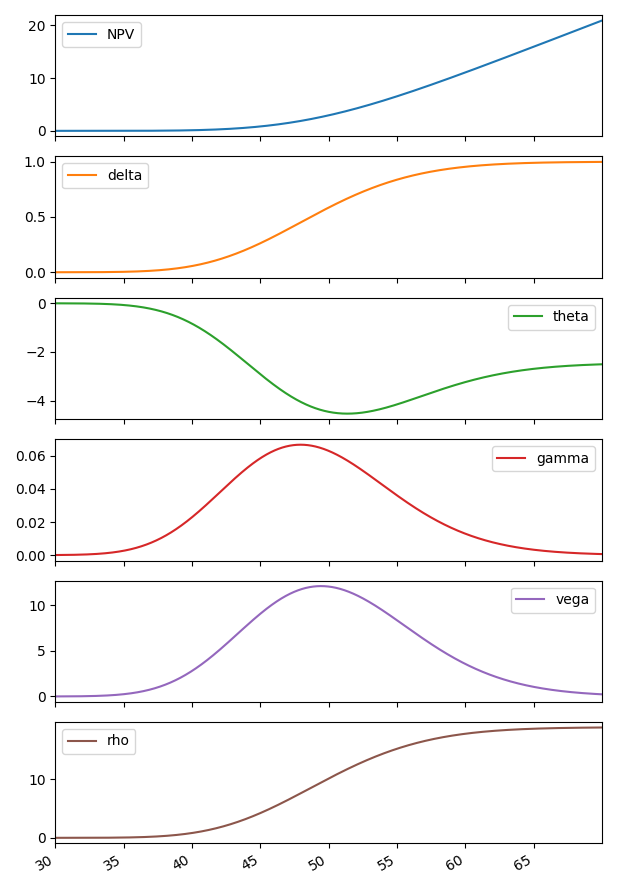
总结
下面用一副图显示上述例子中的若干变量如何汇聚成一个计算流程:
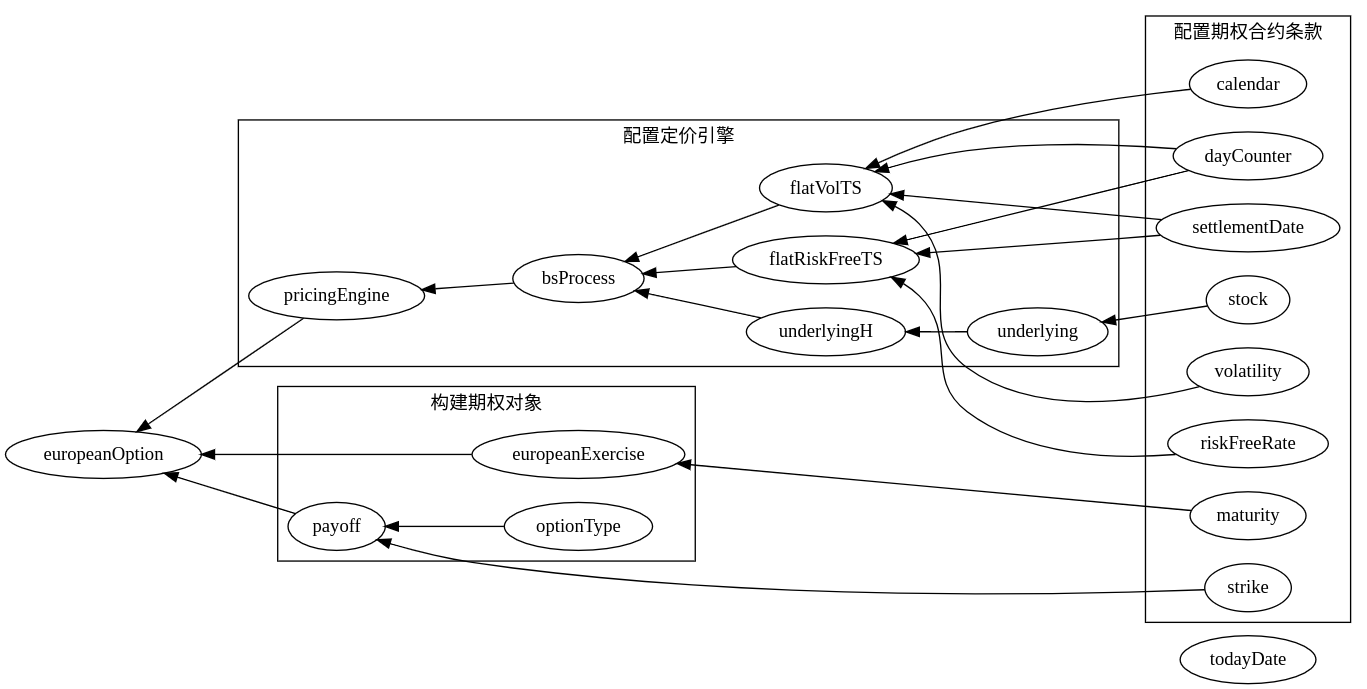
QuantLib 金融计算——案例之普通欧式期权分析的更多相关文章
- QuantLib 金融计算——QuantLib 入门
目录 QuantLib 金融计算--QuantLib 入门 简介 主要功能 安装与使用 学习指南 The HARD Way The EASY Way QuantLib 金融计算--QuantLib 入 ...
- QuantLib 金融计算——数学工具之数值积分
目录 QuantLib 金融计算--数学工具之数值积分 概述 常见积分方法 高斯积分 如果未做特别说明,文中的程序都是 Python3 代码. QuantLib 金融计算--数学工具之数值积分 载入模 ...
- QuantLib 金融计算
我的微信:xuruilong100 <Implementing QuantLib>译后记 QuantLib 金融计算 QuantLib 入门 基本组件之 Date 类 基本组件之 Cale ...
- QuantLib 金融计算——基本组件之 Currency 类
目录 QuantLib 金融计算--基本组件之 Currency 类 概述 构造函数 成员函数 如果未做特别说明,文中的程序都是 python3 代码. QuantLib 金融计算--基本组件之 Cu ...
- QuantLib 金融计算——高级话题之模拟跳扩散过程
目录 QuantLib 金融计算--高级话题之模拟跳扩散过程 跳扩散过程 模拟算法 面临的问题 "脏"的方法 "干净"的方法 实现 示例 参考文献 如果未做特别 ...
- QuantLib 金融计算——修复 BatesProcess 中的两个 Bug
QuantLib 金融计算--修复 BatesProcess 中的两个 Bug 我发现了 BatesProcess 中的两个 Bug: 基类 HestonProcess::factors 的返回值取决 ...
- QuantLib 金融计算——基本组件之 Date 类
目录 QuantLib 金融计算--基本组件之 Date 类 Date 对象的构造 一些常用的成员函数 一些常用的静态函数 为估值计算配置日期 如果未做特别说明,文中的程序都是 Python3 代码. ...
- QuantLib 金融计算——基本组件之 Calendar 类
目录 QuantLib 金融计算--基本组件之 Calendar 类 Calendar 对象的构造 一些常用的成员函数 自定义假期列表 工作日修正 如果未做特别说明,文中的程序都是 Python3 代 ...
- QuantLib 金融计算——基本组件之 DayCounter 类
目录 QuantLib 金融计算--基本组件之 DayCounter 类 DayCounter 对象的构造 一些常用的成员函数 如果未做特别说明,文中的程序都是 Python3 代码. QuantLi ...
随机推荐
- 我是如何一步步编码完成万仓网ERP系统的(八)产品库设计 4.品牌类别
https://www.cnblogs.com/smh188/p/11533668.html(我是如何一步步编码完成万仓网ERP系统的(一)系统架构) https://www.cnblogs.com/ ...
- 如何提升Web前端性能?
什么是WEB前端呢?就是用户电脑的浏览器所做的一切事情.我们来看看用户访问网站,浏览器都做了哪些事情:输入网址 –> 解析域名 -> 请求页面 -> 解析页面并发送页面中的资源请求 ...
- 个人项目-wc
个人项目-WC (C语言) 一.Github地址:https://github.com/Lin-J-F/WC 二.PSP表格 PSP2.1 Personal Software Process St ...
- Oracle 11.2.0.4打补丁
所需补丁及高版本opatch 上传后将p6880880_112000_Linux-x86-64.zip解压覆盖$ORACLE_HOME/OPatch目录即可 [oracle@localhost OPa ...
- AI-图像基础知识-01
目前人工智能Artificial Intelligence主要分为两大分支: 计算机视常见:Computer Vision,简称CV CV主要是研究如何让机器看懂世界的一种技术,通过各种光 ...
- 【Appium】Android 按键码
keycode也是appium很强大的功能,鉴于官网不翻墙无法打开,特此备忘. 电话键 KEYCODE_CALL 拨号键 5 KEYCODE_ENDCALL 挂机键 6 KEYCODE_HOM ...
- 用肘方法确定 kmeans 聚类中簇的最佳数量
说明: KMeans 聚类中的超参数是 K,需要我们指定.K 值一方面可以结合具体业务来确定,另一方面可以通过肘方法来估计.K 参数的最优解是以成本函数最小化为目标,成本函数为各个类畸变程度之和,每个 ...
- system.exit(int status)中status值不同时的区别
status为0时为正常退出程序,也就是结束当前正在运行中的java虚拟机. status为非0的其他整数(包括负数,一般是1或者-1),表示非正常退出当前程序. 可以明确的是,无论status是什么 ...
- K8s Helm安装配置入门
作为k8s现在主流的一种包部署方式,尽管不用,也需要进行一些了解.因为,它确实太流行了. 这一套太极拳打下来,感觉helm这种部署,目前还不太适合于我们公司的应用场景.它更适合需要手工编程各种yaml ...
- java.util.ConcurrentModificationException异常;java.util.ConcurrentModificationException实战
写代码遇到这个问题,很多博客文章都是在反复的强调理论,而没有对应的实例,所以这里从实例出发,后研究理论: 一.错误产生情况 1 .字符型 (1)添加 public static void main(S ...
