区间DP（超详细！！！）

一、问题

给定长为n的序列a[i]，每次可以将连续一段回文序列消去，消去后左右两边会接到一起，求最少消几次能消完整个序列，n≤500。

f[i][j]表示消去区间[i,j]需要的最少次数。

则;

若a[i]=a[j]，则还有。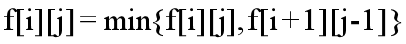

这里实际上是以区间长度为阶段的，这种DP我们通常称为区间DP。

区间DP的做法较为固定，即枚举区间长度，再枚举左端点，之后枚举区间的断点进行转移。

二、概念

区间类型动态规划是线性动态规划的拓展，它在分阶段划分问题时，与阶段中元素出现的顺序和由前一阶段的哪些元素合并而来有很大的关系。（例：f[i][j]=f[i][k]+f[k+1][j]）

区间类动态规划的特点：

• 合并：即将两个或多个部分进行整合。
• 特征：能将问题分解成为两两合并的形式。
• 求解：对整个问题设最优值，枚举合并点，将问题分解成为左右两个部分，最后将左右两个部分的最优值进行合并得到原问题的最优值。

三、例题

【例题一】石子合并：

【问题描述】

将n(1≤n≤200)堆石子绕圆形操场摆放，现要将石子有次序地合并成一堆。规定每次只能选相邻的两堆石子合并成新的一堆，并将新的一堆的石子数，记为该次合并的得分。 (1)选择一种合并石子的方案，使得做n-1次合并，得分的总和最小。 (2)选择一种合并石子的方案，使得做n-1次合并，得分的总和最大。

【样例输入】

4

4 5 9 4

【样例输出】

43

54

---

贪心解法：

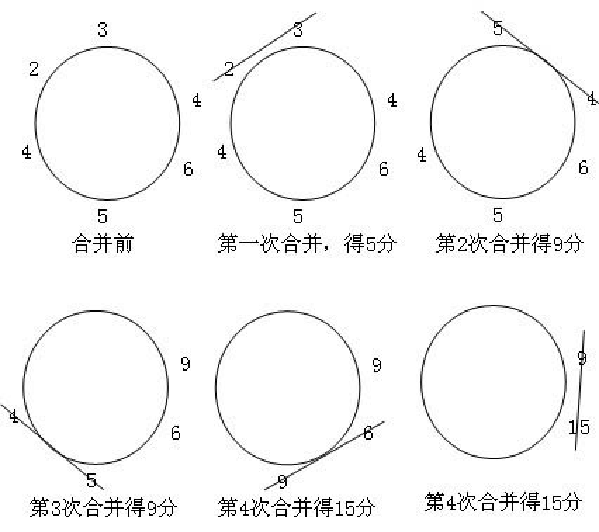
贪心共62分☝

正解共61分☟

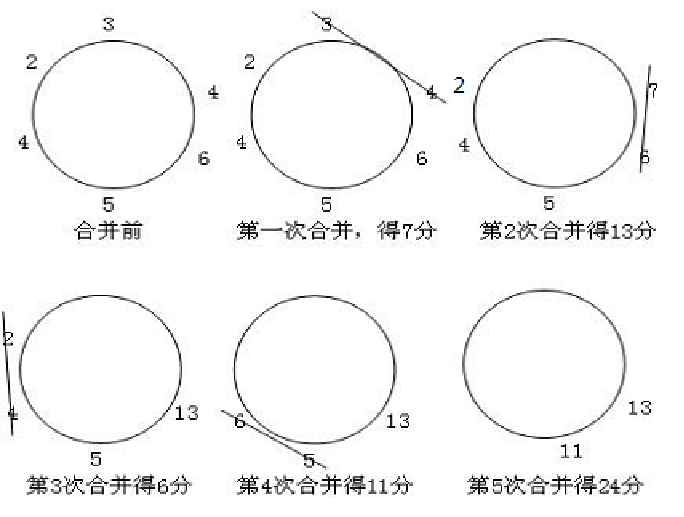
【思路点拨】

无环正解： 对应到动态规划中,就是两个长度较小的区间上的信息向一个更长的区间发生了转移,划分点k就是转移的决策，区间长度len就是DP的阶段。根据动态规划“选择最小的能覆盖状态空间的维度集合”的思想,可以只用左、右端点表示DP的状态。

sum[i]：从第1堆到第i堆石子数总和。

Fmax[i][j]：将从第i堆石子合并到第j堆石子的最大得分；

Fmin[i][j]：将从第i堆石子合并到第j堆石子的最小得分；

初始条件：Fmax[i][i]=0，Fmin[i][i]=INF

则状态转移方程为：（其中i<=k<j）

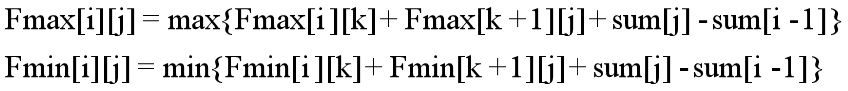
时间复杂度为。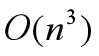

【环的处理】破环成链

注意到：题目中石子是围成一个圈，而不是一条线。

• 方法1：由于石子堆是围成一个圈，因此我们可以枚举分开的位置，首先将这个圈转化为链，因此要做n次，这样时间复杂度为 。
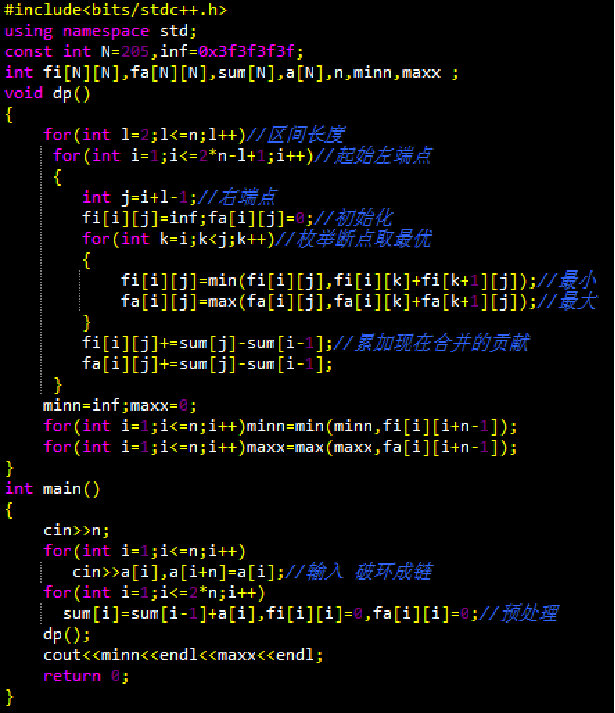
• 方法2：将这条链延长2倍，扩展成2n-1堆，其中第1堆与n+1堆完全相同，第i堆与n+i堆完全相同，这样只要对这2n堆动态规划后，枚举f(1,n),f(2,n+1),…,f(n,2n-1)取最优值即可。时间复杂度为 ,如下图：

【例题二】凸多边形的划分：

【问题描述】

给定一个具有N(N≤50)个顶点(从1到N编号)的凸多边形，每个顶点的权均是一个正整数。问：如何把这个凸多边形划分成N-2个互不相交的三角形，使得这些三角形顶点的权的乘积之和最小？

【输入示例】

5

121 122 123 245 231

【输出示例】

12214884

---

【题目分析】

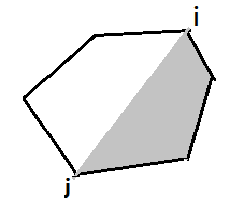
如果我们按顺时针将顶点编号，从顶点i到顶点j的凸多边形表示为如下图：

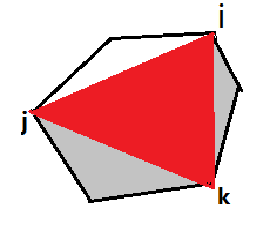
设f[i][j](i<j)表示从顶点i到顶点j的 凸多边形三角剖分后所得到的最大乘积，当 前我们可以枚举点k，考虑凸多边形(i,j)中 剖出三角形(i,j,k)，凸多边形(i,k)， 凸多边形(k,j)的最大乘积和。我们可以得到 动态转移方程：(1<=i<k<j<=n)

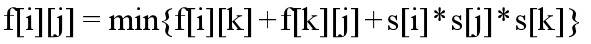
初始条件：f[i][i+1]=0； 目标状态：f[1][n]；

时间复杂度为：。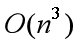

但我们可以发现,由于这里为乘积之和，在输入数据较大时有可能超过长整形范围，所以还需用高精度计算。

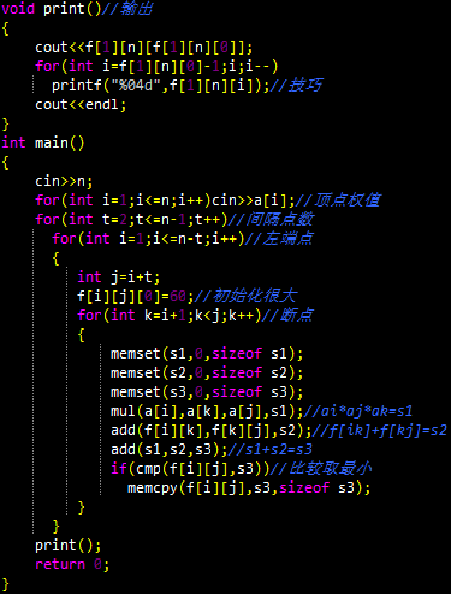
【总结】

基本特征：将问题分解成为两两合并的形式。

解决方法：对整个问题设最优值，枚举合并点，将问题分解成为左右两个部分，再将左右两个部分的最优值进行合并得到原问题的最优值。

设i到j的最优值，枚举剖分（合并）点，将(i,j)分成左右两区间，分别求左右两边最优值，如下图：

状态转移方程的一般形式如下：