leetcode-887-三维形体投影面积

题目描述：

在 N * N 的网格中，我们放置了一些与 x，y，z 三轴对齐的 1 * 1 * 1 立方体。

每个值 v = grid[i][j] 表示 v 个正方体叠放在单元格 (i, j) 上。

现在，我们查看这些立方体在 xy、yz 和 zx 平面上的投影。

投影就像影子，将三维形体映射到一个二维平面上。

在这里，从顶部、前面和侧面看立方体时，我们会看到“影子”。

返回所有三个投影的总面积。

示例 1：

输入：[[2]]
输出：5

示例 2：

输入：[[1,2],[3,4]]
输出：17
解释：
这里有该形体在三个轴对齐平面上的三个投影(“阴影部分”)。

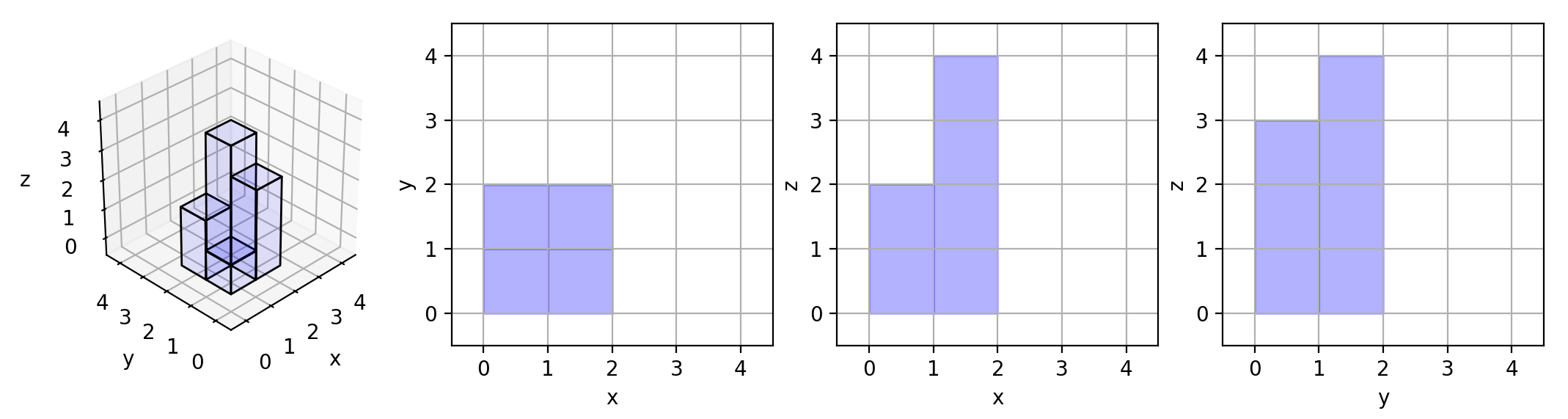
示例 3：

输入：[[1,0],[0,2]]
输出：8

示例 4：

输入：[[1,1,1],[1,0,1],[1,1,1]]
输出：14

示例 5：

输入：[[2,2,2],[2,1,2],[2,2,2]]
输出：21

提示：

• 1 <= grid.length = grid[0].length <= 50
• 0 <= grid[i][j] <= 50

要完成的函数：

int projectionArea(vector<vector<int>>& grid)

说明：

1、这道题给定一个二维的vector，记为grid，grid[i][j]表示在网格坐标为(i，j)的点上有grid[i][j]个立方体，每个立方体为1*1*1的体积。

要求从上方看下来，从前面看过去，从侧面看过去，从这三个方向看过去得到的投影面积之和是多少。

2、这是一道初中的数学题目吧？只不过我们现在用程序来自动化地完成运算，需要抽象出统一的规则。

①从上面看下来，这个好办，grid这个二维vector中有多少个不为0的元素，从上方看下来的投影面积就是多少。

比如grid为[[1,2],[3,4]]，图形如题目描述中所示，有四个不为0的元素，所以上方看下来的投影面积是4。

②从前面看过去，这个也不难，比如[[1,2],[3,4]]，我们说第一行第一列的元素是1，第一行第二列的元素是2，那么第一行我们最终能看到的投影面积就是2了，也就是取个最大值。

第二行第一列的元素是3，第二行第二列的元素是4，那么第二行我们最终能看到的投影面积也就是4了，也是取个最大值。

所以从前面看过去的投影面积，就是每一行的元素最大值的和。

③同理，从侧面看过去，这时候我们要取每一列的最大值了，最后再把每一列的最大值相加，就是我们要的侧面投影面积。

所以，代码如下：（附详解）

    int projectionArea(vector<vector<int>>& grid)
    {
        int hang=grid.size(),lie=grid[0].size(),shang=0,max1,qian=0,ce=0;
        for(int i=0;i<hang;i++)//按行读取
        {
            max1=0;
            for(int j=0;j<lie;j++)
            {
                if(grid[i][j])//如果这个元素不为0
                    shang++;//那么shang加1
                max1=max(max1,grid[i][j]);//取每一行的最大值
            }
            qian+=max1;//把每一行的最大值相加，存储在qian里面
        }
        for(int j=0;j<lie;j++)//按列读取
        {
            max1=0;
            for(int i=0;i<hang;i++)
            {
                max1=max(max1,grid[i][j]);//取每一列的最大值
            }
            ce+=max1;//把每一列的最大值相加，存储在ce里面
        }
        return shang+qian+ce;//最终返回三个投影面积相加的和
    }

上述代码实测8ms，因为总提交次数不足，所以还没有击败的百分比。