[SD2015]序列统计——solution

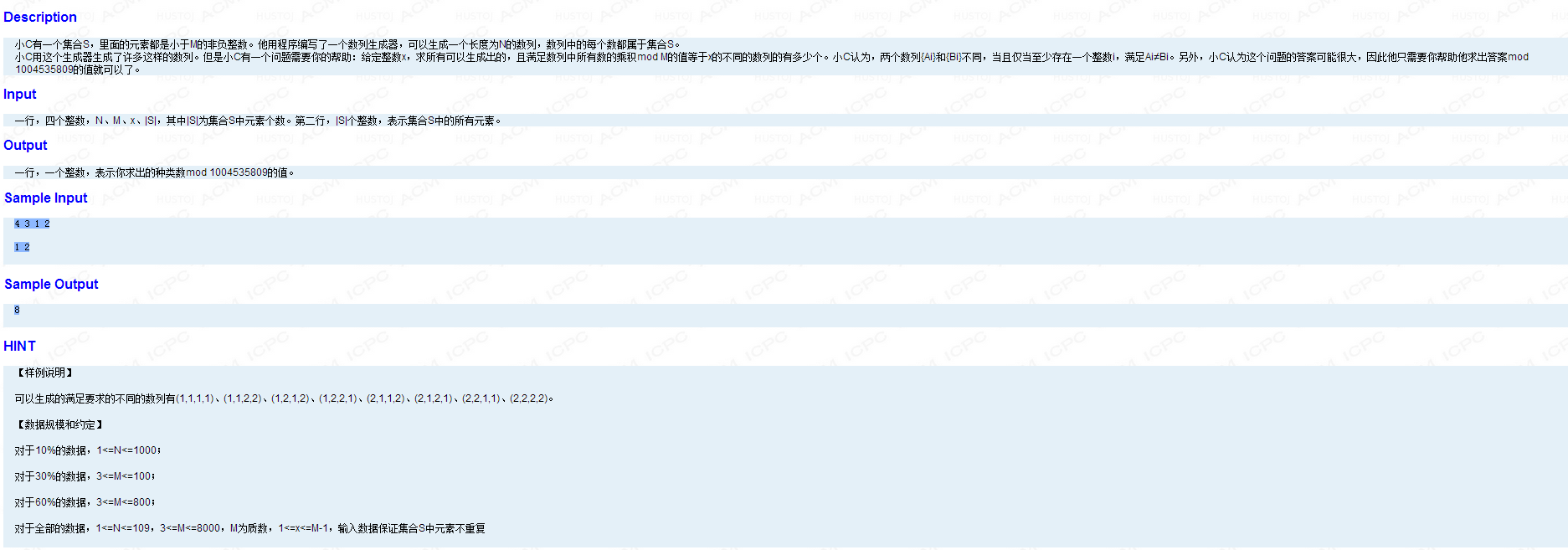
http://www.lydsy.com/JudgeOnline/problem.php?id=3992

---

---

很容易得出DP方程：

f[i][c]=f[i-1][a]*f[1][b]①

其中a*b%M=c

f第一位为当前数列长度，第二维为当前数列模M意义下的乘积

考虑从一开始就剔除第二维为0的情况——把它单独考虑，一来她好算，二来她不影响其他结果

若将f[i-1][a]展开；

则:

$$f[i][c]=\sum_{a_1=1}^M\sum_{a_2=1}^M...\sum_{a_i=1}^M([\Pi_{j=1}^ia_j(mod)M=c]\Pi_{j=1}^if[1][a_j])$$②

把f[1]的所有第二维取值得出的结果构造为多项式，记为$f_1(x)$

$$f_1(x)=map[0]x^0+map[1]x^1+map[2]x^2...map[m-1]x^{m-1}$$③

其中，map[i]为i数字在S中出现的次数，同样的，map[i]=f[1][i]

于是：

$$f_i(x)=\sum_{j=1}^{m-1}a_{i,j}*x^j$$④

其中$$a_{i,j}=\sum_{x=kj}\sum_{d|x}a_{i-1,d}*a_{1,{x \over d}}$$

当然$a_{x,y}=f[x][y]$

于是发现①，是多项式在模意义下的狄利克雷卷积；

而②，则是其在模意义下的狄利克雷卷积的乘幂

然而这个东西不能快速运算；

尝试转换这些式子；

看①，发现c取值在1到M-1之间，而$g^x$（其中g为M的原根）在x取0到M-2时可取遍1到M-1

不妨依此改写①

设$g^{e_x}=x$

$$f[i][g^{e_c}]=f[i-1][g^{e_a}]*f[1][g^{e_b}],e_c=(e_a+e_b)(mod)(M-1)$$

$$ff[i][e_c]=ff[i-1][e_a]*f[1][e_b],e_c=(e_a+e_b)(mod)(M-1)$$⑤

ff与f同构，求f[i][x]等价于求ff[i][e_x];

于是发现⑤，是多项式在模意义下的卷积；

NTT计算，加多项式取模；

如果把ff写成类似f的②的形式，则他是多项式在模意义下的卷积的乘幂；

快速幂优化

总效率$O(M*log_2M*log_2N)$

代码如下：

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cstdlib>
#include<cmath>
#define LL long long
using namespace std;
const LL mod=;
int N,M,X,S,len;
int rat[],map[],b[];
LL a[],ans[],g[],aa[];
LL Sqr_num(LL ,int );
void get_b(int );
void Sqr(int );
void pol_mul(LL a[],LL b[]);
int get_len(int );
void ra(LL f[]);
void NTT(LL f[],int t);
int main(){
    int i,j,k;
    scanf("%d%d%d%d",&N,&M,&X,&S);
    for(i=;i<=S;i++){
        scanf("%d",&j);
        map[j]++;
    }
    if(X==){
        printf("%lld",(Sqr_num(S,N)+mod-Sqr_num(S-map[],N))%mod);
        return ;
    }
    get_b(M);M--;
    for(i=;i<=M;i++)
        a[b[i]%(M)]=map[i]%mod;
    Sqr(N);
    printf("%lld",ans[b[X]%M]);
    return ;
}
LL Sqr_num(LL x,int n){
    LL ret=;
    while(n){
        if(n&)(ret*=x)%=mod;
        n>>=;(x*=x)%=mod;
    }
    return ret;
}
void get_b(int p){
    int i,j,f=,ij,g;
    for(i=;i<p;i++){
        ij=;f=;
        for(j=;j<p;j++){
            (ij*=i)%=p;
            if(j!=p-&&ij%p==)
                break;
            else
                if(j==p-&&ij%p==)
                    f=;
            }
        if(f){
            g=i;break;
        }
    }
    ij=;
    for(i=;i<p;i++){
        (ij*=g)%=p;
        b[ij]=i;
    }
}
void Sqr(int n){
    int i,fl=;
    len=get_len(M);
    rat[]=;
    for(i=;i<len;i++)
        rat[i]=rat[i>>]>>|((i&)*(len>>));
    while(n){
        if(n&){
            if(!fl){
                for(i=;i<M;i++)ans[i]=a[i];
                fl=;
            }
            else
                pol_mul(ans,a);
        }
        n>>=;
        for(i=;i<M;i++)
            aa[i]=a[i];
        pol_mul(a,aa);
    }
}
void pol_mul(LL a[],LL b[]){
    int i,j,k;
    for(i=M;i<len;i++)
        a[i]=,b[i]=;
    NTT(a,);NTT(b,);
    for(i=;i<len;i++)
        a[i]=a[i]*b[i]%mod;
    NTT(a,-);NTT(b,-);
    for(i=;i<M;i++)
        a[i]=(a[i]+a[i+M])%mod;
}
int get_len(int n){
    int ret=;
    while(ret<(n<<))ret<<=;
    return ret;
}
void ra(LL f[]){
    int i;
    for(i=;i<len;i++)
        if(rat[i]>i)
            swap(f[i],f[rat[i]]);
}
void NTT(LL f[],int t){
    int i,j,k,lim;
    int f0,f1;
    ra(f);
    for(k=;k<=len;k<<=){
        lim=k>>;
        g[]=;
        g[]=Sqr_num(,t>?(mod-)/k:mod--(mod-)/k);
        for(i=;i<lim;i++)
            g[i]=g[i-]*g[]%mod;
        for(i=;i<len;i+=k){
            for(j=i;j<i+lim;j++){
                f0=f[j];f1=g[j-i]*f[j+lim]%mod;
                f[j]=(f0+f1)%mod;f[j+lim]=(f0-f1+mod)%mod;
            }
        }
    }
    if(t<){
        LL inv=Sqr_num(len,mod-);
        for(i=;i<len;i++)
            (f[i]*=inv)%=mod;
    }
}