【文文殿下】Manache算法-学习笔记

Manache算法

　　定义：是一个判断回文子串的算法，我们结合例题解释：

　　　　　　　　题目：给定一个长度为 n 的字符串 S，求其最长回文子串 一个字符串是回文的，当且仅当反转后的串与原串完全相等

　　　分析：对于这个题目，有三种主流思路:

　　　　　　　　一：Hash+二分

　　　　　　　　　　　　计算字符串的前缀hash值

　　　　　　　　　　　　枚举中点，二分回文字串的长度

　　　　　　　　　　　　时间复杂度：$O(nlogn)$

　　　　　　　　　　二：回文自动机

　　　　　　　　　复杂度是线性的,但是编程复杂度极高，思维难度极高。

　　　　　　　　　　三：Manache算法

　　　　　　　复杂度是线性的，思维难度低，编程难度低

---

讲解Manache方法

　　　　　　对于Manache算法，我们先考虑朴素做法：枚举回文串中心，然后向两边扩展，这样的复杂度是$O(N^2)$的，

　　　　　　但是类比KMP算法，我们在朴素算法中，没有考虑到已经计算的部分对于之后结果的贡献，朴素方法的突破口就在这里了。

　　　　　　考虑优化：由于回文串长度分奇偶，有点麻烦，所以，我们考虑在每个字符中间插入一个'#'字符，来保证字符串的奇性。特别的，在字符串前两个字符，插入\$和#,对于\$的作用是：防止数组越界，既下文代码中的whie()函数，来确保其遇到字符串开头立即停止（因为对于$字符，其为唯一的，不可能有字符与其匹配）。

　　　　　　我们引入辅助数组$len[i]$ 来表示以$i$为中心，最大回文串的半径，显然的，对于每一个$len[i]$，$len[i]-1$就是原来回文串的长度，我们结合一个样例来说明：

　　　　　　原字符串：$   #   A   #   B   #   A   #   A   #    B    #

　　　　　　$len$数组　 1   1   2    1   4    1   2     2   2    1   2    1

　　　　　　原来的最长回文串是$3$ 也就是$len[4]-1$ （从0开始标号）。

　　　　　　对吧？

　　　　　　接下来的问题，就是如何计算$len$数组了 ， 这确实是个问题，不过我们可以通过下面的办法解决：

　　　　　　考虑$len[i]$ 以及当前求出的回文右边界$mx$ ， $id$ 是对应的回文中心，如果$i<mx$ 则附上初值$min{mx-i,p[j]}$,其中，$j$是$i$关于$id$的对称坐标，通过中点坐标公式，我们可以得出：$j=id*2-i$ 。

　　　　　　否则($i>=mx$)附上初值$len[i]=1$.

　　　　　　然后，向两边扩展就好了。可以结合下面的图像理解：

　　　　　　

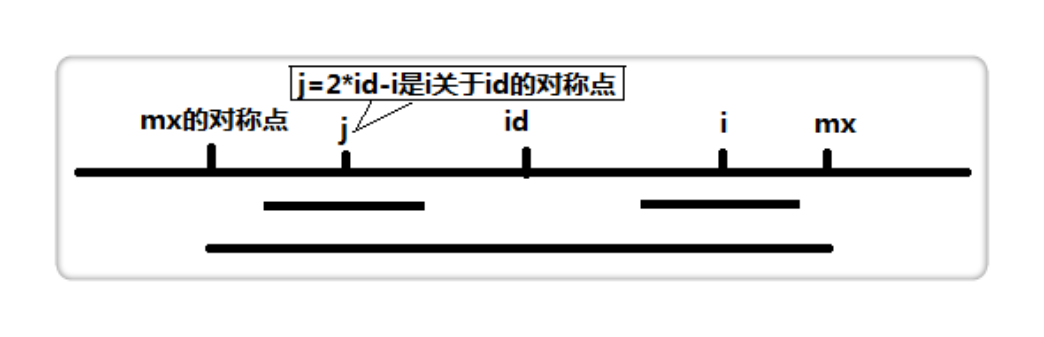
　　　　　　　　　带有下划线的部分，是已经计算得出的回文串。

代码实现:

 void Manache() {
     int pos=,mx=;
     for(register int i=;i<=n;++i) {
         len[i]=i<mx?min(len[(pos<<)-i],mx-i):;
         while(b[i-len[i]]==b[i+len[i]]) len[i]++;
         if(i+len[i]>mx) mx=i+len[i],pos=i;
     }
 }