#C++初学记录（素数判断2）

素数判断2 比较简单的算法，没有技术含量

A prime number is a natural number which has exactly two distinct natural number divisors: 1 and itself. For example, the first four prime numbers are: 2, 3, 5 and 7.

Write a program which reads a list of N integers and prints the number of prime numbers in the list.

Input

The first line contains an integer N, the number of elements in the list.

N numbers are given in the following lines.

Output

Print the number of prime numbers in the given list.

Constraints

1 ≤ N ≤ 10000

2 ≤ an element of the list ≤ 108

Sample Input 1

5

2

3

4

5

6

Sample Output 1

3

Sample Input 2

11

7

8

9

10

11

12

13

14

15

16

17

Sample Output 2

4

对于算法



在素数判断1中，我使用暴力代码判断素数，这无疑是花费时间最长，编写难度最易的代码，在学习的过程中，我发现变成和数学紧密相连，就比如这个素数判断的题目，运用数学方法可以使计算机更快速的跑完程序。

运行的代码

#include<iostream>
#include<math.h>
using namespace std;
int main()
{
	int n;
	cin>>n;
	int b=0,m,count;
	for(int i=0;i<n;i++){
		cin>>m;
		count=1;
        if(m!=2&&m%2==0)
        count=0,break;
	for(int i=2;i<=sqrt(m);i++)
	{
		if(m%2==0)
		{
			count=0;
			break;
		}
		if(m*m%i==0){
		count=0;
		break;}
	}
	if(count==1&&m!=1)
	b++;
    }
    cout<<b;
	return 0; 

}

思考过程



素数是因子为1和本身的数， 如果数m不是素数，则还有其他因子，其中的因子，假如为a,b.其中必有一个大于sqrt(m) ，一个小于 sqrt(m)。也就是说，判断素数只需判断2到sqrt(m)即可，即将判断次数减少一半，来缩短程序运行时间。

素数还有一个特性，就是说除了2以外的所有素数都是偶数。因此，在程序的开始提前将一半偶数排除再外也能缩短大部分的程序运行时间。另外用上面我写的程序中count？=0和break能使条理更加清晰。

错误及调试

刚开始使用sqrt(m)的时候出现了一个错误，就是一组数据的输入Sample Input 2本应输出4，但是程序输出了5



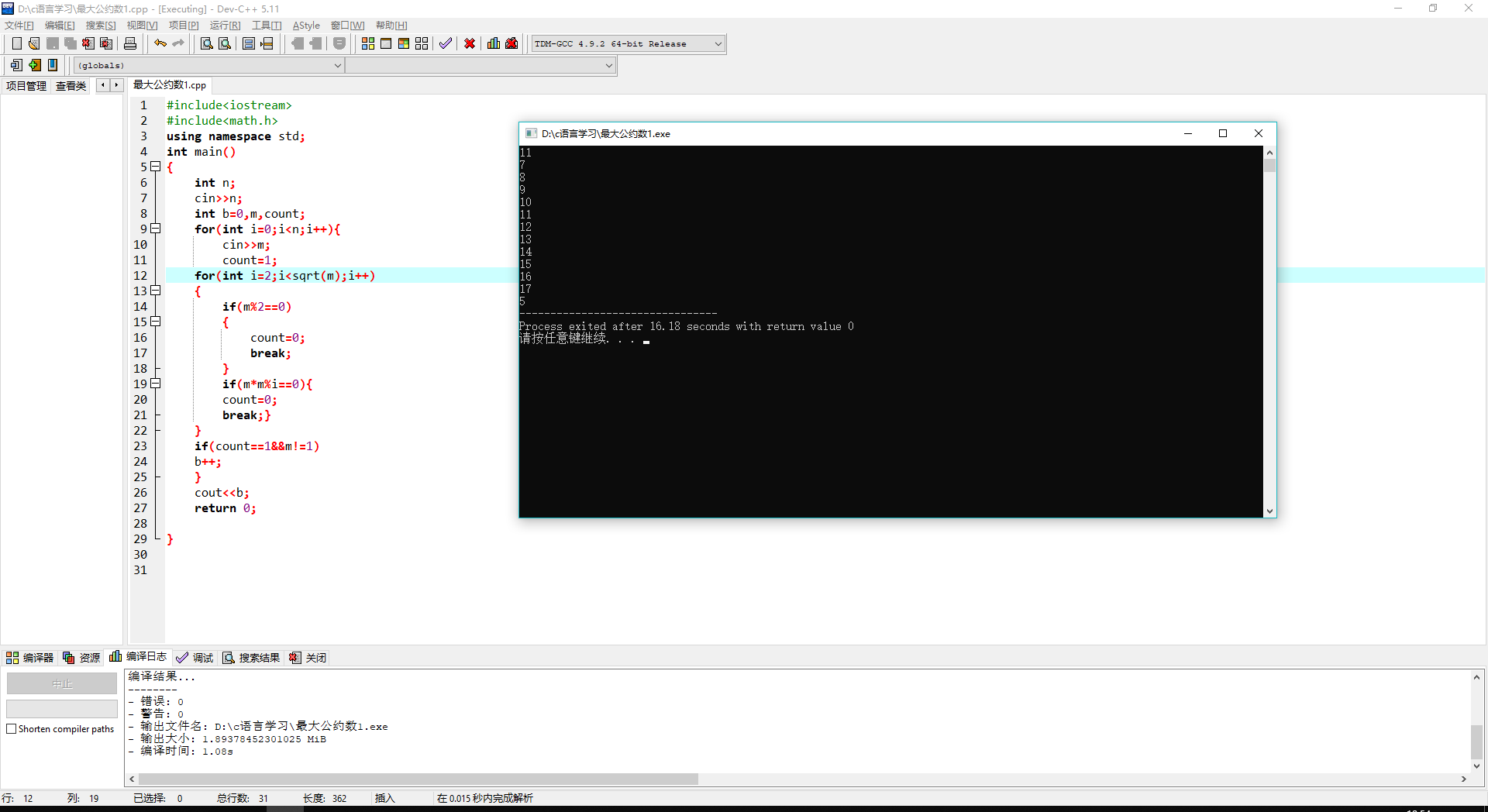
但是经过调试我发现，错误的原因是因为在for循环中，i的终止条件应该是小于等于而不是小于，因为sqrt(m)也能成为一个判定的数据。



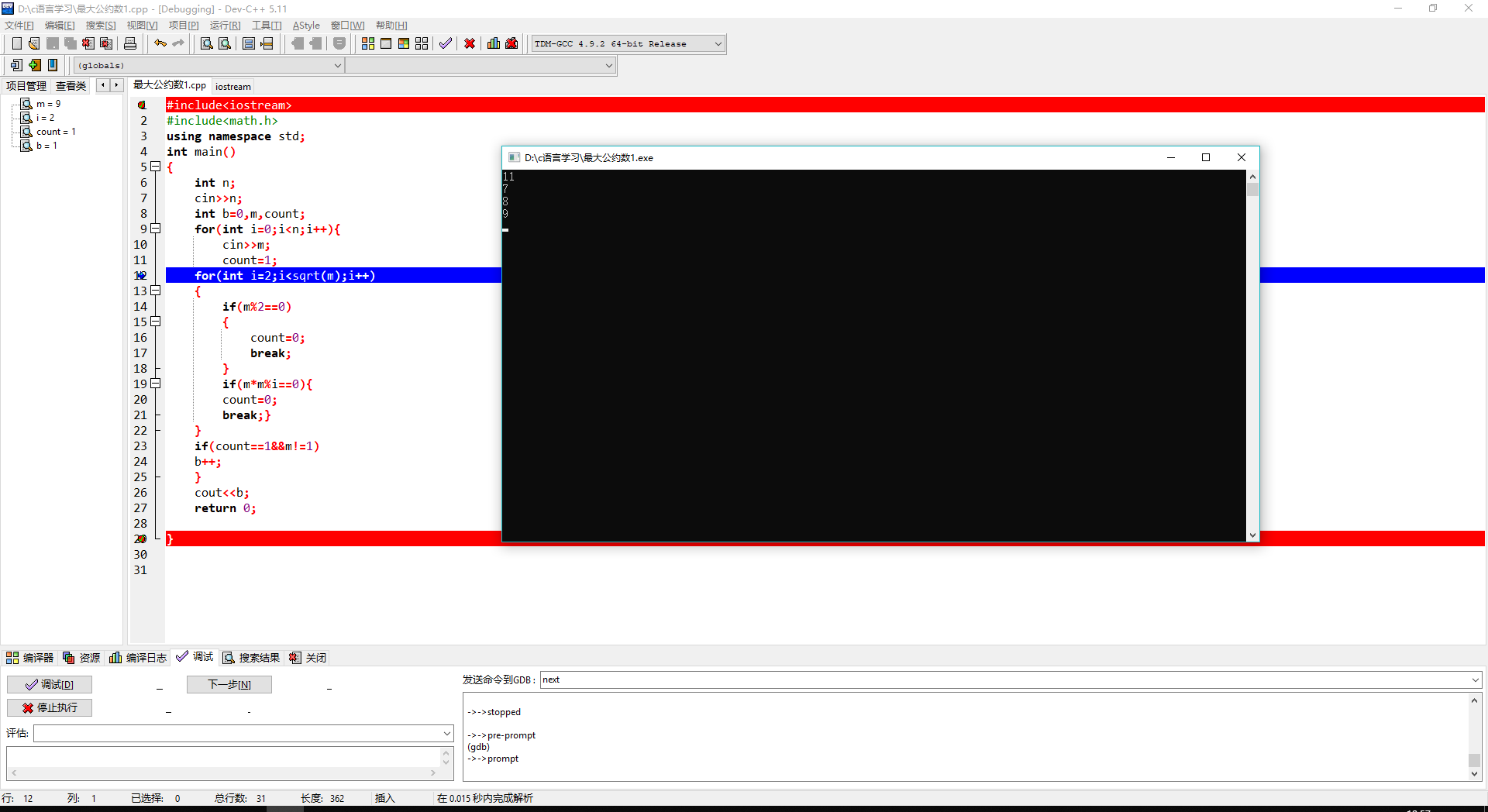
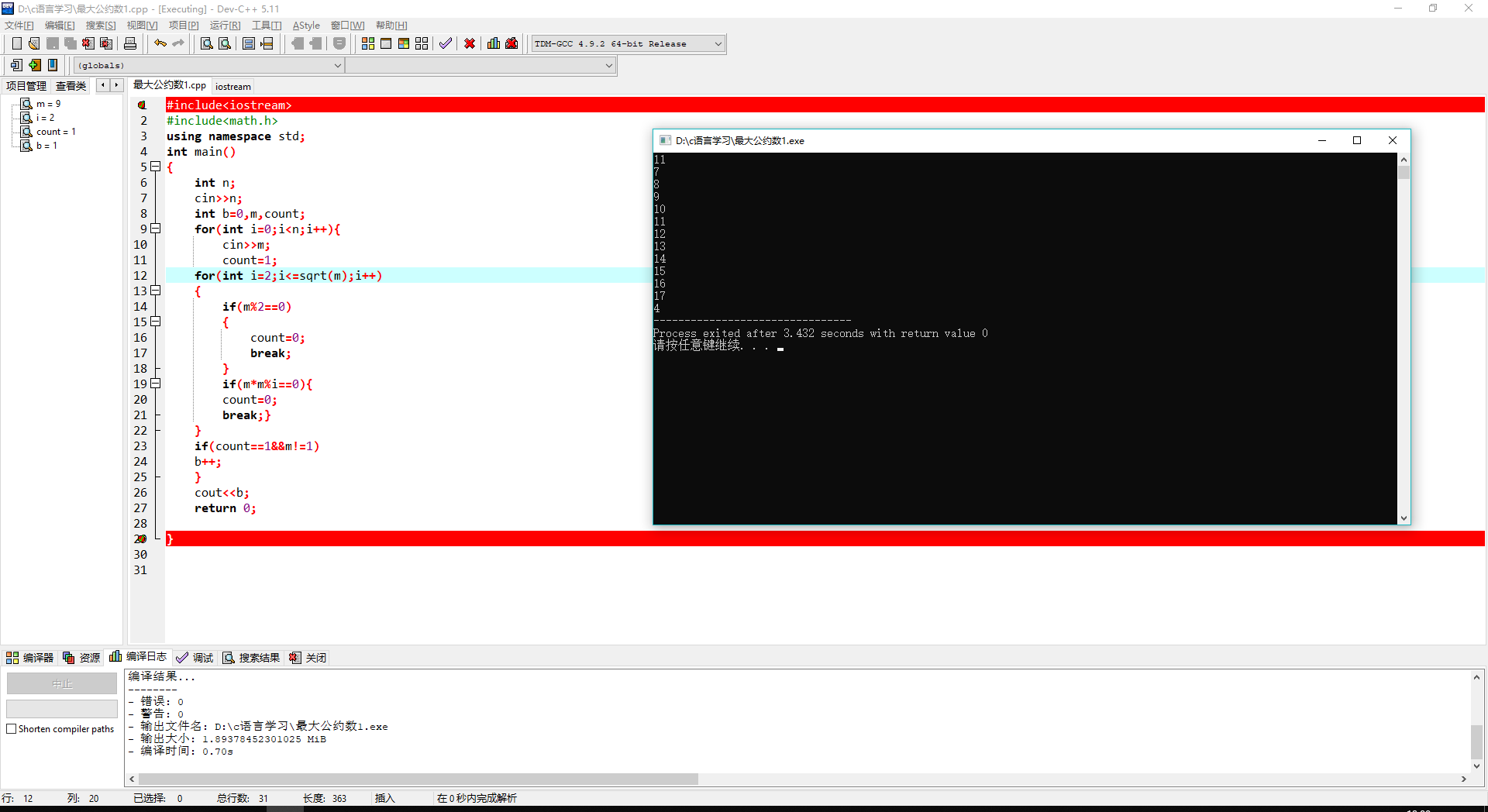
修改后，既是正确的输出程序.