POJ 1418 基本操作和圆 离散弧

Viva Confetti

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 761		Accepted: 319

Description

Do you know confetti? They are small discs of colored paper, and people throw them around during parties or festivals. Since people throw lots of confetti, they may end up stacked one on another, so there may be hidden ones underneath.



A handful of various sized confetti have been dropped on a table. Given their positions and sizes, can you tell us how many of them you can see?



The following figure represents the disc configuration for the first sample input, where the bottom disc is still visible.

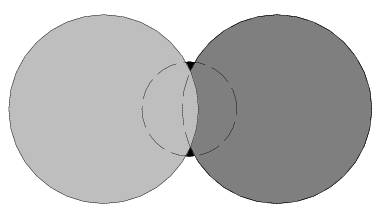
Input

The input is composed of a number of configurations of the following form.



n

x1 y1 r1

x2 y2 r2

...

xn yn rn



The first line in a configuration is the number of discs in the configuration (a positive integer not more than 100), followed by one line descriptions of each disc : coordinates of its center and radius, expressed as real numbers in decimal notation, with
up to 12 digits after the decimal point. The imprecision margin is +/- 5 x 10^(-13). That is, it is guaranteed that variations of less than +/- 5 x 10^(-13) on input values do not change which discs are visible. Coordinates of all points contained in discs
are between -10 and 10.



Confetti are listed in their stacking order, x1 y1 r1 being the bottom one and xn yn rn the top one. You are observing from the top.



The end of the input is marked by a zero on a single line.

Output

For each configuration you should output the number of visible confetti on a single line.

Sample Input

3
0 0 0.5
-0.9 0 1.00000000001
0.9 0 1.00000000001
5
0 1 0.5
1 1 1.00000000001
0 2 1.00000000001
-1 1 1.00000000001
0 -0.00001 1.00000000001
5
0 1 0.5
1 1 1.00000000001
0 2 1.00000000001
-1 1 1.00000000001
0 0 1.00000000001
2
0 0 1.0000001
0 0 1
2
0 0 1
0.00000001 0 1
0

Sample Output

3
5
4
2
2

给定一堆圆，求可见的圆有几个。

问别人的思路；

把圆弧离散化出来。

伏特跳蚤国王(497446970) 12:49:02

然后计算能看见的圆弧

Sd.无心插柳(450978053) 12:49:02

假设一个圆有条圆弧，没有被它之上的圆盖住，那肯定是可见的

Sd.无心插柳(450978053) 12:49:11

但另一种可能

Sd.无心插柳(450978053) 12:49:35

Sd.无心插柳(450978053) 12:50:34

事实上就是某条可见的圆弧盖住的圆

Sd.无心插柳(450978053) 12:50:38

也是可见的

rabbit(1337207267) 12:54:20

是不是一条可见的圆弧仅仅能盖住一个圆。

Sd.无心插柳(450978053) 12:54:55

不是

Sd.无心插柳(450978053) 12:55:11

但可见的肯定是从上往下盖住的第一个圆

代码：

/* ***********************************************
Author :rabbit
Created Time :2014/7/8 13:49:36
File Name :3.cpp
************************************************ */
#pragma comment(linker, "/STACK:102400000,102400000")
#include <stdio.h>
#include <iostream>
#include <algorithm>
#include <sstream>
#include <stdlib.h>
#include <string.h>
#include <limits.h>
#include <string>
#include <time.h>
#include <math.h>
#include <queue>
#include <stack>
#include <set>
#include <map>
using namespace std;
#define INF 0x3f3f3f3f
#define eps 1e-14
#define pi acos(-1.0)
typedef long long ll;
int dcmp(double x){
	if(fabs(x)<eps)return 0;
	return x>0?1:-1;
}
struct Point{
	double x,y;
	Point(double _x=0,double _y=0){
		x=_x;y=_y;
	}
};
Point operator + (Point a,Point b){
	return Point(a.x+b.x,a.y+b.y);
}
Point operator - (Point a,Point b){
	return Point(a.x-b.x,a.y-b.y);
}
Point operator * (Point a,double p){
	return Point(a.x*p,a.y*p);
}
Point operator / (Point a,double p){
	return Point(a.x/p,a.y/p);
}
bool operator < (const Point &a,const Point &b){
	return a.x<b.x||(a.x==b.x&&a.y<b.y);
}
bool operator == (const Point &a,const Point &b){
	return dcmp(a.x-b.x)==0&&dcmp(a.y-b.y)==0;
}
double Dot(Point a,Point b){
	return a.x*b.x+a.y*b.y;
}
double Length(Point a){
	return sqrt(Dot(a,a));
}
double Angle(Point a,Point b){
	return acos(Dot(a,b)/Length(a)/Length(b));
}
double angle(Point a){
	return atan2(a.y,a.x);
}
double Cross(Point a,Point b){
	return a.x*b.y-a.y*b.x;
}
Point vecunit(Point a){
	return a/Length(a);
}
Point Normal(Point a){
	return Point(-a.y,a.x)/Length(a);
}
Point Rotate(Point a,double rad){
	return Point(a.x*cos(rad)-a.y*sin(rad),a.x*sin(rad)+a.y*cos(rad));
}
Point GetLineIntersection(Point p,Point v,Point q,Point w){
	Point u=p-q;
	double t=Cross(w,u)/Cross(v,w);
	return p+v*t;
}
struct Line{
	Point p,v;
	double ang;
	Line(){}
	Line(Point _p,Point _v):p(_p),v(_v){
		ang=atan2(v.y,v.x);
	}
	Point point(double a){
		return p+(v*a);
	}
	bool operator < (const Line &L) const{
		return ang<L.ang;
	}
};
Point GetLineIntersection(Line a,Line b){
	return GetLineIntersection(a.p,a.v,b.p,b.v);
}
struct Circle{
	Point c;
	double r;
	Circle(){}
	Circle(Point _c,double _r):c(_c),r(_r){}
	Point point(double a){
		return Point(c.x+cos(a)*r,c.y+sin(a)*r);
	}
};
Circle C[200];
bool vis[200];
vector<double> pp[200];
int GetCircleCircleIntersection(int s1,int s2){
	Circle c1=C[s1],c2=C[s2];
	double d=Length(c1.c-c2.c);
	if(dcmp(d)==0){
		if(dcmp(c1.r-c2.r)==0)return -1;
		return 0;
	}
	if(dcmp(c1.r+c2.r-d)<0)return 0;
	if(dcmp(fabs(c1.r-c2.r)-d)>0)return 0;
	double a=angle(c2.c-c1.c);
	double da=acos((c1.r*c1.r+d*d-c2.r*c2.r)/(2*c1.r*d));
	Point p1=c1.point(a-da),p2=c1.point(a+da);
	if(p1==p2)return 1;
	pp[s1].push_back(a+da);
	pp[s1].push_back(a-da);
	return 2;
}
bool PointInCircle(Point p, Circle C){
    double dist = Length(p - C.c);
    if(dcmp(dist - C.r) > 0) return 0;
    else return 1;
}
bool CircleInCircle(Circle A, Circle B){
    double cdist = Length(A.c - B.c);
    double rdiff = B.r - A.r;
    if(dcmp(A.r - B.r) <= 0 && dcmp(cdist - rdiff) <= 0) return 1;
    return 0;
}
int main()
{
     //freopen("data.in","r",stdin);
     //freopen("data.out","w",stdout);
     int n;
	 while(~scanf("%d",&n)&&n){
		 memset(vis,0,sizeof(vis));
		 for(int i=0;i<n;i++)pp[i].clear();
		 for(int i=0;i<n;i++)
			 scanf("%lf%lf%lf",&C[i].c.x,&C[i].c.y,&C[i].r);
		 for(int i=0;i<n;i++)
			 for(int j=0;j<n;j++){
				 if(i==j)continue;
				 GetCircleCircleIntersection(i,j);
			 }
		 for(int i=0;i<n;i++){
			 sort(pp[i].begin(),pp[i].end());
			 pp[i].resize(unique(pp[i].begin(),pp[i].end())-pp[i].begin());
		 }
		 for(int i=0;i<n;i++){
			 if(pp[i].size()==0){
				 bool ok=1;
				 for(int j=i+1;j<n;j++)
					 if(CircleInCircle(C[i],C[j])){
						 ok=0;break;
					 }
				 if(ok)vis[i]=1;
			//	 cout<<"han->1"<<endl;
			 }
			 else{
			//	 cout<<"han->2"<<endl;
				 int sz=pp[i].size();
				 pp[i].push_back(pp[i][0]);
				 for(int j=0;j<sz;j++){
					 Point dd=C[i].point((pp[i][j]+pp[i][j+1])/2);
					 bool ok=1;
					 for(int k=i+1;k<n;k++)
						 if(PointInCircle(dd,C[k])){
						//	 cout<<dd.x<<" "<<dd.y<<" "<<k<<endl;
							 ok=0;break;
						 }
					 if(ok){
						 vis[i]=1;
						 for(int k=i-1;k>=0;k--)
							 if(PointInCircle(dd,C[k])){
								 vis[k]=1;break;
							 }
					 }
				 }
			 }
		 }
		 int ans=0;
	//	 cout<<"han  ";for(int i=0;i<n;i++)cout<<vis[i]<<" ";cout<<endl;
		 for(int i=0;i<n;i++)
			 if(vis[i])ans++;
		 cout<<ans<<endl;
	 }
     return 0;
}

版权声明：本文博主原创文章。博客，未经同意不得转载。