矩阵经典题目七：Warcraft III 守望者的烦恼（矩阵加速递推）

https://www.vijos.org/p/1067

非常easy推出递推式f[n] = f[n-1]+f[n-2]+......+f[n-k]。

构造矩阵的方法：构造一个k*k的矩阵。当中右上角的(k-1)*(k-1)的矩阵是单位矩阵，第k行的每一个数分别相应f[n-1]，f[n-2]，，f[n-k]的系数。然后构造一个k*1的矩阵，它的第i行代表f[i]（1 <= i <= k），是经过直接递推得到的。设ans[][]是第一个矩阵的n-k次幂乘上第二个矩阵。f[n]就是ans[k][1]。

注意：用__int64

更为一般的构造递推式矩阵的方法是：

我们能够用上面的方法二分求出不论什么一个线性递推式的第n项。其相应矩阵的构造方法为：在右上角的(n-1)*(n-1)的小矩阵中的主对角线上填1。矩阵第n行填相应的系数，其他地方都填0。

比如。我们能够用以下的矩阵乘法来二分计算f(n)
= 4f(n-1) - 3f(n-2) + 2f(n-4)的第k项：

     

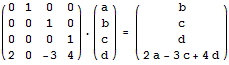
#include <stdio.h>
#include <iostream>
#include <map>
#include <set>
#include <list>
#include <stack>
#include <vector>
#include <math.h>
#include <string.h>
#include <queue>
#include <string>
#include <stdlib.h>
#include <algorithm>
#define LL long long
#define _LL __int64
#define eps 1e-12
#define PI acos(-1.0)
#define C 240
#define S 20
using namespace std;

const int maxn = 15;
const int mod = 7777777;

int k;
struct matrix
{
	_LL mat[maxn][maxn];
	void init()
	{
		memset(mat,0,sizeof(mat));
		for(int i = 1; i <= maxn; i++)
			mat[i][i] = 1;
	}
}a,b;

matrix mul(matrix a, matrix b)
{
	matrix ans;
	memset(ans.mat,0,sizeof(ans.mat));

	for(int i = 1; i <= k; i++)
	{
		for(int g = 1; g <= k; g++)
		{
			if(a.mat[i][g] == 0) continue;
			for(int j = 1; j <= k; j++)
			{
				ans.mat[i][j] = (ans.mat[i][j] + a.mat[i][g] * b.mat[g][j])%mod;
			}
		}
	}
	return ans;
}

matrix pow(matrix a, int n)
{
	matrix ans;
	ans.init();

	while(n)
	{
		if(n&1)
			ans = mul(ans,a);
		a = mul(a,a);
		n >>= 1;
	}
	return ans;
}

int main()
{
	int n;
	while(~scanf("%d %d",&k,&n))
	{
		memset(a.mat,0,sizeof(a.mat));

		for(int i = 1; i <= k-1; i++)
			a.mat[i][i+1] = 1;
		for(int i = 1; i <= k; i++)
			a.mat[k][i] = 1;

		matrix ans = pow(a,n-k);
		memset(b.mat,0,sizeof(b.mat));

		b.mat[0][1] = 1;
		for(int i = 1; i <= k; i++)
		{
			for(int j = 0; j < i; j++)
				b.mat[i][1] += b.mat[j][1];
		}
		ans = mul(ans,b);
		printf("%I64d\n",ans.mat[k][1]);
	}
	return 0;
}