PHP条件运算符的“坑”

今天遇到一个关于PHP 嵌套使用条件运算符(ternary expressions)的问题

现象

先来看一段C语言代码(test.c):

#include<stdio.h>
int main() {
  int x = 1;
  int shit = x == 1 ? 100 :
     x == 2 ? 200 : 300;
  printf("shit的值:%d\n", shit);
  return 0;
}

编译后运行一下

root$ gcc test.c -o test && ./test
shit的值:100

答案在意料之中，因为x==1，所以100被赋值给shit。

但是如果我们用PHP重写一下上文的代码(test.php):

<?php
$x = 1;
$shit = $x == 1 ? 100 :
   $x == 2 ? 200 : 300;
echo "shit的值:$shit\n";

执行一下:

root$ php test.php
shit的值:200

我们发现返回的结果不一样了，这是为什么呢？

排查

首先怀疑可能是PHP中比较运算符(==)和条件运算符(?:)的优先级问题，我们查看一下PHP官方文档

==的优先级比?:更高(C语言也是这样)，所以

$shit = $x == 1 ? 100 :
   $x == 2 ? 200 : 300;

等效于

$shit = ($x == 1) ? 100 :
   ($x == 2) ? 200 : 300;

执行一遍也确实如此，可以排除掉是运算符优先级导致问题的可能性了。

但是官方文档里关于运算符结合方向的举例说明中出现了这么一句话：这跟上文描述的现象很相似，问题应该就在这了。一番查阅之后得到以下结论:

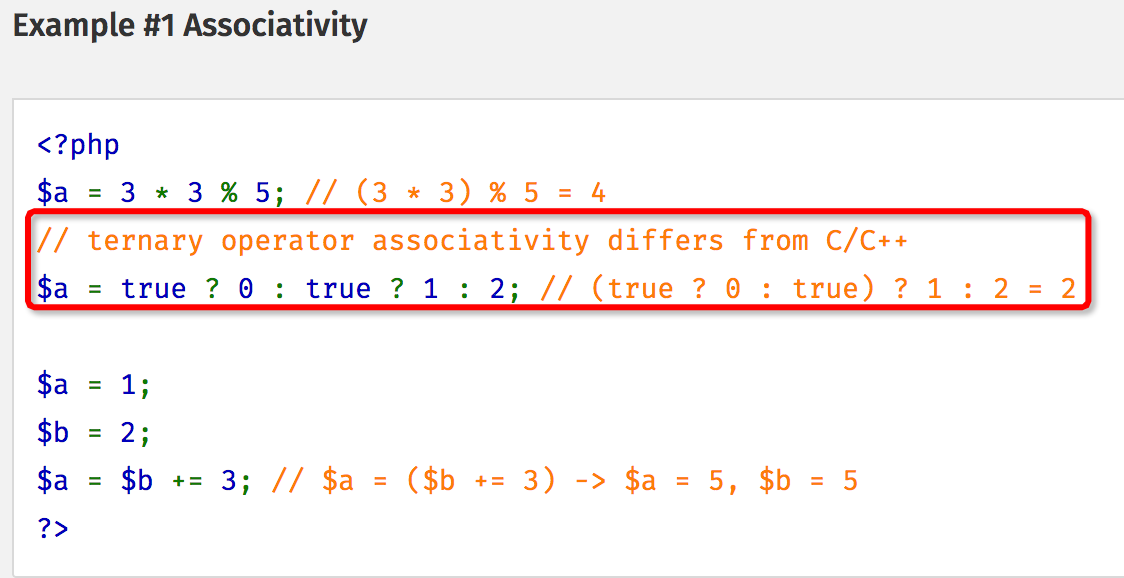
结论

• C语言的条件运算符(?:)的结合方向是从右往左，每次求值都是从最右边的子表达式开始算起，所以

int x = 1;

int shit = x == 1 ? 100 :
     x == 2 ? 200 : 300;
//等效于
int shit = x == 1 ? 100 :
     (x == 2 ? 200 : 300);
//等效于
int shit = x == 1 ? 100 :
     (300);// 100

• PHP的条件运算符(?:)的结合方向是从左往右，每次求值都是从最左边的子表达式开始算起，所以

$x = 1;
$shit = $x == 1 ? 100 :
   $x == 2 ? 200 : 300;
//等效于
$shit = ($x == 1 ? 100 :
   $x == 2) ? 200 : 300;
//等效于
$shit = (100) ? 200 : 300;// 200

介于PHP的条件运算符结合方向，我们无法像C/C++那样 通过嵌套条件运算符来达到if-elseif-elseif-else表达式的效果，除非我们在靠后的子表达式中加上括号，本例中就可以靠这种方式解决:

$shit = $x == 1 ? 100 :
   ($x == 2 ? 200 : 300);

但在条件分支较多的情况下，就会出现代码可读性问题(堆积括号):

$shit = $x == 1 ? 100 :
     ($x == 2 ? 200 :
     ($x== 3 ? 300 :
     ...
     ($x == 8 ? 800 : 900)))))));

由于PHP不堆积括号的写法与C/C++在执行结果上是不一致的，并且只能通过加括号改变默认的结合方向 以达到预期的结果，所以PHP文档里干脆不建议嵌套使用条件运算符:

Note:
It is recommended that you avoid "stacking" ternary expressions. PHP's
behaviour when using more than one ternary operator within a single statement is non-obvious

参考资料

PHP: Ternary Operator - Manual
PHP: Operator Precedence - Manual
php - Ternary operator left associativity - Stack Overflow
Understanding nested PHP ternary operator - Stack Overflow
C 运算符优先级- cppreference.com

原文地址：https://segmentfault.com/a/1190000015634596