VINS-Mono论文笔记（未完）

这是整篇论文的架构，下面针对每一部分进行自己的详细理解。（数学公式的问题没在博客里面解决，都是论文中的截图，尽可能美观==）

一、测量预处理部分（MEASUREMENT PREPROCESSING）

这部分做了两件事情（1）视觉前端处理（2）IMU预积分

（1）首先使用KLT稀疏光流法跟踪图片中的特征点，检测器通过设置两个相邻特征之间的像素的最小分离来执行均匀的特征分布，每张图片的特征点数目在100-300。检测出来的2D特征点经过F矩阵的RANSAC去除外点，然后投影到一个单位球面。

　　同时，该阶段选择关键帧，关键帧的选择有2个条件。①平均视差。②特征点的数量。注意：平均视差是由平移和旋转引起的，但是纯旋转是没有办法进行三角化的，为了弥补这一部分采用IMU短期预积分；另外特征点数量低于阈值的时候，可能会完全丢失特征点，故选出来做关键帧。

（2）IMU预积分是这部分的重点。

原始IMU的测量值为：

假设噪声服从高斯分布：

由于加速度偏差和陀螺仪的偏差为随机游走建模，所以他们的导数也服从高斯分布。即：

我们的估计器是需要估计位置p，速度v和旋转q的，它们满足下面的迭代式：

从式子（3）中可以看出来，当前时刻的状态可以通过上一时刻状态来迭代求得，这个式子包含积分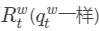，表示t时刻世界坐标系下的旋转，是一个需要估计的量。这个估计的量是需要不断地更新变化，如果按照式子（3）进行计算，那么每次进行变化都需要重新积分，这很消耗计算资源。故在（3）中左右同时乘以一个旋转矩阵Rw->bk，这样就把坐标系转换到了bk下，当状态量变化的时候，可以通过矩阵乘法把相对变化量变成绝对变化量。（可以这么理解：绝对变化量是不变的，相对变化量是变化的。所以这样做是为了较少计算负担）当然这样做的目的如下：

1. 相对k帧的IMU进行积分，不会有累积误差；

2. 即使后面调整了位姿，相对位置不变；

3. 这个旋转矩阵为单位矩阵E，后面每出现一个IMU数据，都可以用任何一种数值积分的方法计算；同时可以将重力加速度提取到积分号外面不参加积分，相当于在重力参考系中积分，计算量也会减少。

于是，得到(5)式：

离散时间的计算：

论文中使用的是Euler积分方式，代码中使用的是中值积分。

当变化量是较小的时候，可以使用一阶近似求得α，β和γ；如果变化比较大，再重新计算。

对于离散时间的估计量的计算式（7）：（假设噪声项为0）

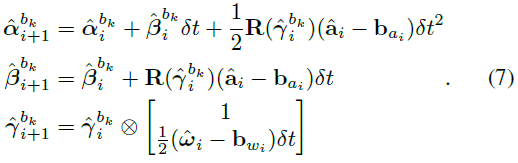
得到当前需要优化的变量的雅可比矩阵J和协方差矩阵P，最后得到从k到k+1的测量量，用当前的状态两计算出来的就是估计，相减就是残差。观测方程：

IMU积分后，会全部给后端ceres做优化。