poj2595（凸包）

Min-Max

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 2192		Accepted: 502

Description

Define the following function




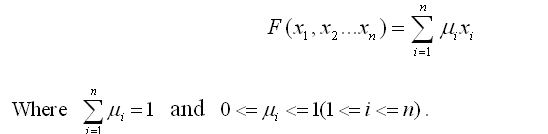
Given the value C of F(p1, p2 ... pn), can you find the minimum and maximum value of F(q1, q2 ... qn)?

Input

The input contains several test cases. For each test case, it contains three lines.



Line 1: two integers n (1<= n <= 50000) and C.

Line 2: n integers p1, p2 ... pn (|pi| < 1000 for 1 <= i <= n).

Line 3: n integers q1, q2 ... qn (|qi| < 1000 for 1 <= i <= n).

Output

For each test case, output the minimum and maximum value in a single line with the fraction rounded to 3 decimal places.

Sample Input

2 1
3 1
0 2

Sample Output

2.000 2.000

Source

POJ Monthly--2005.08.28,Static

题目一看就很熟悉很熟悉很熟悉啊！

我怎么一眼看到就想起詹森不等式呢。

。。。

事实上是重心公式。C是重心的x,而y在凸包上。

所以问题就变成求凸包啦！

求完凸包就要绕着凸包上每一条边求极值并更新。

/***********************************************************
	> OS     : Linux 3.13.0-24-generic (Mint-17)
	> Author : yaolong
	> Mail   : dengyaolong@yeah.net
	> Time   : 2014年10月14日 星期二 07时44分53秒
 **********************************************************/
#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
const double INF = 1e50;
const int N = 61111;
struct Point
{
    int x, y;
} ;
Point p[N], stk[N];
Point minp;
int top;
double cross ( Point &o,  Point &a,  Point &b )
{
    return ( a.x - o.x ) * ( b.y - o.y ) - ( a.y - o.y ) * ( b.x - o.x );
}
double dist ( Point &A,  Point & B )
{
    return hypot ( A.x - B.x, A.y - B.y );
}
bool cmp ( Point A, Point B )
{
    double k = cross ( minp, A, B );
    if ( k < 0 ) return 0;
    if ( k > 0 ) return 1;
    return dist ( minp, A ) < dist ( minp, B );
}
void Gramham ( int n )
{
    int i;
    for ( i = 1; i < n; i++ )
    {
        if ( p[i].y < p[0].y || ( p[i].y == p[0].y && p[i].x < p[0].x ) )
        {
            swap ( p[i], p[0] );
        }
    }
    minp = p[0];
    p[n] = p[0];
    sort ( p + 1, p + n, cmp );
    stk[0] = p[0];
    stk[1] = p[1];
    top = 1;
    for ( i = 2; i < n; i++ )
    {
        while ( top >= 1 && cross ( stk[top - 1], stk[top ], p[i] ) <= 0 ) --top;
        stk[++top] = p[i];
    }
}
double mmin, mmax;
int c;
void update ( Point a, Point b )
{
    if ( a.x > b.x )
    {
        swap ( a, b );
    }
    if ( a.x <= c && b.x >= c )
    {
        if ( a.x == c && b.x == c )
        {
            mmax = max ( mmax, ( double ) max ( a.y, b.y ) );
            mmin = min ( mmin, ( double ) min ( a.y, b.y ) );
        }
        else
        {
            double k = ( ( double ) c - a.x ) / ( ( double ) b.x - a.x ) * ( b.y - a.y ) + a.y;
            mmax = max ( mmax, k );
            mmin = min ( mmin, k );
        }
    }
}
int main()
{
    int n,  i;
    while ( ~scanf ( "%d%d", &n, &c ) )
    {
        for ( i = 0; i < n; i++ )
        {
            scanf ( "%d", &p[i].x );
        }
        for ( i = 0; i < n; i++ )
        {
            scanf ( "%d", &p[i].y );
        }
        if ( n == 1 )
        {
            printf ( "%.3f %.3f\n", ( double ) p[0].y, ( double ) p[0].y );
            continue;
        }
        Gramham ( n );
        stk[++top] = stk[0];
        mmin = INF, mmax = -INF;
        for ( i = 1; i <= top; i++ )
        {
            update ( stk[i - 1], stk[i] );
        }
        printf ( "%.3f %.3f\n", mmin, mmax );
    }
    return 0;
}