谈一谈Dijkstra

dijkstra呢是最短路三大算法之一。很多人都觉得不如spfa，但是这两者在跑稠密图时，dijkstra有奇效

在讲之前先说一说食用方法：

适用于有向的无负权值的图。

样例飘过

6 9 1      //n个点，m条边，以s为起点
1 3 3
1 6 10
3 6 5
4 3 7
1 4 4
4 2 5
5 2 4
4 5 6
3 5 6

　　

0 9 3 4 9 8

　　

上面这组样例我们让他更直观一些

神图警报，请开启护眼模式

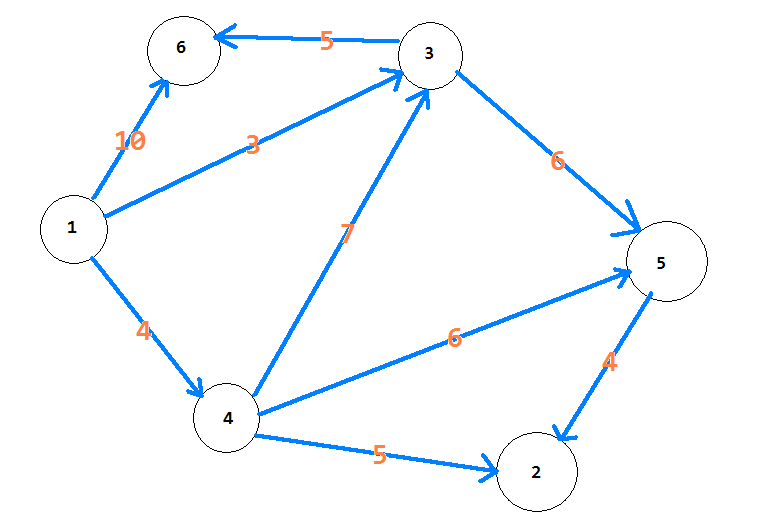
真心累

首先我们应该知道dijkstra的核心思想是贪心。

定义一个$dis$数组，$dis[i]$表示从起点到i节点的距离，我们在程序一开始的时候把dis全部赋值成INF，

只把dis[s]赋值成0,(因为s->s == 0),这时候我们需要定义一个bool行的数组book,book[i]表示节点是否被访问过。

那么接下来就进入核心部分了。

我们每次从所有的节点中找一个dis值最小的，当让我们知道第一次肯定会找到s，然后以这个点为节点向外扩展，如果在已知的边的基础上可以找到更短的到某一个点的路径，那么就将这个路径更新。

这么说可能有点抽象，那么让我们看点实在的

上图

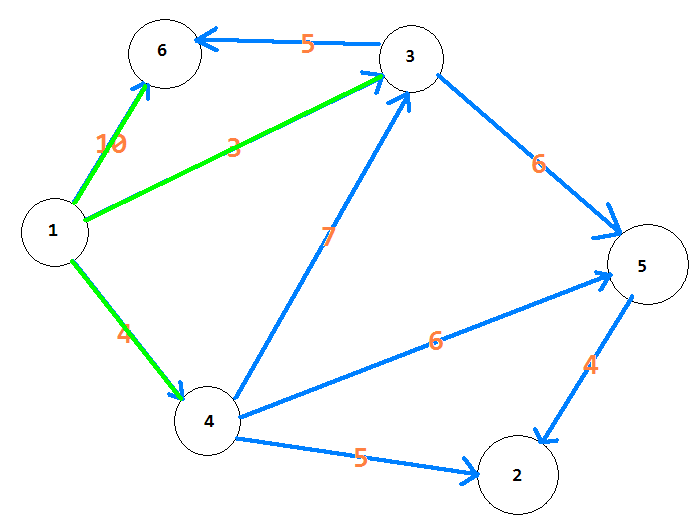
第一次找到了dis值最小的1号节点向外扩展，那么现在dis数组的值为

$dis[1] = 0, dis[2] = INF, dis[3] = 3, dis[4] = 4, dis[5] = INF, dis[6] = 10$

记得要把book[1]变成1，代表已经访问过。

接下来进行第二次扩展，这时候由于dis[1]我们已经访问过，所以接下来就会选择3号节点进行扩展

如图

从3号节点出去的边可以连到5和6，连5时毫无疑问会更新，但是再连6时，我们发现dis[6]已经扩展了一次，那么怎么办呢，很明显，从1走到3再走到6的话总路程为dis[3]加上3到6的路程，共为8，比现有的dis[6]要小，所以我们就要再更新dis[6] = 8;

通过这么一次次的更新，我们就能把这张图的最短路跑完，注意是单源最短路。

说了这么多我们来看下代码，但是我这个代码有个很玄学的地方，就是建边的时候我写的是用数组实现的邻接链表，但是原理是和结构体实现的邻接链表相同，大家将就着看，如果看不懂那就参考一下下面这篇文章

【坐在马桶上看算法】算法8：巧妙的邻接表（数组实现）

这里讲的非常的详细，我当初就是看的这里。

---

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#define MAXN 500008
#define INF  2147483647
#define maxn 10008

using namespace std;

int n, m, s;
int next[MAXN], first[MAXN];
int u[MAXN], v[MAXN], w[MAXN];
int dis[maxn];
bool book[MAXN];

int main() {
	scanf("%d%d%d", &n, &m, &s);
	for(int i=1; i<=n; i++) {
		dis[i] = INF;
	}
	dis[s] = 0;
	memset(first, -1, sizeof(first));
	for(int i=1; i<=m; i++) {
		scanf("%d%d%d", &u[i], &v[i], &w[i]);
		next[i] = first[u[i]];
		first[u[i]] = i;
	}
	for(int i=1; i<n; i++) {
		int minn = INF, x;
		for(int j=1; j<=n; j++) {
			if(dis[j] < minn&&book[j] == 0) {
				minn = dis[j];
				x = j;
			}
		}
		book[x] = 1;
		int k = first[x];
		while(k != -1) {
			if(dis[v[k]] > dis[u[k]]+w[k]) {
				dis[v[k]] = dis[u[k]]+w[k];
			}
			k = next[k];
		}
	}
	for(int i=1; i<=n; i++) {
		printf("%d ", dis[i]);
	}
}