【LeetCode】3 、Longest Substring Without Repeating Characters

题目等级：Medium

题目描述：

  Given a string, find the length of the longest substring without repeating characters.

  Example 1:

Input: "abcabcbb"
Output: 3
Explanation: The answer is "abc", with the length of 3.

  Example 2:

Input: "bbbbb"
Output: 1
Explanation: The answer is "b", with the length of 1.

  Example 3:

Input: "pwwkew"
Output: 3
Explanation: The answer is "wke", with the length of 3.
             Note that the answer must be a substring, "pwke" is a subsequence and not a substring.

  题意：给定一个字符串，找到其中不含重复字符的最长子串的长度，要注意子串和子序列的区别。

---

解题思路：

  一般对于这种稍微复杂一些的题目，首先可以想到的是最基础的暴力解法，然后我们可以在暴力解法的基础上思考相应的改进和提升效率的算法，针对本题我们给出以下三种解法。

  解法一：Brute Force暴力解法

  暴力解法自然是最直观的，既然是求不含重复字符的最长子串，我们可以通过穷举所有的子串，判断其中是否含有重复字符，并记录最大长度。假设我们现在有一个函数能判断一个字符串中是否包含重复字符，然后只需要一个两层循环枚举所有的子串，即可得到结果。

  那么这个判断一个字符串是否包含重复字符的函数该怎么实现呢，首先要判断一个字符串是否包含重复字符，总得每一个字符都比较过才能知道重复与否，因此大致这个算法应该是O(n)复杂度。再进一步思考，要判断是否重复，集合不正好是不包含重复元素的数据结构吗，因此，只需用一个set保存之前的元素，我们就可以知道是否重复了。

  对于这个暴力解法，首先要穷举所有的子串需要两层循环，每个子串判断重复与否还需要一层循环，因此，整体时间复杂度是O(n^3)，由于使用了一个Set，空间复杂度为O(n)。

  然而，我们把以下的代码实现在LeetCode上提交，会发现提示Time Limit Exceeded，因为超时无法通过。

class Solution {
    public int lengthOfLongestSubstring(String s) {
        if(s==null || s.length()==0)
            return 0;
        int len=s.length();
        int res=1;
        for(int i=0;i<len;i++){
            for(int j=i+1;j<len;j++){
                if(allUnique(s,i,j))
                    res=Math.max(res,j-i+1);
            }
        }
        return res;
    }

    public boolean allUnique(String s,int i,int j){
        Set<Character> set=new HashSet<>();
        for(;i<=j;i++){
            char c=s.charAt(i);
            if(set.contains(c))
                return false;
            set.add(c);
        }
        return true;
    }
}

  解法二：滑动窗口解法

  暴力法由于超时无法通过，因此我们必须改进算法，提升时间效率。回过头来，我们再看暴力解法，可以发现实际上这个解法做了很多重复的和不必要的工作，主要体现在以下两个方面：

  （1）分别判断每一个子串是否重复，这里面是有很多重复的工作的，实际上子串和子串之间不是孤立的，是有联系的。比如，如果我们已经判断了字符串str中从i到j（i和j是下标）是不包含重复字符的，那么在判断从i到j+1时，完全没必要从头在来判断这个子串，因为我们只需要知道第j+1个字符是否在从i到j中出现过就可以了。

  （2）如果我们已经判断了字符串str中从i到j（i和j是下标）是包含重复字符的，那么以第i个字符开始，以第j个字符之后的所有字符结尾的字符串都没必要再判断了，因为它一定也是包含重复字符的。此时直接增大i的值就可以了。

  综合以上两点，实际上我们不难得出，这实际上就是一个滑动窗口从前向后移动的过程，如下图所示：

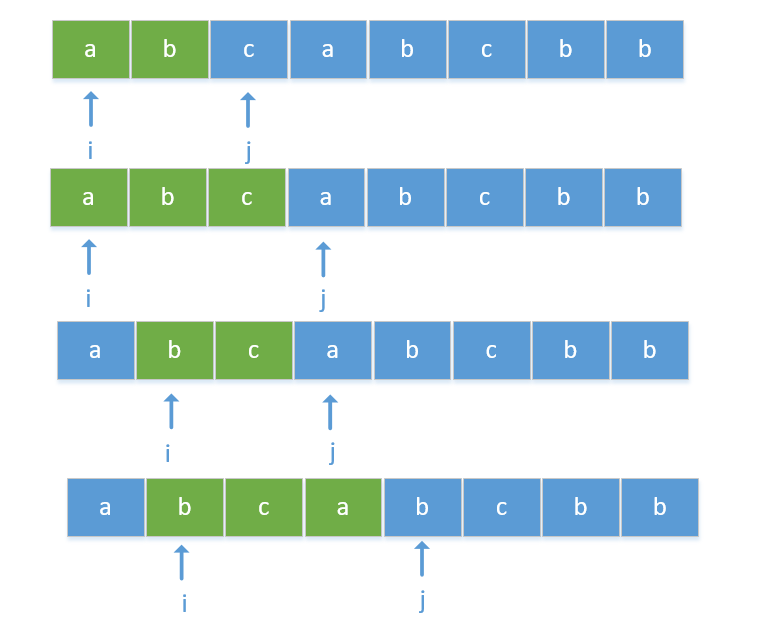
  由此，我们可以得到如下所示的代码实现，即滑动窗口解法。其中只有一层循环，并且最坏的情况下循环次数为2n次（即j先加到最大，然后i由逐步加大，各需要n次），所以，时间复杂度为O(2n)，仍然用了一个set保存字符，所以空间复杂度为O(n)。

class Solution {
    public int lengthOfLongestSubstring(String s) {
        if(s==null || s.length()==0)
            return 0;
        int len=s.length();
        int i=0,j=0;
        Set<Character> set=new HashSet<>();
        int res=0;
        while(i<len&&j<len){
            char c=s.charAt(j);
            if(set.contains(c)){ //注意这里，并不只是i+1，对应的字符也要从集合中删掉
                set.remove(s.charAt(i));
                i++;
            }else{
                set.add(c);
                res=Math.max(res,j-i+1);
                j++;
            }
        }
        return res;
    }
}

  解法三：改进的滑动窗口

  解法二实际上已经将复杂度降到了O(n)级别，正如我们前面所说，要判断每个字符是否重复，最起码每个字符都要比较到，否则不可能知道重复与否，因此直观上我们应该有一个大概的认识：此题的算法很有可能应该是不会比O(n)更优了，当然这只是一个粗略的想法。

  解法三实际上也就是针对解法二的一个地方进行了优化。考虑如下情况：

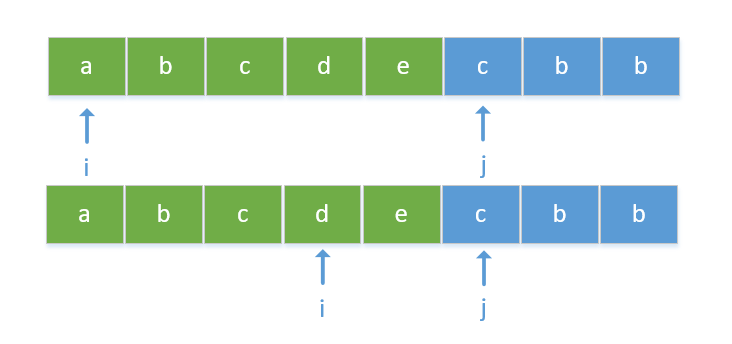
  此时，j指向c，根据滑动窗口解法，前面的窗口中存在c，因此重复，此时应该i增大1，指向b，但是很明显，从b到j中还是包含重复的c，因此一定是仍然重复的，所以当遇到重复时，i没必要只加一，可以一步到位，直接定位到重复字符的下一个去，比如这里，可以直接指向d，因为前面无论哪个都包含c，都会重复。

  因此，我们就可以得到对应的解法三，这里由于需要保存字符，还需要保存位置，因此必须将set改为Map<字符，下标>。这样，我们看到，实际上i是跳跃向前的，因此最坏情况下也只需要n次循环，时间复杂度由O(2n)降到了O(n)，空间复杂度只是由set换为map，仍为O(n)。

  代码如下：

class Solution {
    public int lengthOfLongestSubstring(String s) {
        if(s==null||s.length()==0)
            return 0;
        int len=s.length();
        int i=0,j=0,res=0;
        Map<Character,Integer> map=new HashMap<>();
        while(j<len){
            char c=s.charAt(j);
            if(map.containsKey(c)){
                i=Math.max(i,map.get(c)+1);
            }
            res=Math.max(res,j-i+1);
            map.put(c,j);
            j++;
        }
        return res;
    }
}

  除此之外，正如很多题中用到的，如果针对于一些特殊的字符集，比如ASCLL码，就可以用字符数组代替哈希表，字符的ASCII码作为下标，数组值为字符的位置。

总结

  对于本题，这三种解法实际上正是LeetCode的题解中给出的，从暴力到比较巧妙的滑动窗口，再到对其进行改进，跳跃向前，时间复杂度逐步降低，这里，我认为重点不是如何解决这一道题，而是如何分析，从哪里能给改进，一步一步寻找最佳解法。