2016 ACM-ICPC CHINA-Final

补题进度：10/12

地址：http://codeforces.com/gym/101194

A(签到)

略

B(数位DP)

题意：

　　定义一个01字符串为good串当且仅当将其奇数位或者偶数位单独拎出来是个回文串。

　　输出长度为n(<=1e5)的字典序排在第k(<=1e18)位的good串

分析：

　　很明显的数位dp，从高位到低位确定，尝试放0/1，看看以该前缀为前缀的good串个数，与当前的k相比较就可以知道到底填0还是1

　　那么我们只需要解决一个子问题就行了，即已知确定的前缀，问有多少个长度为n的以该前缀为前缀的good串

　　方案数=奇位上是回文串+偶位上是回文串-奇偶位都是回文串

　　单独考虑奇数位、偶数位，那么很明显mid之前的位置都是自由位，而mid之后的位置要根据前面的来

　　有很多很多的细节要注意

C(set维护区间)

题意：

　　给出长度为n(n<=1000)的数组，你需要找出两个区间[a,b][c,d]，其中a<=b<c<=d，使得a~b的所有数和c~d的所有数数字都没重复，求b-a+d-c+2的最大值

分析：

　　考虑枚举右边区间的左端点l，r不断向右边滑动，动态维护左边的情况

　　我们可以事先将1~l-1的所有极大区间都放入一个set<pair<int,int> >中保存

　　然后随着r的滑动，我们把color[r]对应的颜色的所有位置x删除，即如果set中有一个区间满足first<=x<=second，那么就把这个区间删除

　　当然删除后别忘了还要建立两个新区间：[minl,x-1]和[x+1,maxr]

　　分析复杂度：枚举l需要O(n)，r滑动需要O(n)，初始区间数是O(n)，每个区间只会被删除一次，即只会被遍历一次（根据first和second的单调性），而每次只会加进来O(1)个区间，所以总共复杂度是O(n^2logn)的

D(二分答案)

题意：

　　给出n(<=3e5)个数字，你需要挑出其中若干个组成若干组，每组K(k<=64)个数字，将每组中的数字排序，不妨设A[0] A[1] A[2] .. A[k] ，要满足A[0]*2<=A[1],A[1]*2<=A[2],....，问最多能分成多少个组？

分析：

　　考虑二分答案组数mid，那么就去判定能否组成这mid组

　　从所有数字中挑选出mid个作为mid组的每组的第一个数字，然后再从剩余的数字按顺序中挑选出满足条件的最小的作为每组的第二个数字……，看能否每组取满k个就行了

　　具体做的时候容易想到用set来维护，这样在onsite的话是过不了的，因为有100组数据（但cf上跑过去了），其实弄个指针往后扫就可以完成O(n)的判定了，这样就ok了

　　时间复杂度O(nlogn)

E(高精度)

题意：

　　略

分析：

　　按照题意自然列出要求最优的式子，很明显就能贪心，但这题问题是卡了精度（据说onsite时的非常毒瘤的题），于是rbb就用java写过了

　　后来rbb把我的c++代码改了改也过了，具体就是把输入的数字全部乘上了1000变成了整数，好玄学啊？rbb吼强惹？

F(后缀数组)

题意：

　　给出一些字符串，在第一个字符串中求出一个最短的子串，使得这个子串在后面的所有字符串中都没出现过

分析：

　　很显然的后缀数组，先将所有字符串用$连接，再基本操作搞出sa[] rk[] height[]

　　我们按照sa[]中的顺序从前往后考察每个后缀，分成两类，A类表示sa[i]<=strlen(s[1])-1，B类表示sa[i]>strlen(s[1])-1

　　对于每个A类字符串，我们求出它和所有B类字符串的lcp，取个最大值maxlcp，看看加上这个maxlcp后是否越过了strlen(s[1])-1即可知道是否贡献可能答案

　　进一步思考，因为越远处的B类串和该A类串的lcp越小，所以只需要对每个A类串找其两边的最靠近它的B类串就行了，这只需要一个O(n)的预处理就行了

　　时间复杂度O(nlogn)

G(套路+线段树合并)

题意：

　　给出一个n(n<=2e5)个点，m(m<=2e5)条边的无向图，有边权(边权<=1e6)，每个点有自己的颜色(<=1e5)

　　有q(q<=2e5)个询问，每次询问一个(start,limit)，表示从start点出发，只能走边权<=limit的边，走出一个以start为中心的连通块，问这个连通块里出现次数最多的点的颜色是什么颜色（出现次数相同输出颜色编号最小的），强制在线

分析：

　　强制在线，毫无思路，翻了翻qls的wiki题解，get到了新套路

　　处理这类有关限制边权的连通问题，仍旧先做kruskal跑最小生成树，但若要将两个子树u和v合并，那么我们新建一个点k，k->u,k->v，边权就是当前边的边权，这样建一个新的树

　　这样对于每个询问(start,limit)，就是从start一直向上跳，直到当前树边的边权>limit，得到了最远的父亲节点f

　　那么该询问的答案其实就是以f为根的子树的叶子节点的众数

　　线段树合并即可

　　最后向上跳的时候树上倍增就行了，但数据比较弱，我暴力跳在cf上5000ms过了

　　时间复杂度O(nlog^2n)

H(数学推导)

题意：

　　在一个n行m列的棋盘上，给每个格子填上权值在[1,K]里的整数(n,m,k<=200)。

　　若某个位置(i,j)满足该位置的数字是该行该列的所有数中严格最大的，那么该位置就是good位置

　　令$A_g$表示该棋盘恰好有g个good位置的方案数，要求

　　

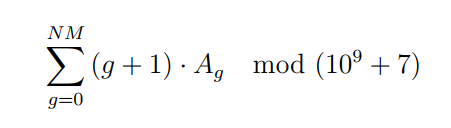
分析：

　　正面去思考如何求$A_g$是很麻烦的事情，不过好像可以用dp+容斥解决

　　我们去单独考虑一个位置(i,j)作为good位置的情况，也就是说枚举该位置的数字，就知道了同行同列的元素填数的方案数，外面的元素随便填

　　如果我们把这些东西累加，其实就是Σ$gA_g$，因为考虑一种情况，假设(i,j)恰好是g=i时候的一个组成部分，那么去算该状态下的另外i-1个位置，都会把(i,j)再算一遍，也就是算了i遍

　　于是我们就知道了Σ$gA_g$如何球了，剩下的Σ$A_g$就是对所有方案数的求和了

　　时间复杂度O(KlogK)

J(费用流)

题意：

分析：

　　对格子黑白染色，黑色格子出横边，白色格子出竖边，将每个格子拆成两个点L[i]、R[i]形成二分图

　　对于题目的要求，形成循环流，即相当于每个点都要找到它的后继，然后它后继再找后继.....一直回到自身，类似置换群；对于那些不强制要求占领的格子，可以L[i]->R[i]表示自己匹配自己

　　于是建图如下：

　　　　对于合法的边权(u,v,w)，L[u]->R[v]，边权为w；对于不强制要求占领的格子i，L[i]->R[i]，边权为0,

　　然后对于该图求最大权匹配就行了，可以用费用流做

L(签到)

略