FM算法及FFM算法

转自：http://tech.meituan.com/deep-understanding-of-ffm-principles-and-practices.html

http://blog.csdn.net/google19890102/article/details/45532745

FM原理 =>解决稀疏数据下的特征组合问题，

1) 可用于高度稀疏数据场景；2) 具有线性的计算复杂度

对于categorical(类别)类型特征，需要经过One-Hot Encoding转换成数值型特征。CTR/CVR预测时，用户的性别、职业、教育水平、品类偏好，商品的品类等，经过One-Hot编码转换后都会导致样本数据的稀疏性。特别是商品品类这种类型的特征，如商品的末级品类约有550个，采用One-Hot编码生成550个数值特征，但每个样本的这550个特征，有且仅有一个是有效的（非零）。由此可见，经过One-Hot编码之后，大部分样本数据特征是比较稀疏的(即特定样本的特征向量很多维度为0)，同时导致特征空间大。(对于每一个特征，如果它有m个可能值，那么经过独热编码后，就变成了m个二元特征(取值0或1)。并且，这些特征互斥，每次只有一个激活。因此，数据会变成稀疏的.) sklearn中preprocessing.OneHotEncoder实现该编码方法。

通过观察大量的样本数据可以发现，某些特征经过关联之后，与label之间的相关性就会提高。例如，“USA”与“Thanksgiving”、“China”与“Chinese New Year”这样的关联特征，对用户的点击有着正向的影响。换句话说，来自“China”的用户很可能会在“Chinese New Year”有大量的浏览、购买行为，而在“Thanksgiving”却不会有特别的消费行为。这种关联特征与label的正向相关性在实际问题中是普遍存在的，如“化妆品”类商品与“女”性，“球类运动配件”的商品与“男”性，“电影票”的商品与“电影”品类偏好等。因此，引入两个特征的组合是非常有意义的。(我的理解：个性化特征)

一般的线性模型为：

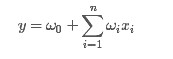
从上面的式子很容易看出，一般的线性模型压根没有考虑特征间的关联(组合)。为了表述特征间的相关性，我们采用多项式模型。在多项式模型中，特征x_i与x_j的组合用x_ix_j表示。为了简单起见，我们讨论二阶多项式模型。具体的模型表达式如下：

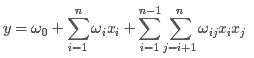
上式中，n表示样本的特征数量,x_i表示第i个特征。 
与线性模型相比，FM(Factorization Machine)的模型就多了后面特征组合的部分。

从公式(1)可以看出，组合特征的参数一共有 n(n−1)/2 个，任意两个参数都是独立的。然而，在数据稀疏性普遍存在的实际应用场景中，二次项参数的训练是很困难的。其原因是，每个参数 w_ij 的训练需要大量 x_i 和x_j都非零的样本；由于样本数据本来就比较稀疏，满足“x_i 和 x_j 都非零”的样本将会非常少。训练样本的不足，很容易导致参数 w_ij 不准确，最终将严重影响模型的性能。

如何解决二次项参数的训练问题呢？矩阵分解提供了一种解决思路。在model-based的协同过滤中，一个rating矩阵可以分解为user矩阵和item矩阵，每个user和item都可以采用一个隐向量表示。我们把每个user表示成一个二维向量，同时把每个item表示成一个二维向量，两个向量的点积就是矩阵中user对item的打分。

类似地，所有二次项参数W _i,j可以组成一个对称阵W,那么这个矩阵就可以分解为 W=VV^T,V的第i行便是第i维特征的隐向量。换句话说，每个参数W _i,j = <V _i,V _j>.

V _i表示 X _i 的隐向量,  V _j 表示 X _j 的隐向量

为了求出 W _i,j, 我们对每一个特征分量 X_i 引入辅助向量

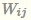然后，利用 对  进行求解。对辅助向量的维度k值的限定，反映了FM模型的表达能力。

那么ωij组成的矩阵可以表示为:

则FM的模型方程为：

则二次项的参数数量减少为kn个，远少于多项式模型的参数数量.我觉得上式应该是w _i,j = <v_i,v^T_j>,但是上面的写法才是对的，因为是点乘，两向量得是相同维度。还有i的取值为1到n-1,j的取值是i+1到n，因为特征不可能自己和自己组合

FM算法的求解过程：

我的理解：第一步是一个矩阵(矩阵中所有元素求和)减去对角线部分，然后除以2。多项式部分的计算复杂度是O(kn).即FM可以在线性时间对新样本作出预测

回归问题：最小均方误差(the least square error)  均方(一组数的平方的平均值)

二分类问题：对数损失函数，其中表示的是阶跃函数Sigmoid

对数损失是用于最大似然估计的，一组参数在一堆数据下的似然值，等于每一条数据的概率之积，而损失函数一般是每条数据的损失之和，为了把积变为和(我的理解：方便计算)，就取了对数。再加个负号是为了让最大似然值和最小损失对应起来(本来求和最大时对应的参数，加上负号后，求和最小时对应的参数，则等价于求最小损失)。

这个就是标准形式的对数损失函数，将sigmoid函数带入，符号抵消，即为log(1+exp(-yf(x)))

---

对于回归问题：可以理解为SGD,单样本训练

对于二分类问题：

       <=(由左式可知，Vi,f的训练只需要样本的Xi特征非0即可，适合于稀疏数据)

在使用SGD训练模型时，在每次迭代中，只需计算一次所有f的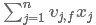，就能够方便得到所有V _i,f的梯度，(上述偏导结果求和公式中没有i,即与i无关，只与f有关)显然计算所有f的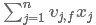的复杂度是O(kn),模型参数一共有nk + n + 1个。因此，FM参数训练的复杂度也是O(kn).综上可知，FM可以在线性时间训练和预测，是一种非常高效的模型。

我的理解：正则化系数用于衡量正则项与损失项的比重

总结：FM是一种比较灵活的模型，通过合适的特征变换方式，FM可以模拟二阶多项式核的SVM模型、MF模型、SVD++模型等。相比SVM的二阶多项式核而言，FM在样本稀疏的情况下是有优势的；而且，FM的训练/预测复杂度是线性的，而二项多项式核SVM需要计算核矩阵，核矩阵复杂度就是N平方。SVD++与MF类似，在特征的扩展性上都不如FM，在此不再赘述。

转自：

http://blog.csdn.net/itplus/article/details/40534923

http://blog.csdn.net/itplus/article/details/40536025

---

logistic回归两种形式：

第一种形式：label取值为0或1

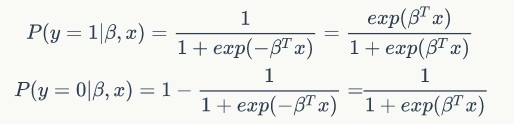
第二种形式：将label和预测函数放在一起，label取值为1或-1

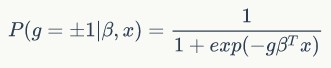
显然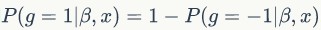，，上述两种形式等价。

第一种形式的分类法则：

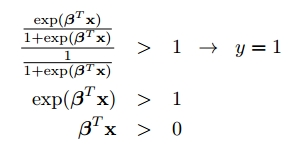
第二种形式的分类法则：

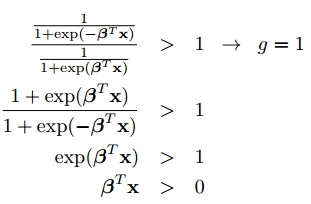
第一种形式的损失函数可由极大似然估计推出，对于第二种形式的损失函数（标准的对数损失函数形式，参考https://en.wikipedia.org/wiki/Loss_functions_for_classification 中的logistic  loss）,

 左式将分数倒过来，负号提出来，就得到常见的对数损失函数的形式

其中，

则loss最小化可表示为：

上式最后即为极大似然估计的表示形式，则logistic回归模型使用的loss函数为对数损失函数，使用极大似然估计的目的是为了使loss函数最小。

参考： https://www.zybuluo.com/frank-shaw/note/143260