51 NOD 1383 整数分解为2的幂
设f[i]为i这个数的划分方案,则:
1.i是奇数的时候,最前面只能放1,所以f[i] = f[i-1]
2.i是偶数的时候,最前面可以放1也可以不放1,而不放1的时候数列都是偶数所以 f[i] = f[i-1] + f[i>>1].
- #include<bits/stdc++.h>
- #define ll long long
- using namespace std;
- const int ha=1000000007;
- const int maxn=1000005;
- int f[maxn],n;
- inline int add(int x,int y){ x+=y; return x>=ha?x-ha:x;}
- inline void dp(){
- f[0]=1;
- for(int i=1;i<=n;i++)
- if(i&1) f[i]=f[i-1];
- else f[i]=add(f[i-1],f[i>>1]);
- }
- int main(){
- scanf("%d",&n);
- dp();
- printf("%d\n",f[n]);
- return 0;
- }
51 NOD 1383 整数分解为2的幂的更多相关文章
- 51Nod 1048 1383 整数分解为2的幂
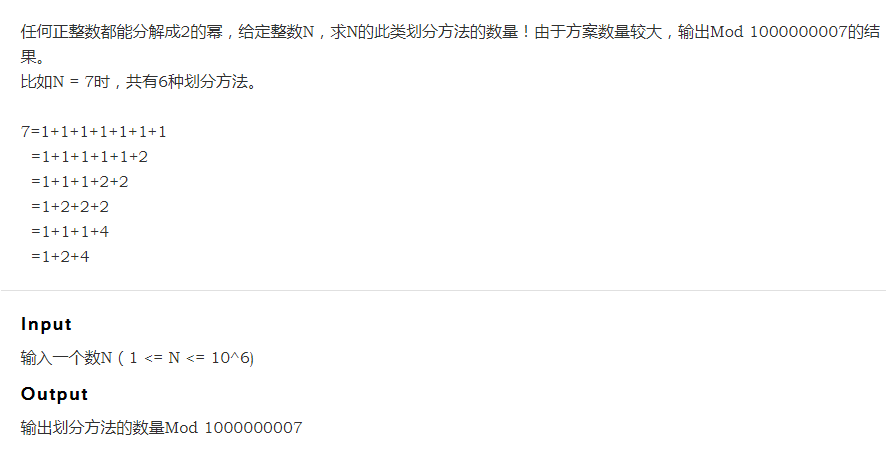
任何正整数都能分解成2的幂,给定整数N,求N的此类划分方法的数量! 比如N = 7时,共有6种划分方法. 7=1+1+1+1+1+1+1 =1+1+1+1+1+2 =1+1+1+2+2 ...
- [2022-2-18] OICLASS提高组模拟赛2 A·整数分解为2的幂
题目链接 问题 A: 整数分解为 2 的幂 题目描述 任何正整数都能分解成 2 的幂,给定整数 N,求 N 的此类划分方法的数量!由于方案数量较大,输出 Mod 1000000007 的结果. 比如 ...
- 51Nod 1048 整数分解为2的幂 V2
题目链接 分析: $O(N)$和$O(NlogN)$的做法很简单就不写了...%了一发神奇的$O(log^3n*$高精度$)$的做法... 考虑我们只能用$2$的整次幂来划分$n$,所以我们从二进制的 ...
- [51nod1383&1048]整数分解为2的幂:DP
算法一 分析 \(f[x]=f[x-1]+f[x/2] \times [x \equiv 0 \mod 2],O(n)\) 代码 n=int(input()) f=[0]*(n+5) f[0]=1 m ...
- 51 nod 1439 互质对(Moblus容斥)
1439 互质对 题目来源: CodeForces 基准时间限制:2 秒 空间限制:131072 KB 分值: 160 难度:6级算法题 有n个数字,a[1],a[2],…,a[n].有一个集合,刚开 ...
- 51 nod 1427 文明 (并查集 + 树的直径)
1427 文明 题目来源: CodeForces 基准时间限制:1.5 秒 空间限制:131072 KB 分值: 160 难度:6级算法题 安德鲁在玩一个叫“文明”的游戏.大妈正在帮助他. 这个游 ...
- 51 nod 1421 最大MOD值
1421 最大MOD值 题目来源: CodeForces 基准时间限制:1 秒 空间限制:131072 KB 分值: 80 难度:5级算法题 有一个a数组,里面有n个整数.现在要从中找到两个数字(可以 ...
- 51 nod 1405 树的距离之和
1405 树的距离之和 基准时间限制:1 秒 空间限制:131072 KB 分值: 40 难度:4级算法题 给定一棵无根树,假设它有n个节点,节点编号从1到n, 求任意两点之间的距离(最短路径)之 ...
- 51 nod 1610 路径计数(Moblus+dp)
1610 路径计数 基准时间限制:1 秒 空间限制:131072 KB 分值: 80 难度:5级算法题 路径上所有边权的最大公约数定义为一条路径的值. 给定一个有向无环图.T次修改操作,每次修改一 ...
随机推荐
- UEditor1.4.3的实例程序
官网:http://ueditor.baidu.com/website/ 配置下就可以使用 (1)下载,解压后文件结构如下: (2)将整个文件夹改名ueditor后复制到WebRoot目录下: (3) ...
- 四. python网络编程
第八章.网络基础知识 1. TCP/IP协议介绍 1.TCP/IP概念 TCP/IP: Transmission Control Protocol/Internet Protocol的简写,中译名为传 ...
- 请大神看看10.10Beta1的AppleRTC怎么破?原版会导致BIOS重置!
看起来 跟10.9一样 sudo perl -pi -e 's|\x75\x2e\x0f\xb6|\xeb\x2e\x0f\xb6|' /System/Library/Extensions/Apple ...
- windows10锁定屏幕聚焦图片导出
打开运行,输入%LocalAppData%\Packages\Microsoft.Windows.ContentDeliveryManager_cw5n1h2txyewy\LocalState\Ass ...
- redis:高可用分析
https://www.cnblogs.com/xuning/p/8464625.html 基于内存的Redis应该是目前各种web开发业务中最为常用的key-value数据库了,我们经常在业务中用其 ...
- mysql 导入数据库
1:创建数据库 dos 进入 xxx\MySQL5.7\bin 目录(很多人喜欢把这个路径配置在环境变量path中,这样在dos敲命令时,就直接是mysql......) mysql -uroot - ...
- 【STL】栈+队列+优先队列(详)+ 拯救行动题解
一.栈 栈(stack)又名堆栈,它是一种运算受限的线性表.其限制是仅允许在表的一端进行插入和删除运算.这一端被称为栈顶,相对地,把另一端称为栈底.向一个栈插入新元素又称作进栈.入栈或压栈,它是把新元 ...
- Java中HashMap底层原理源码分析
在介绍HashMap的同时,我会把它和HashTable以及ConcurrentHashMap的区别也说一下,不过本文主要是介绍HashMap,其实它们的原理差不多,都是数组加链表的形式存储数据,另外 ...
- PAT Basic 1038
1038 统计同成绩学生 本题要求读入N名学生的成绩,将获得某一给定分数的学生人数输出. 输入格式: 输入在第1行给出不超过10^5^的正整数N,即学生总人数.随后1行给出N名学生的百分制整数成绩,中 ...
- Python学习案例
例1.求101到200之间所有的质数,并打印总数. 说明:除去1和它本身之外,不能被其他数整除,就是质数. #!/bin/python #-*- coding:utf-8 -*- #使用集合法 l = ...
