求导四则运算以及三角函数求导 Derivative formulas

对特定函数的求导。

---

1：sin（x） 对其进行求斜率。带入公式得：[ sin（x+Δx）- sin（x）]/Δx  = [ sinx*cosΔx + cosx*sinΔx -sin x ]/ Δx = [ cos x * sin Δx ] / Δx = cos x

　　　　cos Δx = 1 当 Δx无限趋近于0 的时候 ，sin x和x在 0点是一样的，其取值也一样。

2：cos（x）求其斜率（导数）[ cox(x+Δx) - cos x ]/ Δx = [ cos x*cos Δx - sin x*sin Δx -cos x ] / Δx = ( - sin x*sin Δx ) / Δx  = - sin x

　　　　cos Δx = 1 当 Δx无限趋近于0 的时候 ，sin x和x在 0点是一样的，其取值也一样。

Remark

　　　　     可以看出 ， 求cos x 在 0 处的导数 ， 用极限去求根据点斜式。

一直以来的疑问：

　　问什么可以认为 sin x / x 当x无限趋近于的时候可以认为其值为 1 呢 ？我们用几何进行证明。

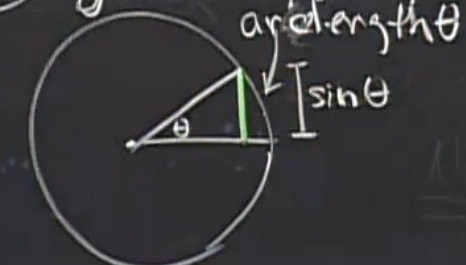　　　　　　　　        为什么 sin Θ / Θ = 1 呢？在图中 sin Θ的值可以用 绿线的长度来表示 。 Θ 可以用Θ角所对应的圆上面的那一段弧线来表示 ， 当 Θ 角趋近于无穷小的时候，sin Θ 和 Θ弧，接近重合 所以可以认为 sin Θ / Θ = 1

我们在这之前所说的所有的内容的都是根据 点斜式和上面的理论进行推导而来的。

---

通用求导法则