数据结构 - 顺序栈的实行（C语言）

一、什么是栈？

在我们软件应用中，栈这种后进先出数据结构的应用是非常普遍的。比如 Word、 Photoshop 等文档或图像编辑软件中， 都有撤销（undo）的操作，也是用栈这种方式来实现的。

栈(stack)是限定仅在表尾进行插入和删除操作的线性表。

我们把允许插入和删除的一端称为栈顶(top)，另一端称为栈底(bottom)，不含任何数据元素的栈称为空栈。 栈又称为后进先出（Last In Filrst Out) 的线性表，简称 LlFO 结构。

栈的插入操作，叫作进栈，也称压栈、入栈。类似子弹入弹夹，如下图-左所示。栈的删除操作，叫作出栈，也有的叫作弹栈。

二、什么是顺序栈？

顺序栈：是指利用顺序存储结构实现的栈。线性栈可以用数组来实现，对于栈这种只能一头插入删除的线性表来说，用数组哪一端来作为栈顶和栈底比较好？

对，没错，下标为 0 的一端作为栈底比较好，因为首元素都存在栈底，变化最小，所以让它作栈底。我们定义一个 top 变量来指示栈顶元素在数组中的位置，若存储栈的长度为 StackSize，则栈顶位置 top 必须小于 StackSize。当栈存在一个元素时，top 等于 0，因此通常把空栈的判定条件定为 top 等于 -1。

来看栈的结构定义：

typedef int ElemType; /* ElemType类型根据实际情况而定，这里假设为int */

/* 顺序栈结构 */
typedef struct
{
	ElemType data[MAXSIZE];
    int top; /* 用于栈顶指针 */
}SeqStack;

若现在有一个栈，StackSize 是 5，则栈普通情况、空栈和栈满的情况示意图如下图所示：

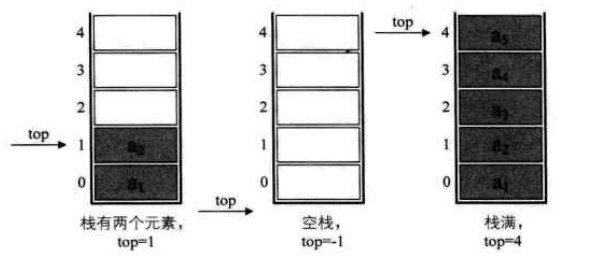
• 栈空时：栈顶指针（top）= -1；
• 栈满时：栈顶指针（top）= MAXSIZE-1；
• 栈未满：就是栈中存在元素，top 指针还未达到 MAXSIZE-1。

三、基本操作

3.1 初始化栈操作

实现代码如下：

// 初始化栈操作
Status initStack(SeqStack **stack)
{
	*stack = (SeqStack *)malloc(sizeof(SeqStack));
	(*stack)->top = -1;

	return TRUE;
}

3.2 进栈操作

进栈的示意图如下：

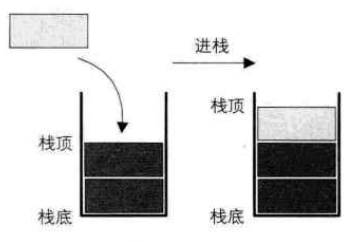
实现进栈只需要两步：

• 判断栈是否已经满了，如果满了当然就入不了栈。
• 栈顶指针 +1，在新栈顶位置存入要进栈的元素。

实现代码如下：

// 进栈操作
Status push(SeqStack *stack, const ElemType e)
{
	if (stack->top == MAXSIZE - 1) // 判断是否栈满
	{
		return FALSE;
	}
	stack->top++; // 栈顶指针加1
	stack->data[stack->top] = e; // 将新插入元素赋值给栈顶空间

	return TRUE;
}

3.3 出栈操作

出栈的示意图如下：

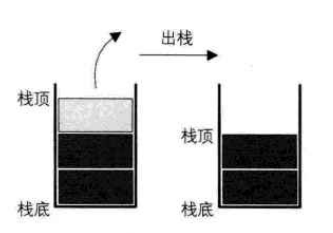
实现出栈也只需要两步：

• 判断栈是否为空，里面没有数据先出栈也没有。
• 将栈顶元素出栈，栈顶指针 -1。

实现代码如下：

// 出栈操作
Status pop(SeqStack *stack, ElemType *e)
{
	if (stack->top == -1) // 判断是否空栈
		return FALSE;

	*e = stack->data[stack->top];   // 将要删除的栈顶元素赋值给e
	stack->top--;               // 栈顶指针减1

	return TRUE;
}

3.4 遍历栈操作

实现代码如下：

// 遍历栈操作
Status traverseStack(SeqStack *stack)
{
	for (int i = 0; i <= stack->top; i++)
		printf("%d ", stack->data[i]);
	printf("\n");

	return TRUE;
}

四、完整程序

#include <stdio.h>
#include <stdlib.h> 

#define TRUE 1
#define FALSE 0
#define MAXSIZE 20 /* 存储空间初始分配量 */

typedef int Status;
typedef int ElemType; /* ElemType类型根据实际情况而定，这里假设为int */

/* 顺序栈结构 */
typedef struct
{
	ElemType data[MAXSIZE];
	int top; /* 用于栈顶指针 */
}SeqStack;

Status initStack(SeqStack **stack); // 初始化栈操作
Status push(SeqStack *stack, const ElemType e); // 进栈操作
Status pop(SeqStack *stack, ElemType *e); // 出栈操作
Status traverseStack(SeqStack *stack); // 遍历栈操作
Status clearStack(SeqStack *stack); // 清空栈操作
Status isEmpty(SeqStack *stack); // 判断是否为空
Status getTop(SeqStack *stack, ElemType *e); // 获得栈顶元素
int getLength(SeqStack *stack); // 获取栈的长度

// 初始化栈操作
Status initStack(SeqStack **stack)
{
	*stack = (SeqStack *)malloc(sizeof(SeqStack));
	(*stack)->top = -1;

	return TRUE;
}

// 进栈操作
Status push(SeqStack *stack, const ElemType e)
{
	if (stack->top == MAXSIZE - 1) // 判断是否栈满
	{
		return FALSE;
	}
	stack->top++; // 栈顶指针加1
	stack->data[stack->top] = e; // 将新插入元素赋值给栈顶空间

	return TRUE;
}

// 出栈操作
Status pop(SeqStack *stack, ElemType *e)
{
	if (stack->top == -1) // 判断是否空栈
		return FALSE;

	*e = stack->data[stack->top];   // 将要删除的栈顶元素赋值给e
	stack->top--;               // 栈顶指针减1

	return TRUE;
}

// 遍历栈操作
Status traverseStack(SeqStack *stack)
{
	for (int i = 0; i <= stack->top; i++)
		printf("%d ", stack->data[i]);
	printf("\n");

	return TRUE;
}

// 清空栈操作
Status clearStack(SeqStack *stack)
{
	stack->top = -1;

	return TRUE;
}

// 判断是否为空
Status isEmpty(SeqStack *stack)
{
	return stack->top == -1 ? TRUE : FALSE;
}

// 获得栈顶元素
Status getTop(SeqStack *stack, ElemType *e)
{
	if (stack->top == -1)
		return FALSE;
	else
		*e = stack->data[stack->top];

	return TRUE;
}

// 获取栈的长度
int getLength(SeqStack *stack)
{
	return stack->top + 1;
}

int main()
{
	// 初始化栈
	SeqStack *stack;
	if (initStack(&stack) == TRUE)
		printf("初始化顺序栈成功！\n\n");

	// 入栈操作
	for (int j = 1; j <= 10; j++)
		push(stack, j);
	printf("入栈操作（0-10）!\n\n");

	// 出栈操作
	int e;
	pop(stack, &e);
	printf("弹出的栈顶元素e=%d\n\n", e);

	// 遍历栈
	printf("遍历栈，栈中元素依次为：");
	traverseStack(stack);
	printf("\n");

	// 获得栈顶元素
	getTop(stack, &e);
	printf("栈顶元素 e=%d 栈的长度为%d\n\n", e, getLength(stack));

	// 判断是否为空栈
	printf("栈空否：%d(1:空 0:否)\n\n", isEmpty(stack));

	// 清空栈
	clearStack(stack);
	printf("清空栈后，栈空否：%d(1:空 0:否)\n\n", isEmpty(stack));

	return 0;
}

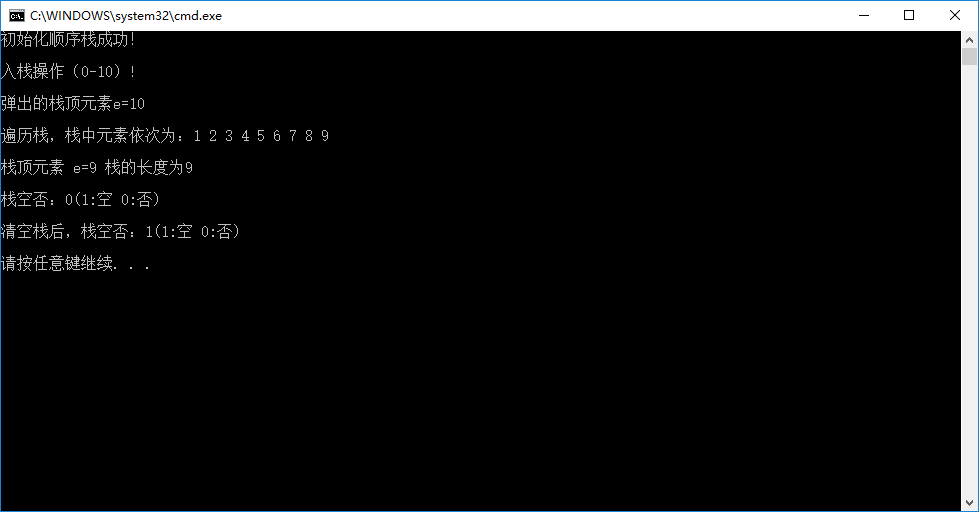
输出结果如下图所示：

参考：

《大话数据结构 - 第4章》 栈与队列