P3371 【模板】单源最短路径（弱化版）（Dijkstra算法）

题目描述

如题，给出一个有向图，请输出从某一点出发到所有点的最短路径长度。

输入输出格式

输入格式：

第一行包含三个整数N、M、S，分别表示点的个数、有向边的个数、出发点的编号。

接下来M行每行包含三个整数Fi、Gi、Wi，分别表示第i条有向边的出发点、目标点和长度。

输出格式：

一行，包含N个用空格分隔的整数，其中第i个整数表示从点S出发到点i的最短路径长度（若S=i则最短路径长度为0，若从点S无法到达点i，则最短路径长度为2147483647）

输入输出样例

输入样例#1： 复制

4 6 1
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4

输出样例#1： 复制

0 2 4 3

说明

时空限制：1000ms,128M

数据规模：

对于20%的数据：N<=5，M<=15；

对于40%的数据：N<=100，M<=10000；

对于70%的数据：N<=1000，M<=100000；

对于100%的数据：N<=10000，M<=500000。保证数据随机。

对于真正 100% 的数据，请移步 P4779。请注意，该题与本题数据范围略有不同。

样例说明：

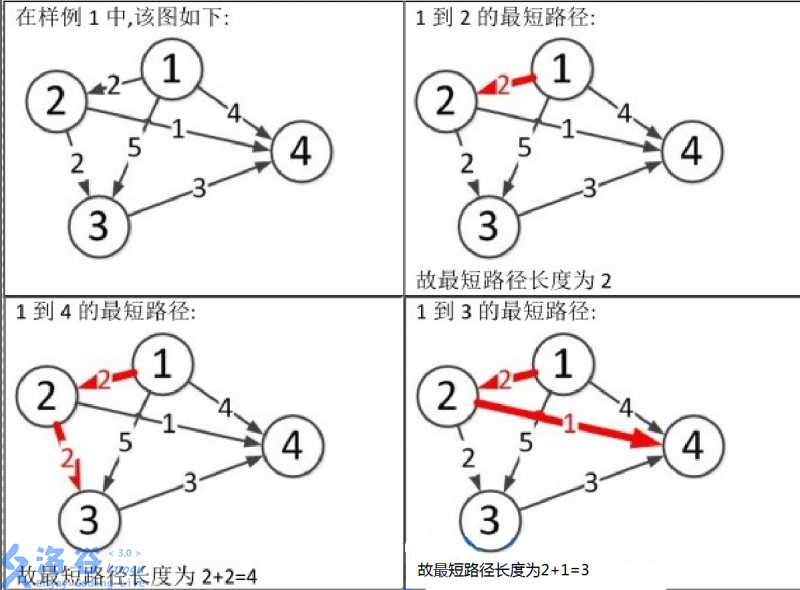
图片1到3和1到4的文字位置调换

wa到自闭了 pair 和 make_pair 搞不清 有毒

 //单源最短路径2Dijkstra算法
 #include <iostream>
 #include <string>
 #include <cstring>
 #include <vector>
 #include <queue>
 #include <cstdio>
 #include <utility>
 using namespace std;
 typedef long long ll;
 typedef pair<int,int> P;
 const int INF=;
 struct edge
 {
     int from,to,cost;
 }es[];
 vector<int> G[];
 int d[];
 int n,m,s;//n顶点数，m边数，s起点
 int main()
 {
        scanf("%d%d%d",&n,&m,&s);
     for(int i=;i<=m;i++){
         scanf("%d%d%d",&es[i].from,&es[i].to,&es[i].cost);
         G[es[i].from].push_back(i);
     }
     for(int i=;i<=n;i++) d[i]=INF;
     priority_queue<P, vector<P>, greater<P> > que;
     d[s]=;
     que.push(make_pair(,s));
     while(!que.empty()){
         P p=que.top();
         que.pop();
         int v=p.second;
         if(d[v]!=p.first) continue;
         for(int i=;i<G[v].size();++i){
             edge e=es[G[v][i]];
             if(d[e.to]>d[v]+e.cost){
                 d[e.to]=d[v]+e.cost;
                 que.push(make_pair(d[e.to],e.to));
             }
         }
     }
     for(int i=;i<=n;i++) printf("%d ",d[i]);
     return ;
 }