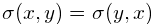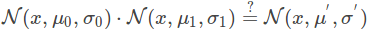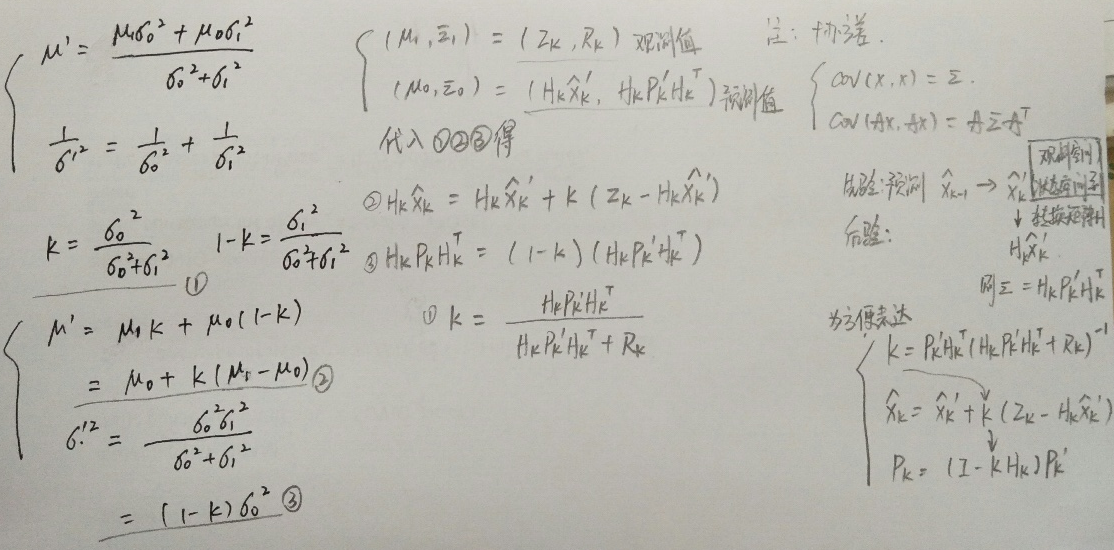kalman滤波(二)---扩展kalman滤波[EKF]的推导
一.状态估计的解释

我们知道每个方程都受噪声的影响,这里把位姿x和路标y看成服从某种概率分布的随机变量。因此我们关心的问题就变成了:当我们已知某些运动数据u和观测数据z时,如何确定状态量x,y的分布?比较常见且合理的情况下,我们假设状态量和噪声项服从高斯分布---这意味着在程序中只需存储它们的均值和协方差即可。均值可看作是对变量最优值的估计,而协方差矩阵度量了它的不确定性。如果认为k时刻状态只与k-1时刻状态有关,而与再之前无关,我们就会得到以卡尔曼滤波(EKF)为代表的滤波器方法,在滤波方法综合那个,我们会将某时刻的状态估计,推导到下一时刻;另一种方法考虑k时刻状态与之前所有状态的关系,将得到以非线性优化为主体的优化框架。目前SLAM的主流是非线性优化方法。
二.EKF
[1] 卡尔曼滤波 -- 从推导到应用(一)
卡尔曼滤波 -- 从应用(一) 到 (二)
|
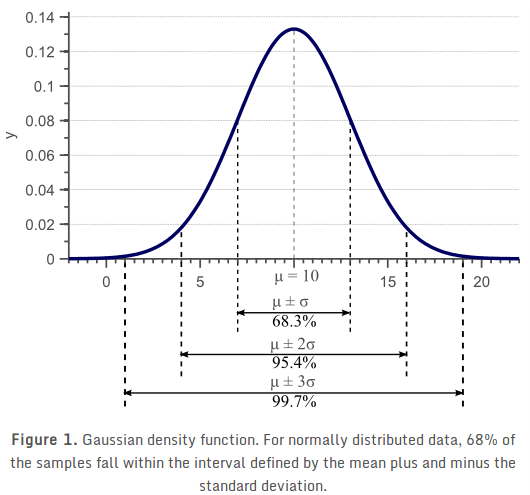
高斯分布,又称为正态分布: 
|
|
样本方差的无偏估计可以通过以下方式获得(μ为期望,即均值):
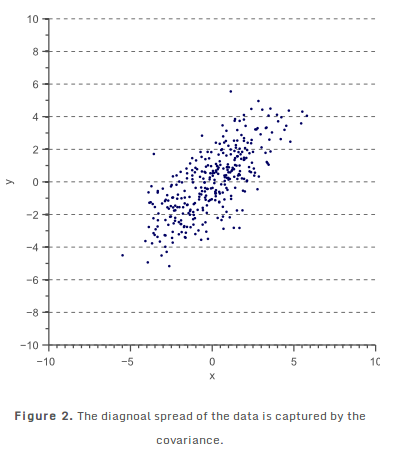
方差只能用来解释数据在与特征空间轴线平行的方向上的传播。图2所示的2d特征空间: 协方差: 协方差矩阵: 二维正态分布数据完全由均值和2×2协方差矩阵来解释。类似地,一个3×3的协方差矩阵用于捕捉三维数据的传播,而n×n次协方差矩阵捕捉n维数据的传播。
前两个:协方差对称,最大方差方向与轴不重合,并且数据被旋转。 后两个:协方差为0,最大方差方向是轴对齐 2.特征值分解Eigendecomposition of a covariance matrix 3.Covariance matrix as a linear transformation 协方差矩阵的特征向量的最直观的解释之一是,它们是数据变化最多的方向。(更准确地说,第一特征向量是数据变化最多的方向,第二特征向量是那些正交(垂直)到第一特征向量的最大方差的方向,第三个特征向量是与前两个正交的最大方差的方向,等等)。下面是2个维度的示例[ 1 ]:
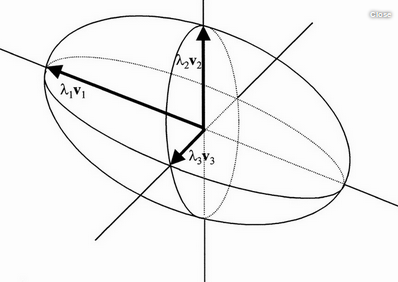
每个数据样本是一个2维点,坐标x,y。这些数据样本的协方差矩阵的特征向量是向量u和v;u,长箭头,是第一特征向量,v,短箭头,是第二个。(特征值是箭头的长度),正如你所看到的,第一个特征向量点(从数据的平均值)到数据在欧氏空间中变化最大的方向,第二特征向量是正交的(垂直的)到第一个。 在3个维度中可视化有点困难,但这里有一个尝试[ 2 ]:
在这种情况下,假设所有的数据点都位于椭球内。V1,方向的数据变化最大,是第一特征向量(λ1是相应的特征值)。V2是在那些与V1正交的方向上数据变化最大的方向。V3是那些方向与V1和V2正交的最大方差方向(虽然只有一个这样的正交方向)。 |
[2]卡尔曼滤波原理及实现---介绍的详细,适合初学者;卡尔曼增益K解释的较好
http://www.tina-vision.net/docs/memos/2003-003.pdf
|
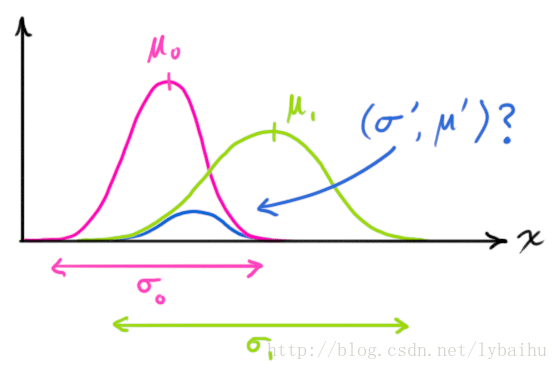
在求解卡尔曼增益的过程中: 对两个云团进行重叠,找到重叠最亮的点(实际上我们能够把云团看做一帧图像,这帧图像上面的每一个像素具有一个灰度值,灰度值大小代表的是该事件发生在这个点的概率密度),最亮的点,从直觉上面讲,就是以上两种预测准确的最大化可能性,也就是得到了最终的结果。非常神奇的事情是,对两个高斯分布进行乘法运算,得到新的概率分布规律仍然符合高斯分布,然后就取下图当中蓝色曲线峰值对应的横坐标不就是结果了嘛。证明如下: σ2 N(x,μ,σ)=1σ2π−−√e−(x−μ)22σ2(4
如果存在两个这样的高斯分布,只不过期望和方差不同,当两个分布相乘,得到什么结果? 是不是下式成立:
注意:我这里铅笔书写的标注和上面博客中的是反的,只要按步骤推导还是容易理解的。 N(x,μ0,σ0)⋅N(x,μ1,σ1)=?N(x,μ′,σ′)(5
|
kalman滤波(二)---扩展kalman滤波[EKF]的推导的更多相关文章
- (二). 细说Kalman滤波:The Kalman Filter
本文为原创文章,转载请注明出处,http://www.cnblogs.com/ycwang16/p/5999034.html 前面介绍了Bayes滤波方法,我们接下来详细说说Kalman滤波器.虽然K ...
- 学习 opencv---(7) 线性邻域滤波专场:方框滤波,均值滤波,高斯滤波
本篇文章中,我们一起仔细探讨了OpenCV图像处理技术中比较热门的图像滤波操作.图像滤波系列文章浅墨准备花两次更新的时间来讲,此为上篇,为大家剖析了"方框滤波","均值滤 ...
- OpenCV计算机视觉学习(4)——图像平滑处理(均值滤波,高斯滤波,中值滤波,双边滤波)
如果需要处理的原图及代码,请移步小编的GitHub地址 传送门:请点击我 如果点击有误:https://github.com/LeBron-Jian/ComputerVisionPractice &q ...
- Atitit 图像处理 平滑 也称 模糊, 归一化块滤波、高斯滤波、中值滤波、双边滤波)
Atitit 图像处理 平滑 也称 模糊, 归一化块滤波.高斯滤波.中值滤波.双边滤波) 是一项简单且使用频率很高的图像处理方法 用途 去噪 去雾 各种线性滤波器对图像进行平滑处理,相关OpenC ...
- Kalman Filter、Extended Kalman Filter以及Unscented Kalman Filter介绍
模型定义 如上图所示,卡尔曼滤波(Kalman Filter)的基本模型和隐马尔可夫模型类似,不同的是隐马尔科夫模型考虑离散的状态空间,而卡尔曼滤波的状态空间以及观测空间都是连续的,并且都属于高斯分布 ...
- 【滤波】标量Kalman滤波的过程分析和证明及C实现
摘要: 标量Kalman滤波的过程分析和证明及C实现,希望能够帮助入门的小白,同时得到各位高手的指教.并不涉及其他Kalman滤波方法. 本文主要参考自<A Introduction to th ...
- 卡尔曼(Kalman)滤波及十种数据采集滤波的方法和编程实例
卡尔曼(Kalman)滤波:https://blog.csdn.net/CSDN_X_W/article/details/90289021 十种数据采集滤波的方法和编程实例:https://wenku ...
- 目标跟踪之粒子滤波---Opencv实现粒子滤波算法
目标跟踪学习笔记_2(particle filter初探1) 目标跟踪学习笔记_3(particle filter初探2) 前面2篇博客已经提到当粒子数增加时会内存报错,后面又仔细查了下程序,是代码方 ...
- 实现Sobel算子滤波、Robers算子滤波、Laplace算子滤波
前几天,老师布置了这样一个任务,读取图片并显示,反色后进行显示:进行Sobel算子滤波,然后反色,进行显示:进行Robers算子滤波,然后反色,进行显示.我最后加上了Laplace算子滤波,进行了比较 ...
随机推荐
- node笔记汇总
项目依赖分两种,一个就是普通的项目依赖比如bootstrap,还用一种只是开发阶段需要用的,这种属于开发依赖比如gulp,开发依赖最终记录在devDependencies节点里面 - ...
- python 【winerror2】系统找不到指定的路径
# _*_ coding:utf-8_*_from selenium import webdriver driver = webdriver.Firefox()driver.get("htt ...
- easyUI默认图标的使用
使用格式如下: <table id="table" class="easyui-datagrid" style="width:600px;hei ...
- 关于java做题时需要注意的事项
1.要熟悉eclipse的使用 2.用java提交时只能有一个public class 且类名只能为Main 3.提交时不能提交包名 4.提交时要将引入的包一起提交 5.虽然java提供了很多的函数, ...
- 京东返利渠道,自己拿返利,无需A推B操作
京东返利渠道,自己拿返利,无需A推B操作,简单快捷方便 1.在微信小程序中搜索 “京东饭粒” 2.进入京东饭粒,进购物车下单(只能在购物车内下单返利) 3.收货后26天返京豆到你的京东账号中,”佛系返 ...
- 【spring】之xml和Annotation,Bean注入的方式
基于xml形式Bean注入 @Data @AllArgsConstructor @NoArgsConstructor public class PersonBean { private Integer ...
- 【OpenStack】相关概念
网络 network和subnet Service subnets: 创建network,subnet, instances 官方示例 Network components: Switches/ Ro ...
- Linux(CentOS-7) 下载 解压 安装 redis 操作的一些基本命令
使用xshell 连接到虚拟机,并且创建 一个redis目录:创建文件命令:mkdir 文件名ls:查看当前文件里面的所有文件 使用xftp 将下载的linux版本 reids上传动新建的redis目 ...
- 解决mysqli的中文乱码问题
有时候我们向服务器传汉字,出现内容为空,或???的问题,是因为mysqli对utf8的解码属于 Unicode码,会解析为 Unicode 码:所以我们要对内设置成gbk码, 尽管gbk码,很古来,但 ...
- 自己动手制作的淘宝闲鱼APP宝贝数据采集工具软件
之前做过淘宝PC端宝贝和店铺数据的采集,后来需要做APP端的数据采集,因为没有学过Android,以前也都是做PC端的软件,有没有其他方法呢? 突然想到了用手机模拟器,可以在电脑端控制运行手机APP端 ...

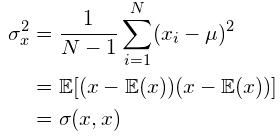
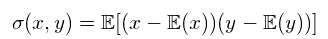
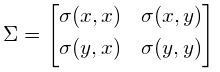 ,其中
,其中