P5280 [ZJOI2019]线段树

题目链接：洛谷

题目描述：【比较复杂，建议看原题】

---

这道题太神仙了，线段树上做树形dp。

根据树形dp的套路，都是按照转移的不同情况给节点分类。这里每次modify的时候对于节点的影响也不同，所以我们考虑分类。

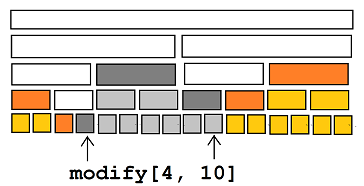
（这里借用一张图，%%%sooke大佬）

我们发现每次modify的时候对节点的影响有这5种节点。（因为每棵线段树的形态一致，所以我们只用一棵线段树）

一类点（白色）：在 modify 操作中，被半覆盖的点。

二类点（深灰）：在 modify 操作中，被全覆盖的点，并且能被遍历到。

三类点（橙色）：在 modify 操作中，未被覆盖的点，并且可以得到 pushdown 来的标记。

四类点（浅灰）：在 modify 操作中，被全覆盖的点，并且不能被遍历到。

五类点（黄色）：在 modify 操作中，未被覆盖的点，并且不可能得到 pushdown 来的标记。

设编号为$x$的节点，在$i$次modify之后，生成的这$2^i$棵线段树中，有$f_{x,i}$棵在这个节点上有标记.

我们对于每一类都推一下。

一类点：因为没有全覆盖，所以新的这些线段树在$x$上是没有标记的。所以$f_{x,i}=f_{x,i-1}+0$

二类点：因为全覆盖了，所以新的这些线段树在$x$上必有标记。所以$f_{x,i}=f_{x,i-1}+2^{i-1}$

三类点：因为要pushdown，所以$x$上有标记当且仅当之前的线段树中$x$及$x$的祖先至少有一个有标记。所以$f_{x,i}=f_{x,i-1}+\ldots$.

Oh,no！出锅了，这里不知道要加多少。

但是仔细一想，发现其实这个也是可以dp的。

---

设编号为$x$的节点，在$i$次modify之后，生成的这$2^i$棵线段树中，在$x$及$x$的祖先上，没有一个有标记的线段树有$g_{x,i}$棵。

然后继续推。

一类点：对于$g$，因为没有全覆盖，所以$x$和$x$的祖父也是没有标记的。

$$f_{x,i}=f_{x,i-1}+0,g_{x,i}=g_{x,i-1}+2^{i-1}$$

二类点：对于$g$，因为全覆盖了，所以$x$必定有标记。

$$f_{x,i}=f_{x,i-1}+2^{i-1},g_{x,i}=g_{x,i-1}+0$$

三类点：对于$g$，因为未被覆盖，所以对$x$及$x$的祖先并没有影响。

$$f_{x,i}=f_{x,i-1}+2^{i-1}-g_{x,i-1},g_{x,i}=g_{x,i-1}+g_{x,i-1}$$

四类点：对于$f$，因为没有被遍历到，所以对$x$的标记没有影响；对于$g$，因为被全覆盖，所以祖先上必定有标记。

$$f_{x,i}=f_{x,i-1}+f_{x,i-1},g_{x,i}=g_{x,i-1}+0$$

五类点：$f$同四类点；对于$g$，因为没有被覆盖，所以祖先上必定没有标记。

$$f_{x,i}=f_{x,i-1}+f_{x,i-1},g_{x,i}=g_{x,i-1}+g_{x,i-1}$$

初值：$f_{x,0}=0,g_{x,0}=1$

答案是整个线段树所有节点$f$之和，也可以用线段树顺便维护。

但是如果暴力转移就肯定是$O(n)$的，但其实比较复杂的一、二、三类点都至多有$O(\log n)$个，而四、五类点都是区间乘法就行。所以前者暴力转移，后者直接打懒标记。

---

如果您看得一脸懵逼（我的语文太差），那么看下面。

这里说的对点分类，是按照每一步操作（modify）对每个节点状态的影响（dp转移方程）来分类的。

所以类别并不属于dp状态的一维，只是一个分类讨论的过程。（通常的树形dp都是这个思路，大家可以好好理解一下）

如果您还是看不懂，那就可以看代码了。

 #include<cstdio>
 #define Rint register int
 using namespace std;
 typedef long long LL;
 const int N = , mod = ;
 inline int add(int a, int b){int res = a + b; if(res >= mod) res -= mod; return res;}
 inline int dec(int a, int b){int res = a - b; if(res < ) res += mod; return res;}
 int n, m, k = , f[N], g[N], lf[N], lg[N], sf[N];
 inline void pushf(int x, int val = ){
     f[x] = (LL) f[x] * val % mod;
     lf[x] = (LL) lf[x] * val % mod;
     sf[x] = (LL) sf[x] * val % mod;
 }
 inline void pushg(int x, int val = ){
     g[x] = (LL) g[x] * val % mod;
     lg[x] = (LL) lg[x] * val % mod;
 }
 inline void pushdown(int x){
     if(lf[x] != ) pushf(x << , lf[x]), pushf(x <<  | , lf[x]), lf[x] = ;
     if(lg[x] != ) pushg(x << , lg[x]), pushg(x <<  | , lg[x]), lg[x] = ;
 }
 inline void pushup(int x){
     sf[x] = add(sf[x << ], add(sf[x <<  | ], f[x]));
 }
 inline void build(int x, int L, int R){
     g[x] = lf[x] = lg[x] = ;
     if(L == R) return;
     int mid = L + R >> ;
     build(x << , L, mid);
     build(x <<  | , mid + , R);
 }
 inline void modify(int x, int L, int R, int l, int r){
     pushdown(x);
     if(l <= L && R <= r){
         f[x] = add(f[x], k);
         pushf(x << ); pushf(x <<  | );
         pushup(x);
         return;
     }
     int mid = L + R >> , lx = x << , rx = x <<  | ;
     g[x] = add(g[x], k);
     if(r <= mid){
         modify(lx, L, mid, l, r);
         pushdown(rx);
         f[rx] = add(f[rx], dec(k, g[rx]));
         g[rx] = add(g[rx], g[rx]);
         pushf(rx << ); pushf(rx <<  | );
         pushg(rx << ); pushg(rx <<  | );
         pushup(rx);
     } else if(mid < l){
         modify(rx, mid + , R, l, r);
         pushdown(lx);
         f[lx] = add(f[lx], dec(k, g[lx]));
         g[lx] = add(g[lx], g[lx]);
         pushf(lx << ); pushf(lx <<  | );
         pushg(lx << ); pushg(lx <<  | );
         pushup(lx);
     } else {
         modify(lx, L, mid, l, r);
         modify(rx, mid + , R, l, r);
     }
     pushup(x);
 }
 int main(){
     scanf("%d%d", &n, &m);
     build(, , n);
     for(Rint i = ;i <= m;i ++){
         int opt, l, r;
         scanf("%d", &opt);
         if(opt == ) printf("%d\n", sf[]);
         else {
             scanf("%d%d", &l, &r);
             modify(, , n, l, r); k = add(k, k);
         }
     }
 }

Luogu5280