【算法】二叉查找树(BST)实现字典API
二叉查找树的定义


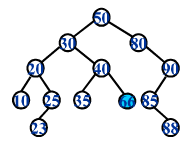

一颗二叉查找树对应一个有序序列
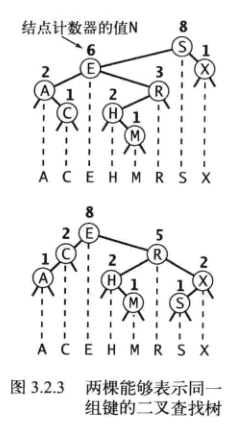

本文的字典API
int size() 获取字典中键值对的总数量
void put(int key, int val) 将键值对存入字典中
int get(int key) 获取键key对应的值
void delete(int key) 从字典中删去对应键(以及对应的值)
int min() 字典中最小的键
int max() 字典中最大的键
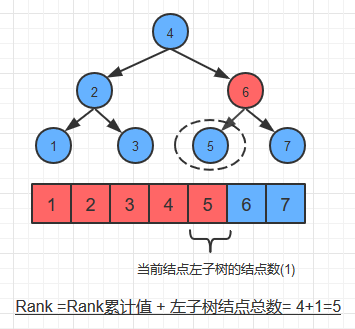
int rank(int key) key在键中的排名(小于key的键的数量)
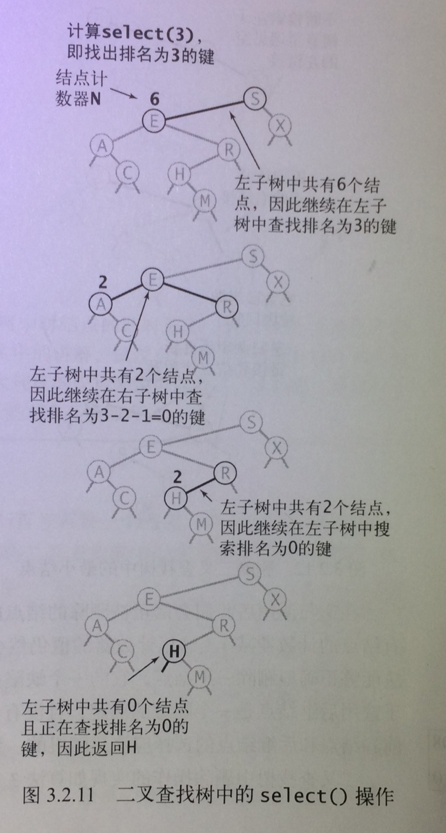
int select(int k) 获取排名为k的键
BST类的基本结构
public class BST {
Node root; // 根结点
private class Node { // 匿名内部类Node
int key; // 存储字典的键
int val; // 存储字典的值
Node left,right; // 分别表示左链接和右链接
int N; // 以该结点为根的子树中的结点总数
public Node (int key,int val,int N) {
this.key = key;
this.val = val;
this.N = N;
}
}
public int get (int key) { }
public void put (int key,int val) { }
// 其他方法 ... ...
}
Node内部类中成员变量N的作用


- 如果你不需要rank/select方法, 那么N完全可以设为BST的成员变量, 表示的是整棵树的结点总数, 维护N的代码编写很简单:在调用put方法时候使其加1, 在调用delete方法时使其减1。
- 如果你需要rank/select方法,则需对每个结点单独设N,代表的是该结点为根的子树中的结点总数,维护N的代码编写将会复杂很多,但这是必要的。(具体往下看)
方法设计的共同点
// 针对某个结点设计的递归处理方法
private int get(Node x, int key) {
// 递归调用get方法
}
// 将root作为上面方法的参数,从根结点开始处理整颗二叉树
public int get(int key) {
return get(root, key)
}
size方法
private int size (Node x) {
if(x == null) return 0;
return x.N;
}
public int size () {
return size(root);
}
- 当结点存在的时候,返回结点所在子树的结点总数(包括自身)
- 当结点不存在的时候,即x为null时,返回0
get方法
- key小于当前结点的键,说明key在左子树,向左儿子递归调用get
- key大于当前结点的键,说明key在右子树,向右儿子递归调用get
- key等于当前结点的键,查找成功并返回对应的值
- 查找到给定的key,返回对应的值
- x迭代至最下方的结点也没有查找到key,因为x.left=x.right=null,在下一次调用get返回-1,结束递归
private int get (Node x,int key) {
if(x == null) return -1; // 结点为空, 未查找到
if(key<x.key) {
return get(x.left,key); // 键在左子树,向左子树查找
}else if(key>x.key) {
return get(x.right, key); // 键在右子树,向右子树查找
}else{
return x.val; // 查找成功,返回值
}
}
public int get (int key) {
return get(root,key);
}

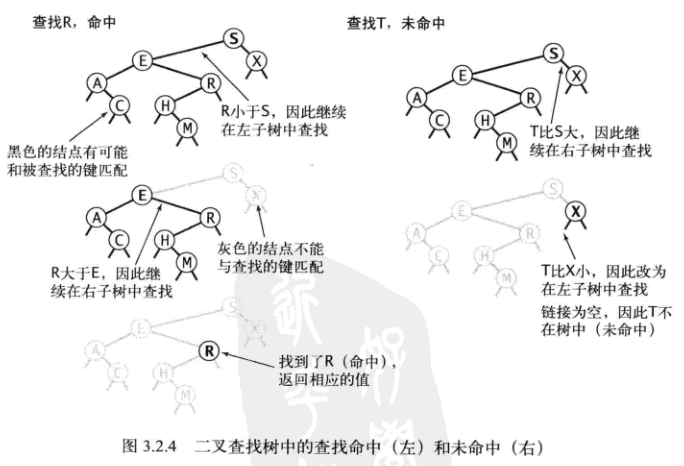
put方法
- key小于当前结点的键,向左子树插入
- key大于当前结点的键,向右子树插入
- key等于当前结点的键,则将值替换为给定的val
private Node put (Node x, int key, int val) {
if(x == null) return new Node(key,val,1); // 未查找到key,创建新结点,并插入树中
if(key<x.key){
x.left = put(x.left,key,val); // 向左子树插入
}else if(key>x.key){
x.right = put(x.right,key,val); // 向右子树插入
}else {
x.val = val; // 查找到给定key, 更新对应val
}
x.N =size(x.left) + size(x.right) + 1; // 更新结点计数器
return x; //
}
public void put (int key,int val) {
if(root == null) root = put(root,key,val); // 向空树中插入第一个结点
put(root,key,val);
}


x.N =size(x.left) + size(x.right) + 1; // 更新结点计数器
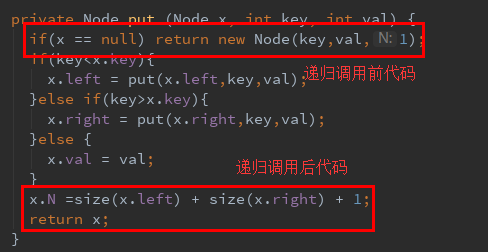

- 递归调用前代码先执行, 而递归调用后代码后执行
- 递归调用前代码是一个“沿着树向下走”的过程,即递归层次是由浅到深, 而递归调用后代码是一个“沿着树向上爬”的过程, 即递归层次是由深到浅
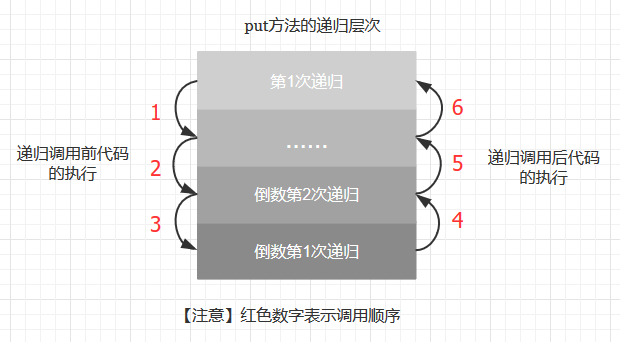


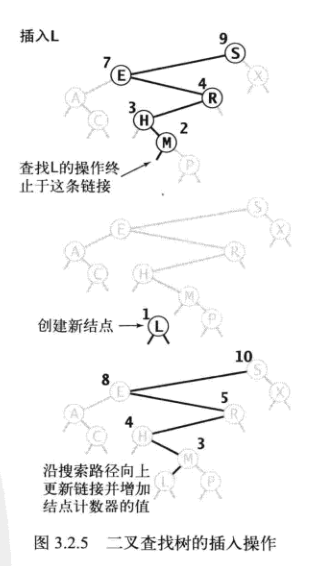
- 先“沿着树向下走”, 插入或更新结点
- 再“沿着树向上爬”, 更新结点计数器N
min,max方法

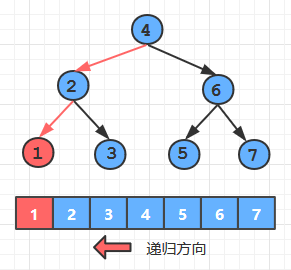
private Node min (Node x) {
if(x.left == null) return x; // 如果左儿子为空,则当前结点键为最小值,返回
return min(x.left); // 如果左儿子不为空,则继续向左递归
}
public int min () {
if(root == null) return -1;
return min(root).key;
}
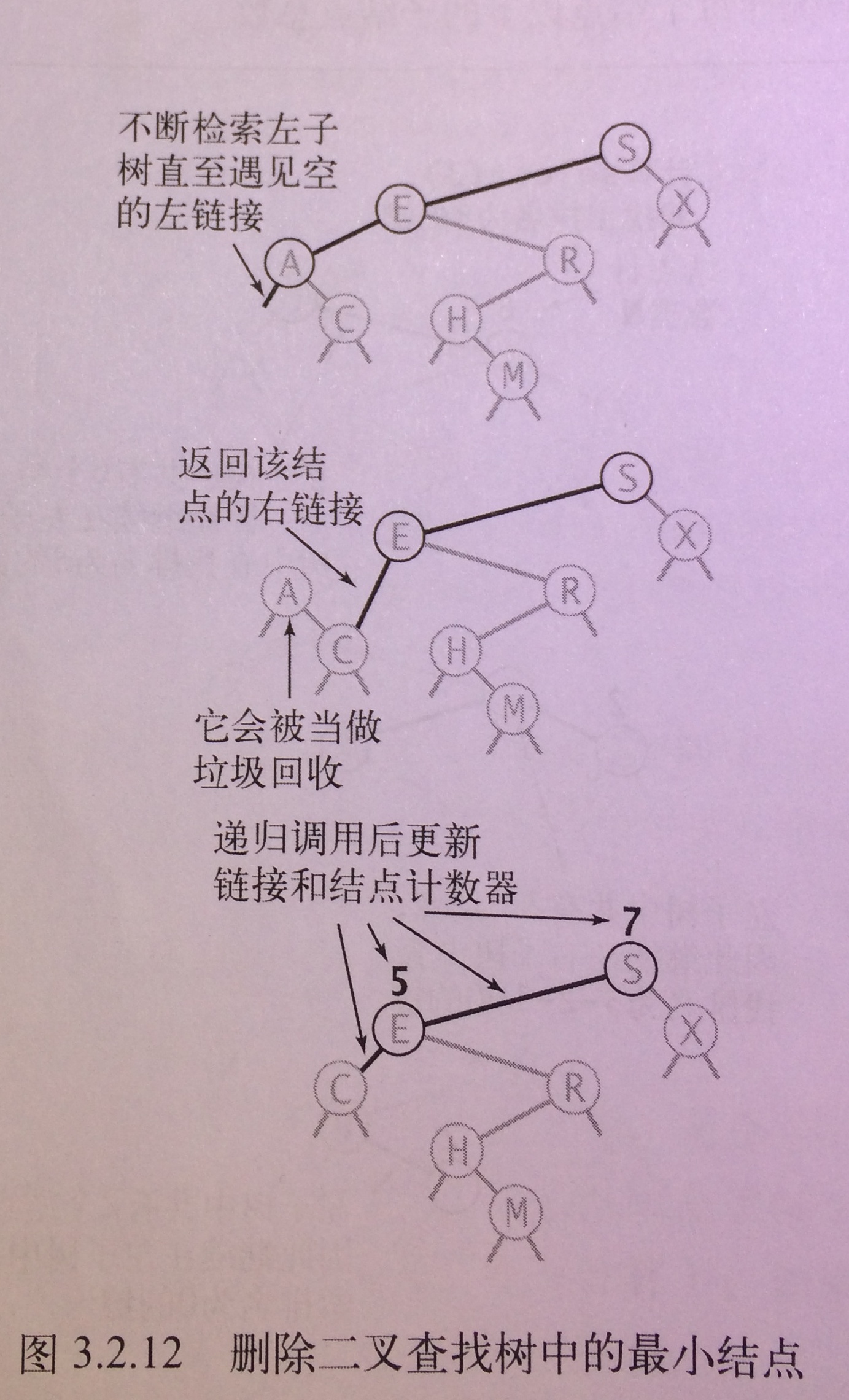
deleteMin方法
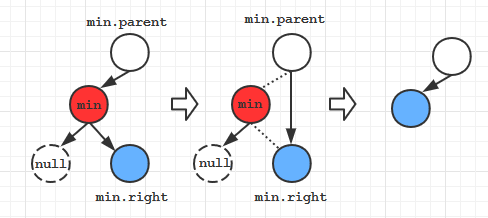

public Node deleteMin (Node x) {
if(x.left==null) return x.right; // 如果当前结点左儿子空,则将右儿子返回给上一层递归的x.left
x.left = deleteMin(x.left);// 向左子树递归, 同时重置搜索路径上每个父结点指向左儿子的链接
x.N = size(x.left) + size(x.right) + 1; // 更新结点计数器N
return x; // 当前结点不是min ###
}
public void deleteMin () {
root = deleteMin(root);
}
- 沿搜索路径重置结点链接
- 更新路径上的结点计数器
- 在递归到最后一个结点前, 下一层递归返回值是x(代码中###处), 这时,对上一层递归来说, x.left = deleteMin(x.left)等同于x.left = x.left
- 当递归到最后一个结点时,下一层递归中x = min, x.left==null判定为true, 返回x.right给上一层递归, 对上一层递归来说,x.left = deleteMin(x.left)等同于x.left = x.left.right;

delete方法






- 相对于父节点(A)而言是有序的。
- 相对于左子树(B)而言是有序的(15原本位于14右子树,所以大于14的左子树)
- 相对于右子树(C)而言是有序的(15是原来14右子树的最小键,移动后也小于C中其他结点)
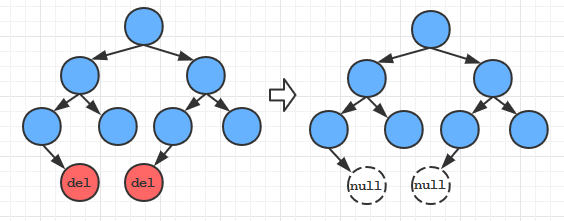
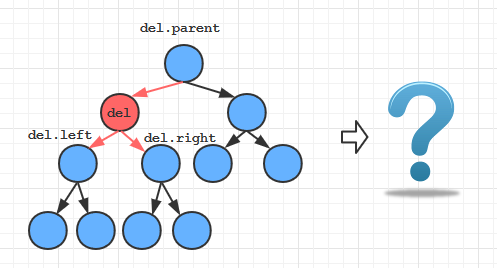
- 查找到相应的结点
- 将其删除






public Node delete (int key,Node x) {
if(x == null) return null;
if(key<x.key){
x.left = delete(key,x.left); // 向左子树查找键为key的结点 #1
}else if (key>x.key){
x.right = delete(key,x.right); // 向右子树查找键为key的结点 #2
}else{ // 在这个else里结点已经被找到,就是当前的x
// 这里处理的是上述的 第一种情况和第二种情况:左子树为null或右子树为null(或都为null)
if(x.left==null) return x.right; // 如果左子树为空,则将右子树赋给父节点的链接 #3
if(x.right==null) return x.left; // 如果右子树为空,则将左子树赋给父节点的链接 #4
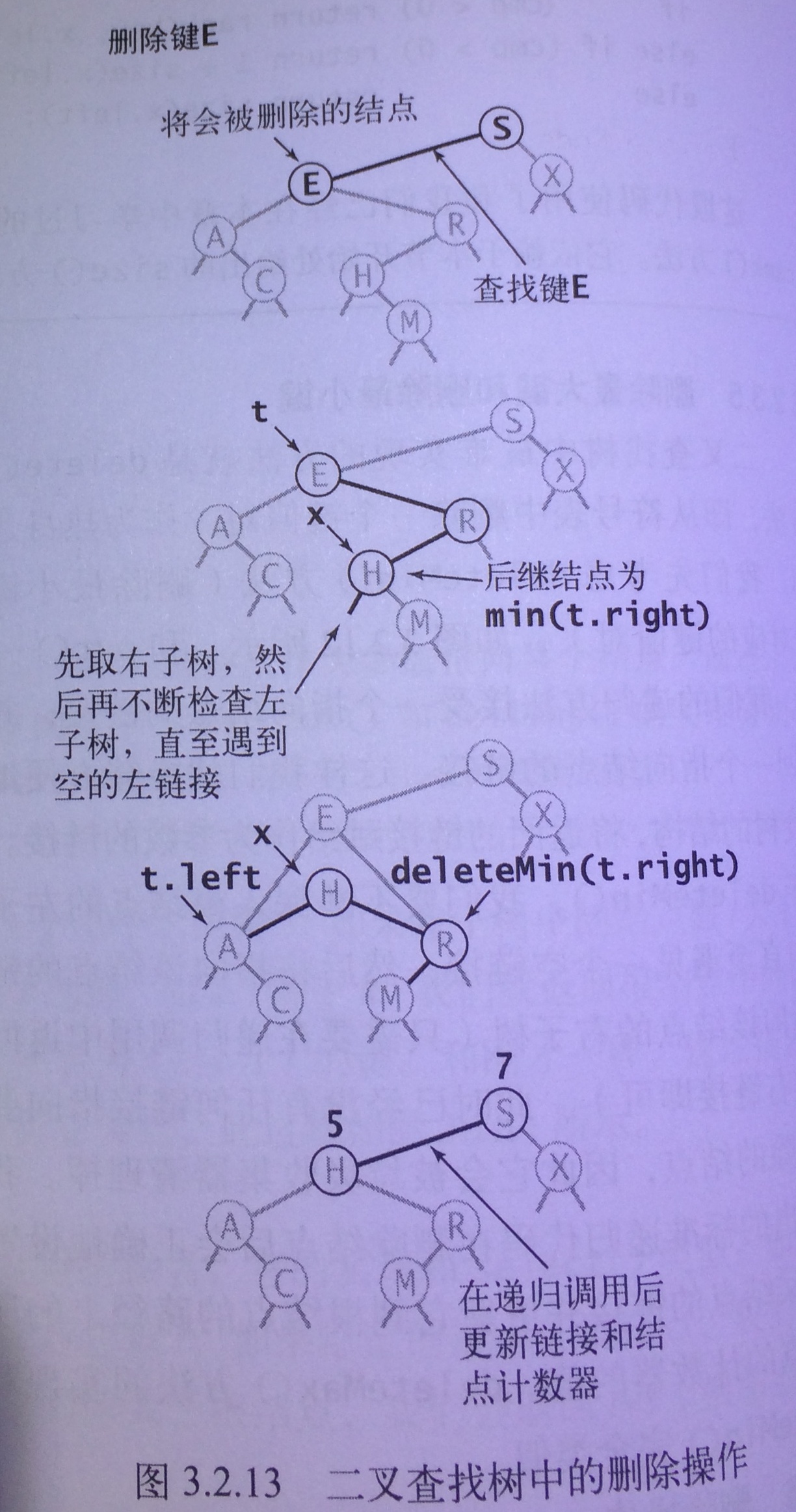
// 这里处理的是上述的第三种情况
Node inherit = min(x.right); // 取得结点x的继承结点
inherit.right = deleteMin(x.right); // 将继承结点从原来位置删除,并重置继承结点右链接
inherit.left = x.left; // 重置继承结点左链接
x = inherit; // 将x替换为继承结点
}
x.N = size(x.left)+ size(x.right) + 1; // 更新结点计数器
return x; // #5
}
public void delete (int key) {
root = delete(key, root);
}

rank方法



public int rank (Node x,int key) {
if(x == null) return 0;
if(key<x.key) {
return rank(x.left,key);
}else if(key>x.key) {
return size(x.left) + 1 + rank(x.right, key);
}else {
return size(x.left);
}
}
public int rank (int key) {
return rank(root,key);
}
select方法
private Node select (Node x,int k) {
if(x==null) return null;
int t = size(x.left);
if(t>k){
return select(x.left,k);
}else if(t<k) {
return select(x.right,k-t-1);
}else {
return x;
}
}
public int select (int k) {
return select(root,k).key;
}
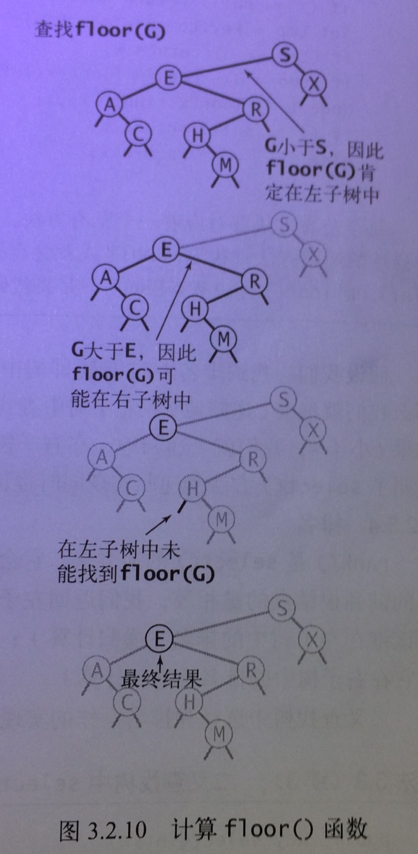
floor、ceiling方法
- 如果递归返回null,说明右子树没有floor值,所以floor值就是当前结点的键,
- 如果递归不为null,说明右子树还有比当前结点键更大的floor值,所以返回递归后的非null的floor值
private Node floor (Node x,int key) {
if(x==null) return null;
if(key<x.key){ // key小于当前结点的键
return floor(x.left,key); // key的floor值在左子树,向左递归
}else if(key==x.key) {
return x; // 和key相等,也是floor值,返回
}else { // 这里排除floor值在左子树,剩下两种可能:floor值是当前结点或在右子树
Node n = floor(x.right, key);
if(n==null) return x; // 右子树没有找到floor值,所以当前结点键就是floor
else return n; // 右子树找到floor值,返回找到的floor值
}
}
public int floor (int key) {
if(root==null) return -1; //树为空, 没有floor值
return floor(root, key).key;
}

【算法】二叉查找树(BST)实现字典API的更多相关文章
- 【算法】二叉查找树实现字典API
参考资料 <算法(java)> — — Robert Sedgewick, Kevin Wayne <数据结构> ...
- 【算法】实现字典API:有序数组和无序链表
参考资料 <算法(java)> — — Robert Sedgewick, Kevin Wayne <数据结构> ...
- 查找系列合集-二叉查找树BST
一. 二叉树 1. 什么是二叉树? 在计算机科学中,二叉树是每个结点最多有两个子树的树结构. 通常子树被称作“左子树”(left subtree)和“右子树”(right subtree). 二叉树常 ...
- 二叉查找树BST 模板
二叉查找树BST 就是二叉搜索树 二叉排序树. 就是满足 左儿子<父节点<右儿子 的一颗树,插入和查询复杂度最好情况都是logN的,写起来很简单. 根据BST的性质可以很好的解决这些东 ...
- 数据结构和算法(Golang实现)(27)查找算法-二叉查找树
二叉查找树 二叉查找树,又叫二叉排序树,二叉搜索树,是一种有特定规则的二叉树,定义如下: 它是一颗二叉树,或者是空树. 左子树所有节点的值都小于它的根节点,右子树所有节点的值都大于它的根节点. 左右子 ...
- 二叉查找树(BST)
二叉查找树(BST):使用中序遍历可以得到一个有序的序列
- [学习笔记] 二叉查找树/BST
平衡树前传之BST 二叉查找树(\(BST\)),是一个类似于堆的数据结构, 并且,它也是平衡树的基础. 因此,让我们来了解一下二叉查找树吧. (其实本篇是作为放在平衡树前的前置知识的,但为了避免重复 ...
- 从一段简单算法题来谈二叉查找树(BST)的基础算法
先给出一道很简单,喜闻乐见的二叉树算法题: 给出一个二叉查找树和一个目标值,如果其中有两个元素的和等于目标值则返回真,否则返回假. 例如: Input: 5 / \ 3 6 / \ \ 2 4 7 T ...
- 【查找结构 2】二叉查找树 [BST]
当所有的静态查找结构添加和删除一个数据的时候,整个结构都需要重建.这对于常常需要在查找过程中动态改变数据而言,是灾难性的.因此人们就必须去寻找高效的动态查找结构,我们在这讨论一个非常常用的动态查找树— ...
随机推荐
- IDEA导入Eclipse项目
目录 一.导入项目 二.启动项目 一.导入项目 1.欢迎界面,选择Import Project 2.选择源码的位置,点击OK 3.选择Eclipse模型,点击Next 4.默认选择,点击Next 5. ...
- Android开发中常见的设计模式(四)——策略模式
策略模式定义了一些列的算法,并将每一个算法封装起来,而且使它们还可以相互替换.策略模式让算法独立于使用它的客户而独立变换. 假设我们要出去旅游,而去旅游出行的方式有很多,有步行,有坐火车,有坐飞机等等 ...
- python——数字问题之_ 变量
在交互模式中,最后被输出的表达式结果被赋值给变量 _ ._ 变量应被用户视为只读变量 >>> a=12/2.3 >>> b=1.2 >>> a*b ...
- css学习2
1.垂直居中 -父元素高度确定的单行文本: 设置父元素的 height 和 line-height 高度一致来实现的.(height: 该元素的高度:line-height: 行高(行间距),指在文 ...
- 安装jdk1.9后报 Error:java: 无效的源发行版: 1.9
现象: intillj IDE 运行main方法 Information:javac 1.8.0_101 was used to compile java sources Error:java: 无效 ...
- 深度学习原理与框架-Tensorflow卷积神经网络-cifar10图片分类(代码) 1.tf.nn.lrn(局部响应归一化操作) 2.random.sample(在列表中随机选值) 3.tf.one_hot(对标签进行one_hot编码)
1.tf.nn.lrn(pool_h1, 4, bias=1.0, alpha=0.001/9.0, beta=0.75) # 局部响应归一化,使用相同位置的前后的filter进行响应归一化操作 参数 ...
- nginx测试小结
最近在工作当中需要使用nginx,就对nginx进行进一步的了解,测试. 工作需求是在微服务架构的基础上,客户端通过nginx反向代理访问服务端,确保当一个服务端出现问题时能及时切换到正 ...
- Java学习笔记(二十二):打包程序
加入一个程序测试完毕,我们就可以将它打包,就可以放到服务器上运行了 找到左下角的终端 点击 输入命令: mvnw clean package -DskipTests=true clean:清除以前生成 ...
- Failed to resolve:com.android.support:appcompat-v7:报错处理
既然是版本问题,那就的先去了解自己的电脑安装的SDK工具版本,点开SDK Manager图标,然后选中Updates就可以看到了 这里我的 sdk 工具版本就是26.1.1了 报错是因为自己的andr ...
- FortiGate外网IPSec链路及运维专线链路到个别网段不通
1.现状: 如图,用户网段有192.168.50.0/24.192.168.51.0/24和192.168.52.0/24.192.168.53.0/24.在防火墙上有静态路由到运维专线的10.160 ...
