GCD on Blackboard

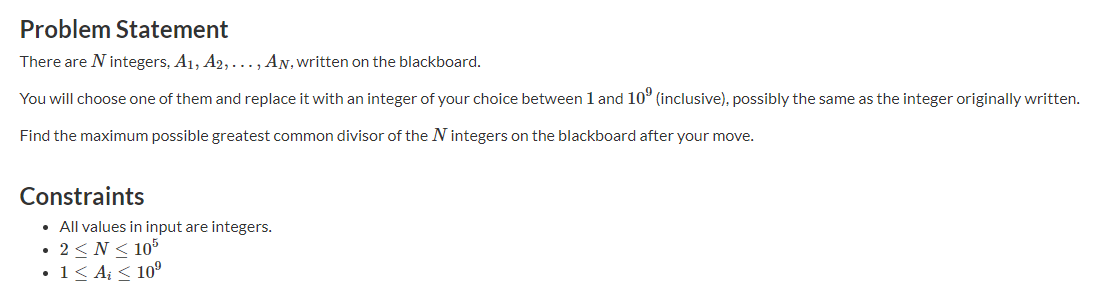
题目大意：给你n个数，然后在这n个数中选一个数，选中的这个数可以变成任意的数，使这n个数的gcd（最大公约数）最大。打印这个最大的gcd。

思路：这题一看貌似很复杂，其实这题只要你知道前缀和  和  后缀和的概念，这题就变得非常简单，用前缀和求出前几个的gcd，后缀和求出后几个的gcd，然后再利用前缀和  和  后缀和求出这个最大的gcd 中间空一个数，即可得到答案。注意：你还要看选中的这个数是第一个还是最后一个，需要比较这个这个的gcd 谁大，就是忘了导致wa了几发。

下面是我写的代码，不喜勿喷。

 #include <iostream>
 #include <cstdio>
 #include <cmath>
 #include <queue>
 #include <map>
 #include <cstring>
 #include <string>
 #include <set>
 #include <vector>
 #include <list>
 #include <deque>
 #include <algorithm>
 #include <stack>
 #include <numeric>
 #include <time.h>
 #include<iomanip>
 #include<sstream>
 #pragma disable:4996)
 using namespace std;
 const long long inf = 0x7f7f7f7f;
 long long GCD(long long a, long long b) { return  == b ? a : GCD(b, a%b); }
 const long long mod = 1e9 + ;
 const double pi = acos(-);
 long long a[];
 long long l[];
 long long r[];
 int main()
 {
     ios_base::sync_with_stdio(false);
     int n;
     cin >> n;
     for (int i = ; i < n; i++)
         cin >> a[i];
     l[] = a[];
     for (int i = ; i < n; i++)
         l[i] = GCD(l[i - ], a[i]);
     r[n - ] = a[n - ];
     for (int i = n - ; i >= ; i--)
         r[i] = GCD(r[i + ], a[i]);
     long long ans = ;
     for (int i = ; i < n-; i++)
         ans = max(GCD(l[i - ], r[i + ]), ans);
     cout << max(ans,max(r[],l[n-])) << endl;
 }