算法实践--不相交集合(Disjoint Sets)

什么是不相交集合(Disjoint Sets)

是这样的一组set，任何元素最多只能在一个set中

至少支持查找Find和合并Union操作

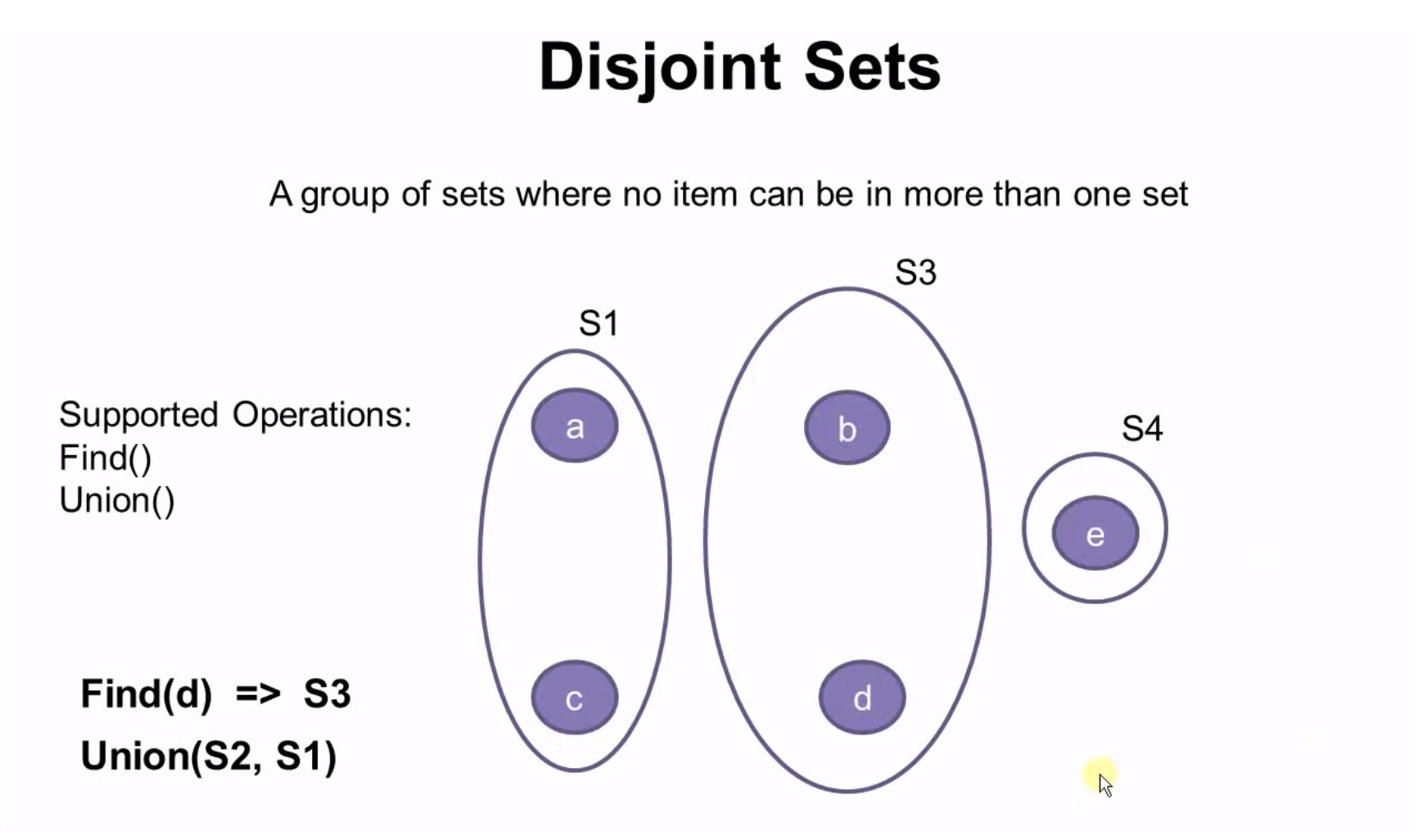
实现方式(基于树)

• 每个set都是一棵树
• 每棵树都由树的根节点识别

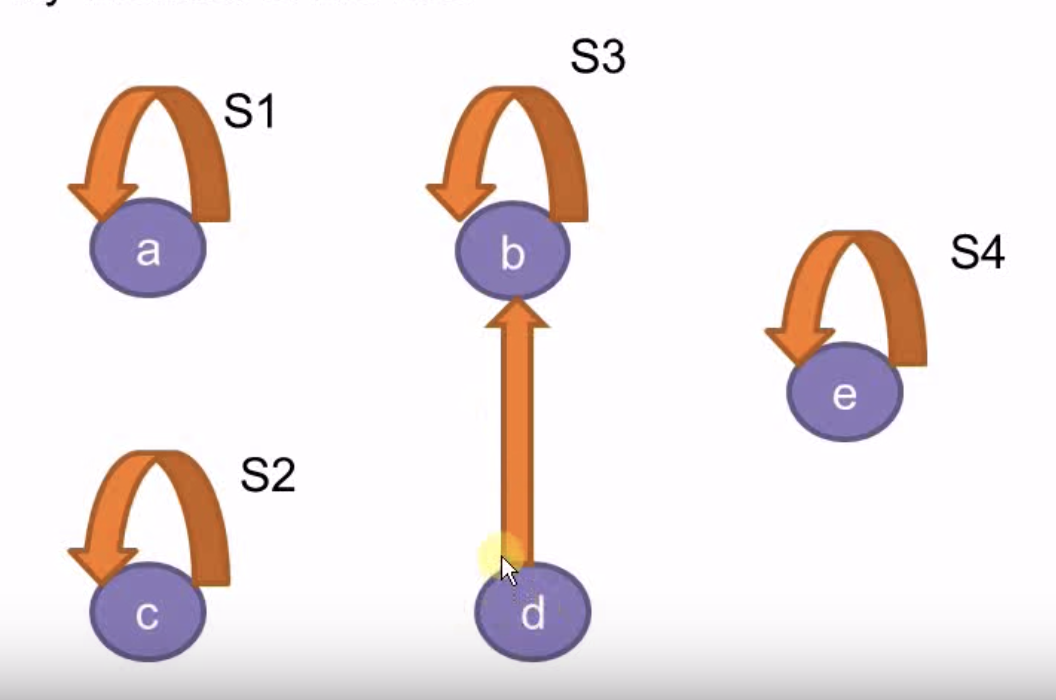
• 合并操作只需要修改根节点的指针

• 合并的复杂度是O(1)
• 查找的复杂度是O(depth) ，树的深度
• 可以方便地通过指针来实现

struct item {
　　char data;
　　Item* parent;
}

• 但是如果数据结构中没有指针，需要自己在外面再套一层结果，比较麻烦
• 还有另一种方法是通过hash表来实现，不需要指针

C++代码实现

class Disjoint_set {
  unordered_map<char, char> PARENT;
  unordered_map<char, int> RANK;  //记录深度
  public:
  Disjoint_set() {
    char universe[] ] {'a', 'b', 'c', 'd', 'e'};
    for (char x : universe) {
      PARENT[x] = x;
      RANK[x] = ;
    }
    PARENT['d'] = 'b';  //d指向b，b和d在同一个集合
    RANK['b']++;
  }

  char Find(char item) {
    if (PARENT[item] == item)
      return item;
    else
      Find(PARENT[item]);
  }

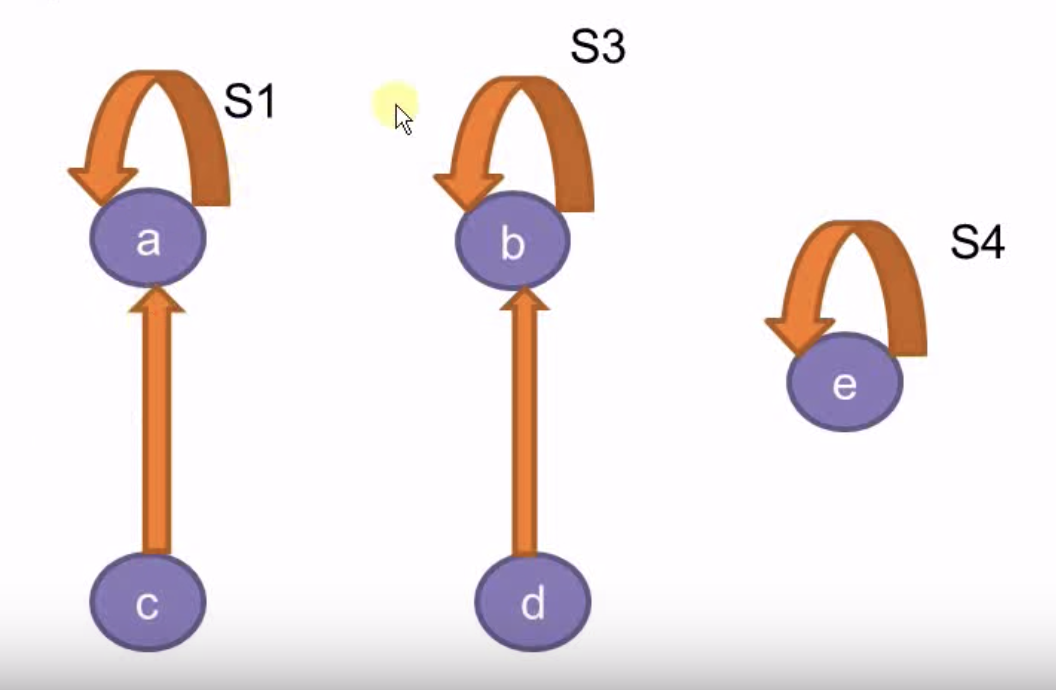
  // 查找的复杂度取决于树的深度，优化合并操作
  void Union(char set_1, char set_2) {  //谁深指向谁
    if (RANK[set_1] > RANK[set_2])
      PARENT[set_2] = set_1;
    else if (RANK[set_2] > RANK[set_1])
      PARENT[set_1] = set_2;
    else {
      PARENT[set_1] = set_2;
      RANK[set_2]++;
    }
  }
};

int main() {
  Disjoint_set ds;
  ds.Find('c'); //返回c
  ds.union('c', 'a'); //c指向a
  ds.Find('c');|//返回a
  ds.union('a', 'b');|//a指向b
}