LeetCode:Climbing Stairs(编程之美2.9-斐波那契数列)

题目链接

You are climbing a stair case. It takes n steps to reach to the top.

Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?

---

算法1：分析：dp[i]为爬到第i个台阶需要的步数，那么dp[i] = dp[i-1] + dp[i-2], 很容易看出来这是斐波那契数列的公式                                        本文地址

class Solution {
public:
    int climbStairs(int n) {
        int fbn1 = 0, fbn2 = 1;
        for(int i = 1; i <= n; i++)
        {
            int tmp = fbn1 + fbn2;
            fbn1 = fbn2;
            fbn2 = tmp;
        }
        return fbn2;
    }
};

算法2：还可以根据斐波那契数列的通项公式来求，对于斐波那契数列 1 1 2 3 5 8 13 21，通项公式如下，这个方法有个缺陷是：使用了浮点数，但是浮点数精度有限， oj中n应该不大，所以可以通过（当 N>93 时 第N个数的值超过64位无符号整数可表示的范围）

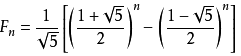
具体推导请参考百度百科

class Solution {
public:
    int climbStairs(int n) {
        //根据斐波那契数列的通项公式
        double a = 1/sqrt(5);
        double b = (1 + sqrt(5)) / 2;
        double c = (1 - sqrt(5)) / 2;
        return (int)round(a * (pow(b, n+1) - pow(c, n+1)));
    }
};

算法3：”编程之美2.9-斐波那契数列“ 中提到了一种logn的算法（实际上利用了幂运算的logn算法），在n比较大时，会高效很多。首先给出本题代码，然后直接截图书上的描述。如果n较大，就需要编写大整数类了

     struct matrix22
     {
         int v11,v12,v21,v22;
         matrix22(int a,int b,int c,int d)
         {
             v11 = a; v12 = b; v21 = c; v22 = d;
         }
         matrix22(){}
     };
     matrix22 matMult(const matrix22 &a, const matrix22 &b)//矩阵乘法
     {
         matrix22 res;
         res.v11 = a.v11*b.v11 + a.v12*b.v21;
         res.v12 = a.v11*b.v12 + a.v12*b.v22;
         res.v21 = a.v21*b.v11 + a.v22*b.v21;
         res.v22 = a.v21*b.v12 + a.v22*b.v22;
         return res;
     }
     matrix22 matPow(const matrix22 &a, int exp)//矩阵求幂
     {
         matrix22 res(,,,);//初始化结果为单位矩阵
         matrix22 tmp = a;
         for(; exp; exp >>= )
         {
             if(exp & )
                 res = matMult(res, tmp);
             tmp = matMult(tmp, tmp);
         }
         return res;
     }
 
 class Solution {
 public:
     int climbStairs(int n) {
         matrix22 A(,,,);
         A = matPow(A, n-);
         return A.v11 + A.v21;
     }
 };

【版权声明】转载请注明出处：http://www.cnblogs.com/TenosDoIt/p/3465356.html