EZ 2017 12 30 2018noip第二次膜你赛

　　去年的比赛了，然而今天才改好。

　　总体难度适中，有大佬AK。

　　主要是自己SB第二题没想出来，然后又是可怜的100来分。

　　T1 一道二分+数学的题目。

　　我们可以二分叫的次数，然后用公式（等差数列，公差都是zi）算一个最大的可行的数目。

　　最后把多余的加上去即可。

　　注意当xi，yi都等于0的情况。

　　CODE

#include<cstdio>
#include<cmath>
using namespace std;
typedef long long LL;
LL ans,n,t,t_2,t_s,x,y,z,res,l,r,mid,temp;
inline void read(LL &x)
{
    x=; char ch=getchar();
    while (ch<''||ch>'') ch=getchar();
    while (ch>=''&&ch<='') x=x*+ch-'',ch=getchar();
}
int main()
{
    freopen("brute.in","r",stdin); freopen("brute.out","w",stdout);
    read(n); read(t); t_2=t*;
    while (n--)
    {
        read(x); read(y); read(z);
        l=; if (x+y) r=t/(x+y); else r=(LL)sqrt(t_2/z)+;
        temp=*x+*y;
        while (l<=r)
        {
            mid=l+r>>;
            if (mid*(temp+mid*z-z)<=t_2) res=mid,l=mid+; else r=mid-;
        }
        ans+=res*(*y+z*res-z)/;
        t_s=t-res*(temp+res*z-z)/-x;
        if (t_s>) ans+=t_s;
    }
    printf("%lld",ans);
    return ;
}

　　T2 标算用了神奇的。。。数据结构来打。

　　然而当时A了这道题的都是用超级简单的方法水过的。

　　现在只讨论玄学算法（即超级水过的算法）。

　　由于题目不要求分别输出每一次的值，所以我们只需要先把全部操作做完，最后1次DFS遍历一下每个点一共访问了几次。

　　第1次操作ans+1； 第2次 ans+2； 第3次 ans+3;  第n次 ans+n；

　　然后又是玄学的等差数列求和即可。ans+=（n+1)*n/2；

　　CODE

#include<cstdio>
#include<vector>
using namespace std;
typedef long long LL;
const int N=;
vector <LL> a[N];
LL n,m,i,x,ans,t[N],f[N];
struct io
{
    char op[ << ] , * s;
    io()
    {
        freopen( "chiye.in" , "r" , stdin );
        freopen( "chiye.out" , "w" , stdout );
        fread( s = op ,  ,  <<  , stdin );
    }
    inline void read(LL &u)
    {
        u = ;
        while( * s <  ) s++;
        while( * s >  )
            u = u *  + * s++ - ;
    }
} ip;
#define read ip.read
inline void dfs(int k)
{
    f[k]+=t[k];
    for (int i=;i<a[k].size();++i)
    f[k]+=t[a[k][i]],f[a[k][i]]+=t[k],dfs(a[k][i]);
}
int main()
{
    read(n); read(m);
    for (i=;i<=n;++i)
    {
        read(x);
        a[x].push_back(i);
    }
    while (m--)
    {
        read(x);
        t[x]++;
    }
    dfs();
    for (i=;i<=n;++i)
    ans+=f[i]*(f[i]+)/;
    printf("%lld",ans);
    return ;
}

　　（fread模板是免费提供的）

　　T3 Tarjan缩点+树形DP

　　就这道题改了很久，到现在还是因为不会Tarjan缩点（打了DFS）TLE了4个点。

　　首先前30分想怎么暴力怎么暴力。

　　然后发现因为这个图只有简单环，所以左右的点可以分成2种：圆点和方点。

　　简单地说，圆点就是原来的图中不包括在任何一个环中的点；方点就是把一个简单环缩成的一个点。如下图：

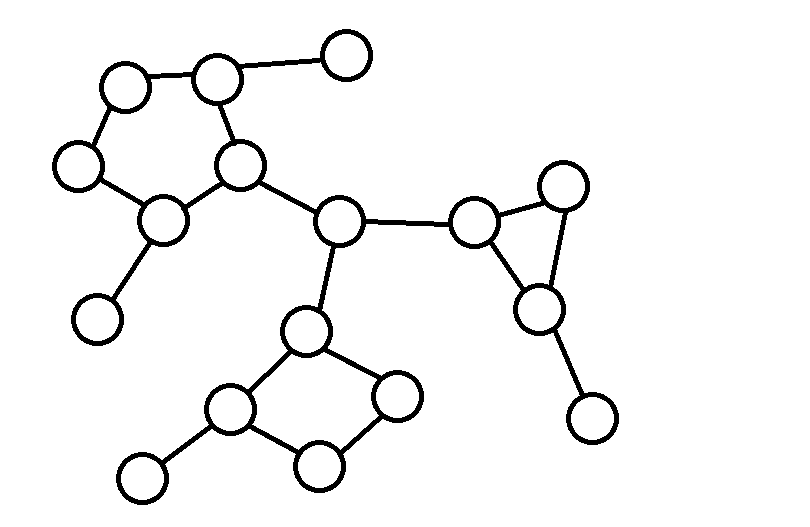
变成

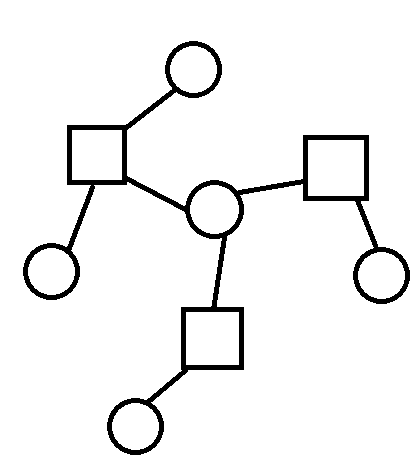
　　然后我们发现一个眼镜的两边都是方点，如果两个端点确定，那么这两个点可以组成的眼镜数量就是2^（两个端点之间的方点个数）；

　　接下来又有50——70分可以暴力DFS了。

　　如果想得满分，就得考虑树形DP，设f[x]为以x为根的子树（包括x）一共有多少“一半的眼镜”（即只有一个端点的）

　　然后状态转移 ：

　　f[x] = Σ( f[ son[x] ] );

　　如果x是圆点，则f[x]不变

　　如果x是方点，则f[x] = f[x] * 2 + 1（可以走两次再加上它自己）

　　每次做的时候更新ans即可。具体看代码。

　　CODE

#include<cstdio>
#include<vector>
#include<cstring>
using namespace std;
const int N=,mod=;
vector <int> a[N],b[N];
int n,m,f[N],num[N],pre[N],i,j,tot,x,y;
bool kinds[N],vis[N],use[N];
long long ans;
inline void read(int &x)
{
    x=; char ch=getchar();
    while (ch<''||ch>'') ch=getchar();
    while (ch>=''&&ch<='') x=x*+ch-'',ch=getchar();
}
inline void print(int k)
{
    if (pre[k]) print(pre[k]);
    num[k]=tot;
    use[k]=;
}
inline void find(int s,int k)
{
    for (int i=;i<a[k].size();++i)
    if ((!vis[a[k][i]])&&(!use[a[k][i]])) pre[a[k][i]]=k,vis[a[k][i]]=,find(s,a[k][i]),vis[a[k][i]]=; else
    if (a[k][i]==s&&a[k][i]!=pre[k])
    {
        print(k);
        kinds[tot]=;
        return;
    }
}
inline int dp(int k)
{
    vis[k]=;
    for (int i=;i<b[k].size();++i)
    {
        int now=b[k][i];
        if (vis[now]) continue;
        int temp=dp(b[k][i]);
        ans=(ans+f[k]*(kinds[k]?2ll:1ll)*temp)%mod;
        f[k]=(f[k]+temp)%mod;
    }
    if (kinds[k]) ans=(ans+f[k])%mod,f[k]=(f[k]*+)%mod;
    return f[k];
}
int main()
{
    freopen("dark.in","r",stdin); freopen("dark.out","w",stdout);
    read(n); read(m);
    for (i=;i<=m;++i)
    {
        read(x); read(y);
        a[x].push_back(y); a[y].push_back(x);
    }
    for (i=;i<=n;++i)
    if (!use[i]) ++tot,num[i]=tot,use[i]=,kinds[tot]=,memset(pre,,sizeof(pre)),vis[i]=,find(i,i),vis[i]=;
    for (i=;i<=n;++i)
    for (j=;j<a[i].size();++j)
    if (num[i]!=num[a[i][j]]) b[num[i]].push_back(num[a[i][j]]);
    dp();
    printf("%lld",ans);
    return ;
}