N皇后问题 各种优化

0.问题引入

N皇后问题是一个经典的问题，在一个N*N的棋盘上放置N个皇后，每行一个并使其不能互相攻击（同一行、同一列、同一斜线上的皇后都会自动攻击），问有多少种摆法。

题目链接：https://www.luogu.org/problemnew/show/P1219

1、普通回溯

回溯算法也叫试探法，它是一种系统地搜索问题的解的方法。回溯算法的基本思想是：从一条路往前走，能进则进，不能进则退回来，换一条路再试。

算法思想：

1. 在第k（1≤k≤N）行选择一个位置，判断这个位置是否可以摆，可以摆就进入第 k+1 行，不可以就试下一个位置；

2. 如果一直试到本行最后一个都不行，说明前面k-1行有位置选得不恰当，回到第 k-1 行，试 k-1 行的下一个位置。

3. 反复执行1,2，到最后一行摆上棋子时，说明找到了一个解。

一个问题能用回溯法求解，它的解具有$N$元组的形式，我们使用用$N$元组$(x_1,x_2,...,x_n)$表示问题的解，其中$x_i$表示第$i$行的皇后所处的列号。

核心代码：

//row,col表示当前尝试摆放皇后的行号与列好
bool check(int row, int col) {
    for (int i = ; i < row; i++) {
        if (x[i] == col)//列冲突
            return false;
        if (abs(row - i) == abs(col - x[i]))//对角线冲突
            return false;
    }
    return true;
}
void DFS(int k) {
    if (k == N + ) {
        //获得了一个解
        cnt++;
        return;
    }
    for (int i = ; i <= N; i++) {
        if (check(k, i)) {
            x[k] = i;//标注第k行上第i个位置摆上了皇后
            DFS(k + );
        }
    }
}

1.1 递归实现：

N=11,12的时就顶不住了，嗝屁了。

#include <iostream>
#include <math.h>
using namespace std;
 
int x[];
int N, cnt;
 
bool check(int row, int col) {
    //回溯，不会受到后面行的影响
    for (int i = ; i < row; i++) {
        if (x[i] == col)return false;
        if (abs(row - i) == abs(col - x[i]))return false;
    }
    return true;
}
void DFS(int k) {
    if (k == N + ) {
        cnt++;
        if (cnt <= ) {
            for (int i = ; i <= N; i++) {
                cout << x[i] << " ";
            }
            cout << endl;
        }
        return;
    }
    for (int i = ; i <= N; i++) {
        if (check(k, i)) {
            x[k] = i;
            DFS(k + );
        }
    }
}
 
int main() {
    cin >> N;
    DFS();
    cout << cnt << endl;
    return ;
}

1.2 非递归实现：

算法优化一般不从这里考虑，因为非递归虽然是会快一点，但也只是那么一点而已，数据量小几乎没有区别，两个都跑不过去。

#include <iostream>
#include <math.h>
using namespace std;
 
int x[];
int N, cnt;
 
bool check(int row, int col) {
    //回溯，不会受到后面行的影响
    for (int i = ; i < row; i++) {
        if (x[i] == col)return false;
        if (abs(row - i) == abs(col - x[i]))return false;
    }
    return true;
}
 
void queen(){
    //i表示第几册，j表示在第i层搜索位置
    int i = , j = ;
    while (i <= N){
        while (j <= N){
            //如果当前位置合法
            if (check(i, j)) {
                //把x[i]暂时赋值成j
                x[i] = j;
                j = ;
                break;
            }
            else
                j++;
        }
        //第i行没有找到可以放置皇后的位置
        if (x[i] == ){
            //如果回溯到了第0行，说明完成了
            if (i == )
                break;
            //回溯
            else{
                i--;
                j = x[i] + ;//j为上一行的皇后位置+1
                x[i] = ;//上一行清零
                continue;
            }
        }
        //如果找到了第N层，输出出来
        if (i == N){
            cnt++;
            if (cnt <= ) {
                for (int i = ; i <= N; i++) {
                    cout << x[i] << " ";
                }
                cout << endl;
            }
            j = x[i] + ;
            x[i] = ;
            continue;
        }
        i++;
    }
}
int main() {
    cin >> N;
    //DFS(1);
    queen();
    cout << cnt << endl;
    return ;
}

2、减半优化

其实仔细看解就不难发现，每个结果总有另一个与之对称。我们可以利用棋盘的对称, 只用回溯一半 。效率能提升50%。

对于第一层，只下该行的前一半的位置即可。但是对于奇数的N，计算出来的结果会将第一行下在中间位置的解算了两遍。所以要单独处理一下。

效率提升不到50%（奇数的情况），并不算多，题目的测试数据只到13，勉强跑过了，但优化还没结束。

#include <iostream>
#include <vector>
#include <math.h>
using namespace std;
 
int x[];
vector<int> v[];
int N, cnt;
int flag, oddCnt;
 
bool check(int row, int col) {
    //回溯，不会受到后面行的影响
    for (int i = ; i < row; i++) {
        if (x[i] == col)return false;
        if (abs(row - i) == abs(col - x[i]))return false;
    }
    return true;
}
void DFS(int k) {
    if (k == N + ) {
        if (flag&&x[] == (N + ) / ) {
            oddCnt++;
            if (oddCnt %  == )cnt++;
        }
        else
        cnt++;
        if (cnt <= ) {
            for (int i = ; i <= N; i++) {
                cout << x[i] << " ";
                v[cnt - ].push_back(x[i]);
            }
            cout << endl;
        }
        return;
    }
    int len = (k == ) ? (N + flag) /  : N;
    for (int i = ; i <= len; i++) {
        if (check(k, i)) {
            x[k] = i;
            DFS(k + );
        }
    }
}
 
int main() {
    cin >> N;
    if (N & )flag = ;
    DFS();
    for (int i = cnt, j = cnt - ; i <  && j >= ; i++, j--) {
            for (int k = N - ; k >= ; k--) {
                cout << v[j][k] << " ";
            }
            cout << endl;
        }
 
    cout << cnt* << endl;
    return ;
}

3、优化判断

以本图为例：

每条橙色对角线的行列之差是相同的。

每条蓝色对角线的行列之和是相同的。

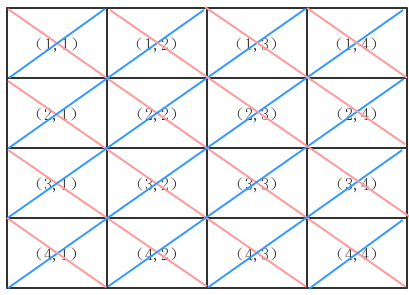
用两个bool数组用来记录行列之和为 i 的正斜线、行列之差为 i 的反斜线是否已经被占据。考虑到行列之差可能为负数，棋盘坐标 [x,y] 对应下标 [ x - y + n ]。

再用一个数组记录第 i 列是否有元素。

#include <iostream>
using namespace std;
 
int N, cnt,a[];
//正对角线、副对角线、行
bool x1[], x2[], y[];
 
void DFS(int k) {
    if (k == N + ) {
        cnt++;
        if (cnt <= ) {
            for (int i = ; i <= N; i++) {
                cout << a[i] << " ";
            }
            cout << endl;
        }
        return;
    }
    for (int i = ; i <= N; i++) {
        //这里x2下标不能用abs，那样是不对的
        if (!x1[i + k] && !x2[k - i + N] && !y[i]) {
            a[k] = i;
            x1[i + k] = ;
            x2[k - i + N] = ;
            y[i] = ;
            DFS(k + );
            x1[i + k] = ;
            x2[k - i + N] = ;
            y[i] = ;
        }
    }
}
 
int main() {
    cin >> N;
    DFS();
    cout << cnt << endl;
    return ;
}

当N较大时，算法会耗费大量的次数在无用的回溯上，时间还是没有显著提高。

4、位运算优化

警告:以下代码可能引起不适，请60岁以下用户在家长陪同下阅读。

位运算是计算机最快的操作，我们可以用数的二进制位表示各纵列、对角线是否可以放置皇后。

看讲解的：https://blog.csdn.net/Hackbuteer1/article/details/6657109 博主讲的很清楚了。

#include <iostream>
#include <queue>
using namespace std;
 
int n, limit, cnt;
int x[], k = ;
//行，左对角线，右对角线
void DFS(int row,int left,int right) {
    if (row != limit) {
        //row|left|right表示这一行的所有禁止位置，取反再和limit按位与，得到的是该行可以放的几个位置
        int pos = limit & ~(row | left | right);
        //每一个可以摆的位置，都要做一次
        while (pos) {
            //找到的可以放皇后的位置（pos二进制最右边的一个1）
            int p = pos & -pos;// pos & (~pos+1);
            //把这一位置0，表示不为空
            pos &= pos - ;//pos=pos-p;
            //把p所在row，left，right的位都置1。
            //(left | p)<< 1 是因为这一行由左对角线造成的禁止位在下一行要右移一下；right同理
            DFS(row | p, (left | p) << , (right | p) >> );
        }
    }
    else {
        cnt++;
    }
}
 
int main() {
    cin >> n;
    limit = ( << n) - ;
    DFS(, , );
    cout << cnt << endl;
    return ;
}

#include <iostream>
#include <queue>
using namespace std;
 
int n, limit, cnt;
int x[], k = ;
//行，左对角线，右对角线
void DFS(int row,int left,int right) {
    if (row != limit) {
        int pos = limit & ~(row | left | right);
        while (pos) {
            //找到的可以放皇后的位置
            int p = pos & -pos;// pos & (~pos+1);
            pos &= pos - ;
            if (cnt < ) {
                int t = p, num = ;
                while (t != ) {
                    num++;
                    t >>= ;
                }
                x[k++] = num;
            }
            DFS(row | p, (left | p) << , (right | p) >> );
            if (cnt < ) k--;
        }
    }
    else {
        if (cnt < ) {
            for (int i = ; i <= n; i++) {
                cout << x[i] << " ";
            }
            cout << endl;
        }
        cnt++;
    }
}
 
int main() {
    cin >> n;
    limit = ( << n) - ;
    DFS(, , );
    cout << cnt << endl;
    return ;
}

果然名不虚传~