TXNLP 09-17

上节课讲了一些算法的复杂度,都比较简单,我就没有单独截图。1 n n^2 nlogn logn。。。等等
其实一些排序问题也比较简单。还是给大家列举一下.
归并排序:

主定理定理。。吐血


算法复杂度相关的知识:函数渐进阶,记号 O、Ω、θ和 o;Master 定理。
先插一句,在算法复杂度分析中,log 通常表示以 2 为底的对数。
算法复杂度(算法复杂性)是用来衡量算法运行所需要的计算机资源(时间、空间)的量。通常我们利用渐进性态来描述算法的复杂度。

比如 T(n) = 2 * n ^ 2 + n log n + 3,那么显然它的渐进性态是 2 * n ^ 2,因为当 n→∞ 时,后两项的增长速度要慢的多,可以忽略掉。引入渐进性态是为了简化算法复杂度的表达式,只考虑其中的主要因素。当比较两个算法复杂度的时候,如果他们的渐进复杂度的阶不相同,那只需要比较彼此的阶(忽略常数系数)就可以了。
总之,分析算法复杂度的时候,并不用严格演算出一个具体的公式,而是只需要分析当问题规模充分大的时候,复杂度在渐进意义下的阶。记号 O、Ω、θ和 o 可以帮助我们了解函数渐进阶的大小。
假设有两个函数 f(n) 和 g(n),都是定义在正整数集上的正函数。上述四个记号的含义分别是:

可见,记号 O 给出了函数 f(n) 在渐进意义下的上界(但不一定是最小的),相反,记号Ω给出的是下界(不一定是最大的)。如果上界与下界相同,表示 f(n) 和 g(n) 在渐进意义下是同阶的(θ),亦即复杂度一样。
列举一些常见的函数之间的渐进阶的关系:

Fibonanci number (斐波那契数)
序列一次为 1,1,2,3,5,8,13,21,.... 问题: 怎么求出序列中第N个数?
T(n) = T(n-2) + T(n-1) def fib(n):
# base case
if n < 3:
return 1
return fib(n-2)+fib(n-1)
print (fib(50))
斐波那契的时间复杂度:
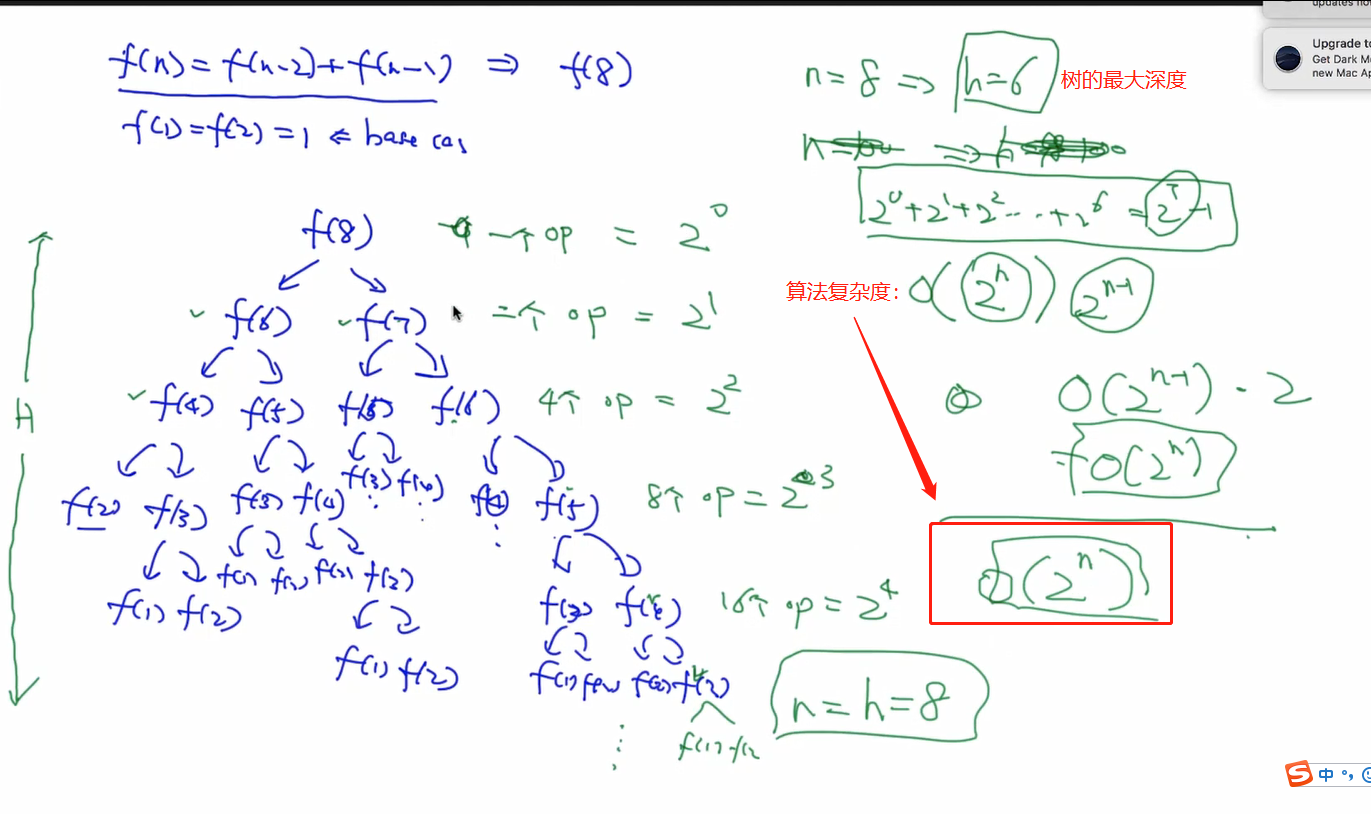
但是会发现计算了很多重复的例如f(3)等等。所以 后面会讲 DP 的算法可以存储中间的数据,不用重复计算。
斐波那契的空间复杂度:

动态规划:

# 时间复杂度?
import numpy as np
def fib(n):
tmp = np.zeros(n)
tmp[0] = 1
tmp[1] = 1
for i in range(2,n):
tmp[i] = tmp[i-2]+tmp[i-1] return tmp[n-1] O(N) O(2^n) def fib(n):
tmp = np.zeros(n)
tmp[0] = 1
tmp[1] = 1
for i in range(2,n):
tmp[i] = tmp[i-2]+tmp[i-1] return tmp[n-1] def fib(n):
a,b=1,1
c =0
for i in range(2,n):
c = a + b
a = b
b = c
return c 思考题: 怎么在O(1)的时间复杂度下计算FIB(N)? 套公式 思考题: 这个公式怎么得来的?
提示: 转换成矩阵的连乘的形式, 矩阵连乘可以简化(MATRIX DECOMPOSION)
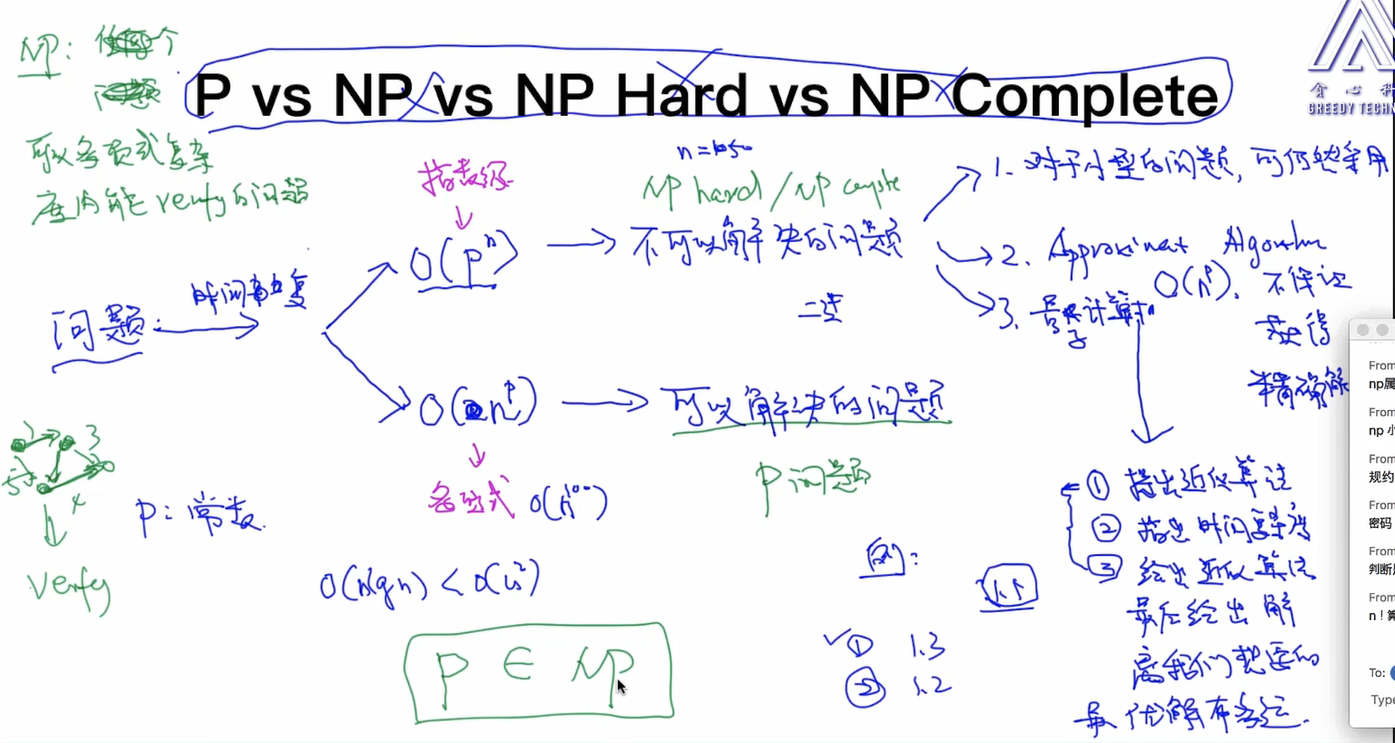
简单介绍一下:
P问题:
一个问题可以在多项式(O(n^k))的时间复杂度内解决。
NP问题:
一个问题的解可以在多项式的时间内被验证。
NP-hard问题:
任意np问题都可以在多项式时间内归约为该问题,但该问题本身不一定是NP问题。归约的意思是为了解决问题A,先将问题A归约为另一个问题B,解决问题B同时也间接解决了问题A。
NPC问题:
既是NP问题,也是NP-hard问题。
时间复杂度并不是表示一个程序解决问题需要花多少时间,而是当问题规模扩大后,程序需要的时间长度增长得有多快。也就是说,对于高速处理数据的计算机来说,处理某一个特定数据的效率不能衡量一个程序的好坏,而应该看当这个数据的规模变大到数百倍后,程序运行时间是否还是一样,或者也跟着慢了数百倍,或者变慢了数万倍。不管数据有多大,程序处理花的时间始终是那么多的,我们就说这个程序很好,具有O(1)的时间复杂度,也称常数级复杂度;数据规模变得有多大,花的时间也跟着变得有多长,这个程序的时间复杂度就是O(n),比如找n个数中的最大值;而像冒泡排序、插入排序等,数据扩大2倍,时间变慢4倍的,属于O(n^2)的复杂度。还有一些穷举类的算法,所需时间长度成几何阶数上涨,这就是O(a^n)的指数级复杂度,甚至O(n!)的阶乘级复杂度。不会存在O(2*n^2)的复杂度,因为前面的那个“2”是系数,根本不会影响到整个程序的时间增长。同样地,O (n^3+n^2)的复杂度也就是O(n^3)的复杂度。因此,我们会说,一个O(0.01*n^3)的程序的效率比O(100*n^2)的效率低,尽管在n很小的时候,前者优于后者,但后者时间随数据规模增长得慢,最终O(n^3)的复杂度将远远超过O(n^2)。我们也说,O(n^100)的复杂度小于O(1.01^n)的复杂度。
容易看出,前面的几类复杂度被分为两种级别,其中后者的复杂度无论如何都远远大于前者:一种是O(1),O(log(n)),O(n^a)等,我们把它叫做多项式级的复杂度,因为它的规模n出现在底数的位置;另一种是O(a^n)和O(n!)型复杂度,它是非多项式级的,其复杂度计算机往往不能承受。当我们在解决一个问题时,我们选择的算法通常都需要是多项式级的复杂度,非多项式级的复杂度需要的时间太多,往往会超时,除非是数据规模非常小。
P类问题的概念:如果一个问题可以找到一个能在多项式的时间里解决它的算法,那么这个问题就属于P问题。
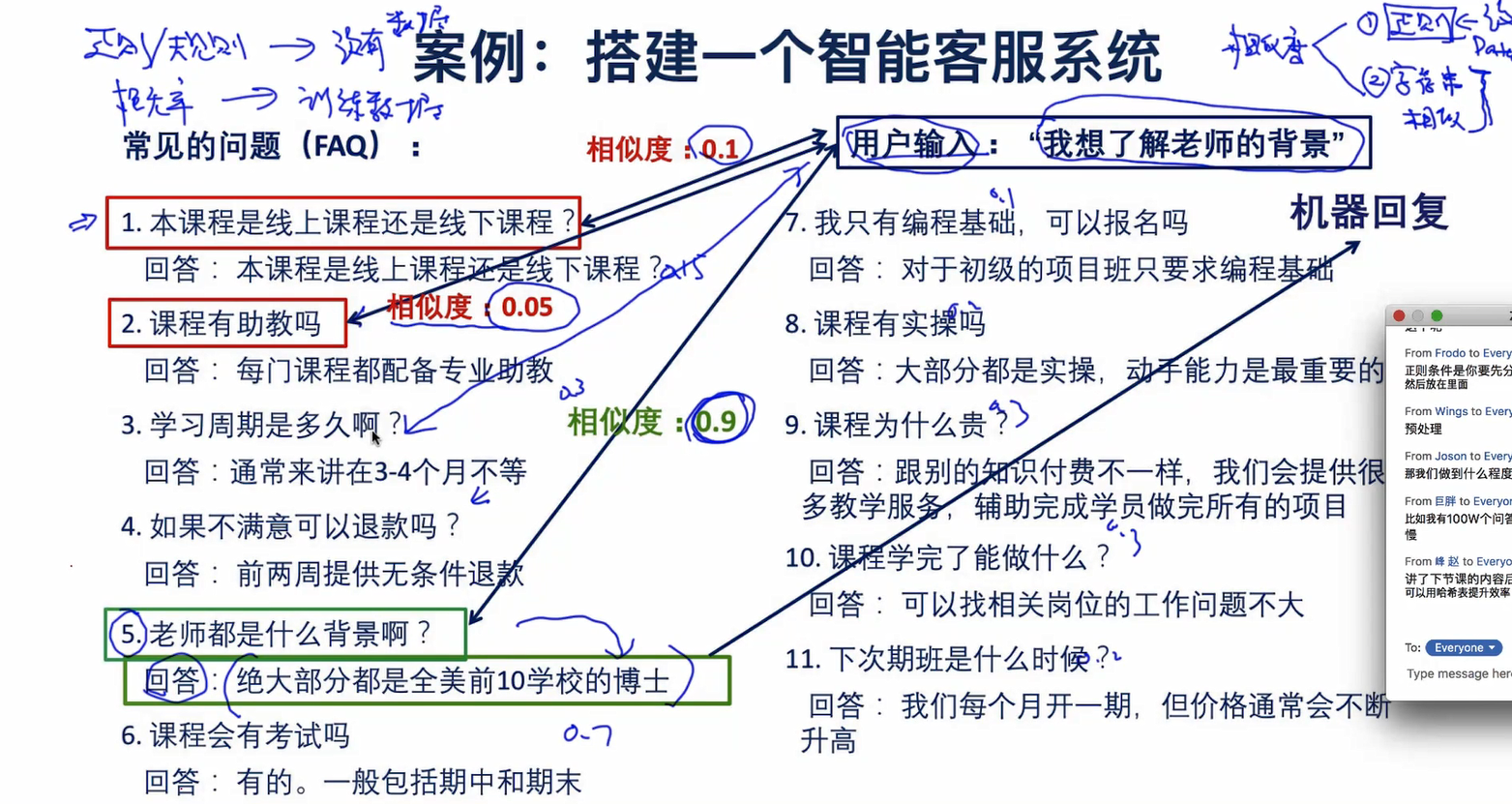
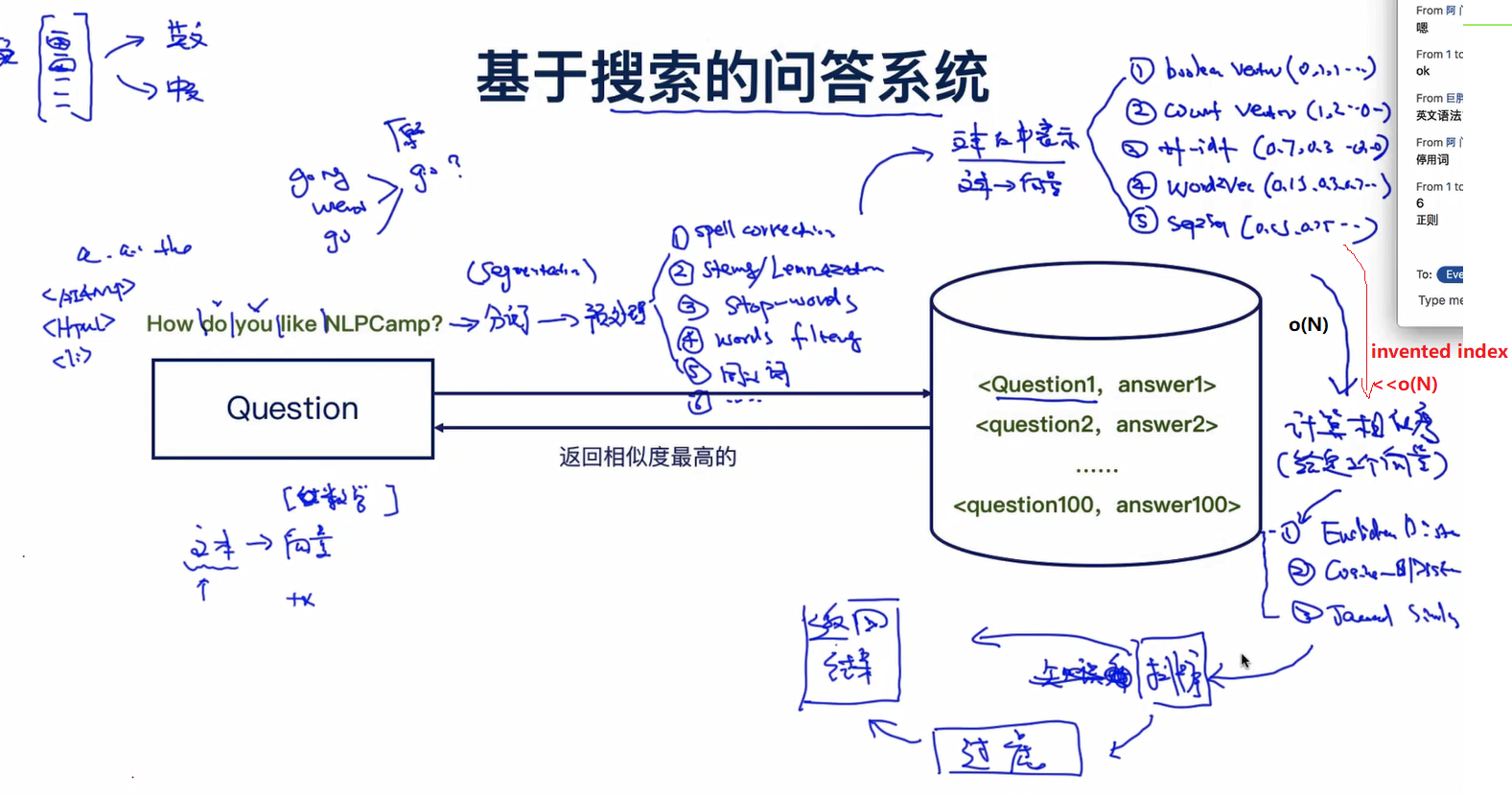
TXNLP 09-17的更多相关文章
- gulp ( http://markpop.github.io/2014/09/17/Gulp入门教程 )
前言 最近流行前端构建工具,苦于之前使用Grunt,代码很难阅读,现在出了Gulp,真是摆脱了痛苦.发现了一篇很好的Gulp英文教程,整理翻译给大家看看. 为什么使用Gulp Gulp基于Node.j ...
- 【.NetRemoting-2】2015.09.17
[Remoting架构] [1]是.NetFramework的一个重要组成 [2]框架的两个重要特性 [A]基本实现[B]可扩展/可定制 [各个组成部分] [1][客户端,客户端应用程序域] [组成] ...
- 2018/09/17《涂抹MySQL》【性能优化及诊断】学习笔记(七)
读 第十三章<MySQL的性能优化与诊断> 总结 一说性能优化,整个人都像被打了鸡血一样
- 2018.09.17 atcoder Tak and Hotels(贪心+分块)
传送门 一道有意思的题. 一开始想错了,以为一直lowerlowerlower_boundboundbound就可以解决询问,结果交上去TLE了之后才发现时间复杂度是错的. 但是贪心思想一定是对的,每 ...
- 2018.09.17 atcoder Tak and Cards(背包)
传送门 背包经典题. 直接f[i][j]f[i][j]f[i][j]表示选i张牌和为j的方案数. 最后统计答案就行了. 代码: #include<bits/stdc++.h> #defin ...
- 2018.09.17 atcoder Digit Sum(数论)
传送门 数论好题啊. 首先对于b<=sqrt(n)b<=sqrt(n)b<=sqrt(n)的情况直接枚举b判断一下就行了. 下面谈一谈如何解决b>sqrt(n)b>sqr ...
- 2018.09.17 bzoj1260: [CQOI2007]涂色paint(区间dp)
传送门 区间dp简单题啊. 很显然用f[l][r]f[l][r]f[l][r]表示把区间[l,r][l,r][l,r]按要求染好的代价. 这样可以O(n)O(n)O(n)枚举断点转移了啊. 显然如果断 ...
- 数字图像处理:基于MATLAB的车牌识别项目 标签: 图像处理matlab算法 2017-06-24 09:17 98人阅读 评论(0)
学过了数字图像处理,就进行一个综合性强的小项目来巩固一下知识吧.前阵子编写调试了一套基于MATLAB的车牌识别的项目的代码.今天又重新改进了一下代码,识别的效果好一点了,也精简了一些代码.这里没有使用 ...
- 作业成绩 final 20161124-1201 09:00
final阶段,20161124-1201 09:00. 申诉截止时间 20161206 12:00,微信联系杨贵福. 凡描述需求或BUG时,应给出以下4项: 你期待看到的现象如何 你实际看到的现象 ...
- JavaSE学习总结第09天_面向对象4
09.01 final关键字引入 例: class Fu { public final void show() { System.out.println("访问底层资源"); ...
随机推荐
- 小记--------sparksql和DataFrame的小小案例java、scala版本
sparksql是spark中的一个模块,主要用于进行结构化数据的处理,他提供的最核心的编程抽象,就是DataFrame.同时,sparksql还可以作为分布式的sql查询引擎. 最最重要的功能就是从 ...
- springboot 论坛项目
项目演示地址:http://www.mawen.co/ 快速搭建sprintboot项目 运行第一个springboot项目 leaf package hello; import org.spring ...
- PHPRedis教程之geo
前言 支持 GEO 系列命令的 Redis 版本从 3.2.0 起开始才可以使用,所以之前版本就不要想了. 函数列表 geoadd - 将指定的地理空间项(纬度,经度,名称)添加到指定的键, 数据作为 ...
- 关于php性能优化
php性能优化 1.尽量静态化: 如果一个方法能被静态,那就声明它为静态的,速度可提高1/4,甚至我测试的时候,这个提高了近三倍. 当然了,这个测试方法需要在十万级以上次执行,效果才明显. 其实静态方 ...
- winform中如何使用确认对话框
在系统中,常需要这样的功能,让用户确认一些信息:如下图: [退出系统]按钮关键代码如下: private void btnExit_Click(object sender, EventArgs e) ...
- SpringBoot 进阶
SpringBoot 进阶 这里讲两个小方面: 表单验证 AOP 1. 表单验证 SpringBoot 中的表单验证功能步骤如下: 在 controller 类中将用 @PathVariable 和 ...
- 题解 P2280 【[HNOI2003]激光炸弹】
题目链接: https://www.luogu.org/problemnew/show/P2280 思路: 简单的二维前缀和,最后扫描一遍求 max(ans,f[i][j]+f[i-r][j-r]-f ...
- centos配置LVS
LVS有三种工作模式:NAT, TUN, DR. DR是三种工作模式中性能最高的,TUN次之. 本文记录LVS/TUN和LVS/DR工作模式的配置过程. 环境: 三台CentOS 7 x64 虚拟机 ...
- spark内存管理详解
Spark 作为一个基于内存的分布式计算引擎,其内存管理模块在整个系统中扮演着非常重要的角色.理解 Spark 内存管理的基本原理,有助于更好地开发 Spark 应用程序和进行性能调优.本文旨在梳理出 ...
- 输出指令(echo指令和printf 命令)
Shell echo命令 Shell 的 echo 指令与 PHP 的 echo 指令类似,都是用于字符串的输出.命令格式: echo string 您可以使用echo实现更复杂的输出格式控制. 1. ...
