realpython教程之机器学习之Windows下的环境配置

不得不说，realPython的教程确实写的仔细，准确，有逻辑。果然高质量的学习材料还是更利于学的。
反观我们学校，似乎就有些急功近利了。连Python语言基础都没学，就直接讲深度学习。完全不符合学习规律——循序渐进。螺旋上升。

入门教程的例子一定要考虑到受众的知识储备。
千万不要期望小白知道那些你习以为常的东西。
如果写得让小白越看越迷糊，那还不如不写该教程。
自己会，和把别人教会，是两回事。

教程的标题虽然为Windows上Python数值计算开发环境的基础知识，但讲完配置后，作者还“趁热打铁”给出了深度学习界的入门例子——异或门模型。
毕竟，所有的前期准备工作，最终的目的都是为了应用，我们不是为了配置开发环境而配置开发环境。
这个不能再简单的例子，作为入门，再适合不过。
可谓是，麻雀虽小五脏俱全。
根据终峰定律，结尾的这个实例跟着做完，的确会让学习者产生小有所得的良好感觉。
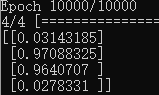
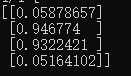
下面是本人训练完模型后用来预测的结果截图。
分别是训练5000和10000个周期后的结果，实际上，示例只有5000，一万是我自己加的，是为了验证“模型的准确率与训练次数呈正相关”这一已知的知识。