deep_learning_neural network梯度下降

神经网络优化算法：梯度下降法、Momentum、RMSprop和Adam

最近回顾神经网络的知识，简单做一些整理，归档一下神经网络优化算法的知识。关于神经网络的优化，吴恩达的深度学习课程讲解得非常通俗易懂，有需要的可以去学习一下，本人只是对课程知识点做一个总结。吴恩达的深度学习课程放在了网易云课堂上，链接如下（免费）：
https://mooc.study.163.com/smartSpec/detail/1001319001.htm

神经网络最基本的优化算法是反向传播算法加上梯度下降法。通过梯度下降法，使得网络参数不断收敛到全局（或者局部）最小值，但是由于神经网络层数太多，需要通过反向传播算法，把误差一层一层地从输出传播到输入，逐层地更新网络参数。由于梯度方向是函数值变大的最快的方向，因此负梯度方向则是函数值变小的最快的方向。沿着负梯度方向一步一步迭代，便能快速地收敛到函数最小值。这就是梯度下降法的基本思想，从下图可以很直观地理解其含义。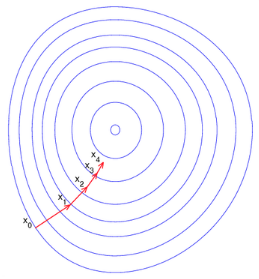

梯度下降法的迭代公式如下：

w=w−α∗dww=w−α∗dw

其中w是待训练的网络参数，αα是学习率，是一个常数，dw是梯度。以上是梯度下降法的最基本形式，在此基础上，研究人员提出了其他多种变种，使得梯度下降法收敛更加迅速和稳定，其中最优秀的代表便是Mommentum, RMSprop和Adam等。

Momentum算法

Momentum算法又叫做冲量算法，其迭代更新公式如下：

{v=βv+(1−β)dww=w−αv{v=βv+(1−β)dww=w−αv

光看上面的公式有些抽象，我们先介绍一下指数加权平均，再回过头来看这个公式，会容易理解得多。

指数加权平均

假设我们有一年365天的气温数据θ1,θ2,...,θ365θ1,θ2,...,θ365，把他们化成散点图，如下图所示：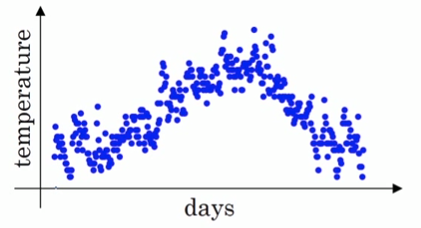

这些数据有些杂乱，我们想画一条曲线，用来表征这一年气温的变化趋势，那么我们需要把数据做一次平滑处理。最常见的方法是用一个华东窗口滑过各个数据点，计算窗口的平均值，从而得到数据的滑动平均值。但除此之外，我们还可以使用指数加权平均来对数据做平滑。其公式如下：

{v0=0vk=βvk−1+(1−β)θk,k=1,2,...,365{v0=0vk=βvk−1+(1−β)θk,k=1,2,...,365

v就是指数加权平均值，也就是平滑后的气温。ββ的典型值是0.9，平滑后的曲线如下图所示：

对于vk=βvk−1+(1−β)θkvk=βvk−1+(1−β)θk，我们把它展开，可以得到如下形式：

vk=βvk−1+(1−β)θk=βkv0+βk−1(1−β)θ1+βk−2(1−β)θ2+⋯+β(1−β)θk−1+(1−β)θk=βk−1(1−β)θ1+βk−2(1−β)θ2+⋯+β(1−β)θk−1+(1−β)θkvk=βvk−1+(1−β)θk=βkv0+βk−1(1−β)θ1+βk−2(1−β)θ2+⋯+β(1−β)θk−1+(1−β)θk=βk−1(1−β)θ1+βk−2(1−β)θ2+⋯+β(1−β)θk−1+(1−β)θk

可见，平滑后的气温，是以往每一天原始气温的加权平均值，只是这个权值是随时间的远近而变化的，离今天越远，权值越小，且呈指数衰减。从今天往前数k天，它的权值为βk(1−β)βk(1−β)。当β=11−ββ=11−β时，由于limβ→1βk(1−β)=e−1limβ→1βk(1−β)=e−1，权重已经非常小，更久远一些的气温数据权重更小，可以认为对今天的气温没有影响。因此，可以认为指数加权平均计算的是最近11−β11−β个数据的加权平均值。通常ββ取值为0.9，相当于计算10个数的加权平均值。但是按照原始的指数加权平均公式，还有一个问题，就是当k比较小时，其最近的数据太少，导致估计误差比较大。例如v1=0.9v0+(1−0.9)θ1=0.1θ1v1=0.9v0+(1−0.9)θ1=0.1θ1。为了减小最初几个数据的误差，通常对于k比较小时，需要做如下修正：

vk=βvk−1+(1−β)θk1−βkvk=βvk−1+(1−β)θk1−βk

1−βk1−βk是所有权重的和，这相当于对权重做了一个归一化处理。下面的图中，紫色的线就是没有做修正的结果，修正之后就是绿色曲线。二者在前面几个数据点之间相差较大，后面则基本重合了。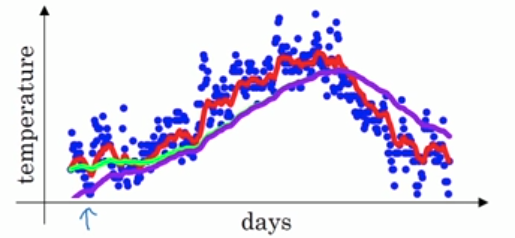

回看Momentum算法

现在再回过头来看Momentum算法的迭代更新公式：

{v=βv+(1−β)dww=w−αv{v=βv+(1−β)dww=w−αv

dwdw是我们计算出来的原始梯度，vv则是用指数加权平均计算出来的梯度。这相当于对原始梯度做了一个平滑，然后再用来做梯度下降。实验表明，相比于标准梯度下降算法，Momentum算法具有更快的收敛速度。为什么呢？看下面的图，蓝线是标准梯度下降法，可以看到收敛过程中产生了一些震荡。这些震荡在纵轴方向上是均匀的，几乎可以相互抵消，也就是说如果直接沿着横轴方向迭代，收敛速度可以加快。Momentum通过对原始梯度做了一个平滑，正好将纵轴方向的梯度抹平了（红线部分），使得参数更新方向更多地沿着横轴进行，因此速度更快。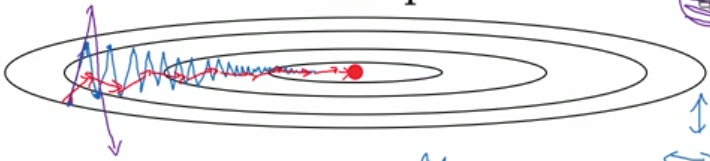

RMSprop算法

对于上面的这个椭圆形的抛物面（图中的椭圆代表等高线），沿着横轴收敛速度是最快的，所以我们希望在横轴（假设记为w1）方向步长大一些，在纵轴（假设记为w2）方向步长小一些。这时候可以通过RMSprop实现，迭代更新公式如下：

{s1=β1s1+(1−β1)dw21s2=β2s2+(1−β2)dw22{s1=β1s1+(1−β1)dw12s2=β2s2+(1−β2)dw22

⎧⎩⎨w1=w1−αdw1s1+ϵ√w2=w2−αdw2s2+ϵ√{w1=w1−αdw1s1+ϵw2=w2−αdw2s2+ϵ

观察上面的公式可以看到，s是对梯度的平方做了一次平滑。在更新w时，先用梯度除以s1+ϵ−−−−−√s1+ϵ，相当于对梯度做了一次归一化。如果某个方向上梯度震荡很大，应该减小其步长；而震荡大，则这个方向的s也较大，除完之后，归一化的梯度就小了；如果某个方向上梯度震荡很小，应该增大其步长；而震荡小，则这个方向的s也较小，归一化的梯度就大了。因此，通过RMSprop，我们可以调整不同维度上的步长，加快收敛速度。把上式合并后，RMSprop迭代更新公式如下：

{s=βs+(1−β)dw2w=w−αdws+ϵ√{s=βs+(1−β)dw2w=w−αdws+ϵ

ββ的典型值是0.999。公式中还有一个ϵϵ，这是一个很小的数，典型值是10−810−8。

Adam算法

Adam算法则是以上二者的结合。先看迭代更新公式：

⎧⎩⎨⎪⎪v=β1v+(1−β1)dws=β2s+(1−β2)dw2w=w−αvs+ϵ√{v=β1v+(1−β1)dws=β2s+(1−β2)dw2w=w−αvs+ϵ

典型值：β1=0.9,β2=0.999,ϵ=10−8β1=0.9,β2=0.999,ϵ=10−8。Adam算法相当于先把原始梯度做一个指数加权平均，再做一次归一化处理，然后再更新梯度值。

转自：https://www.cnblogs.com/jiaxblog/p/9695042.html