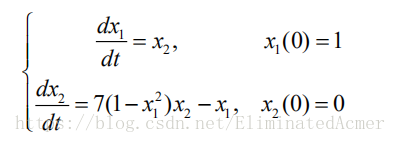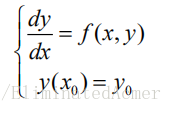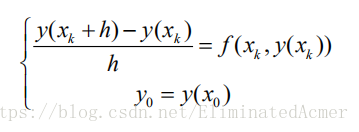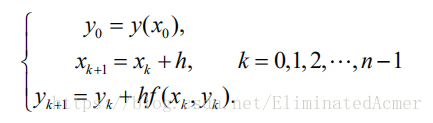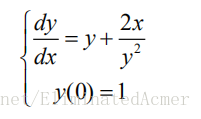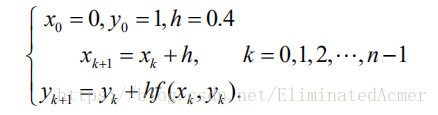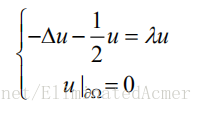Matlab学习——求解微分方程(组)

介绍：

1.在 Matlab 中，用大写字母 D 表示导数，Dy 表示 y 关于自变量的一阶导数，D2y 表示 y 关于自变量的二阶导数，依此类推.函数 dsolve 用来解决常微分方程（组）的求解问题，调用格式为

X=dsolve(‘eqn1’,’eqn2’,…)

如果没有初始条件，则求出通解，如果有初始条件，则求出特解

系统缺省的自变量为 t。

2.函数 dsolve 求解的是常微分方程的精确解法，也称为常微分方程的符号解.但是，有大量的常微分方程虽然从理论上讲，其解是存在的，但我们却无法求出其解析解，此时，我们需要寻求方程的数值解，在求常微分方程数值解方面，MATLAB 具有丰富的函数，将其统称为 solver，其一般格式为：

[T,Y]=solver(odefun,tspan,y0)

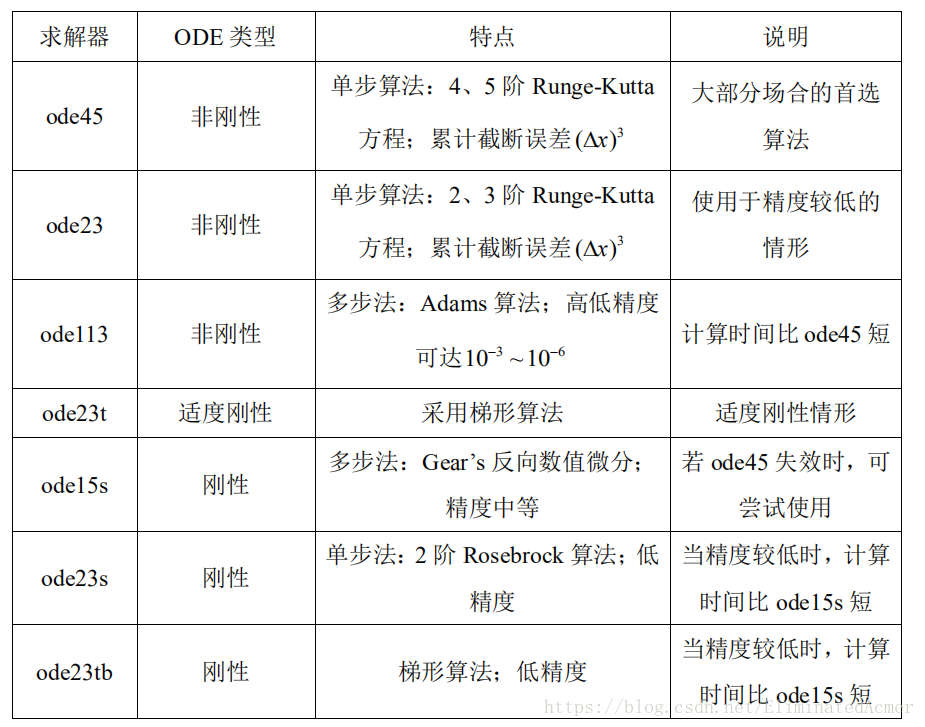
说明：(1)solver 为命令 ode45、ode23、ode113、ode15s、ode23s、ode23t、ode23tb、ode15i 之一.

(2)odefun 是显示微分方程 y '  = f (t , y) 在积分区间 tspan = [t 0 , t f ] 上从 t0 到 t f  用初始条件 y0 求解.

(3)如果要获得微分方程问题在其他指定时间点 t 0 , t1 , t 2 , , t f  上的解，则令tspan = [t 0 , t1 , t 2 , t f ] (要求是单调的).

(4)因为没有一种算法可以有效的解决所有的 ODE 问题，为此，Matlab 提供了多种求解器 solver，对于不同的 ODE 问题，采用不同的 solver

3．在 matlab 命令窗口、程序或函数中创建局部函数时，可用内联函数 inline，inline 函数形式相当于编写 M 函数文件，但不需编写 M-文件就可以描述出某种数学关系.调用 inline 函数，只能由一个 matlab 表达式组成，并且只能返回一个变量，不允许[u,v]这种向量形式.因而，任何要求逻辑运算或乘法运算以求得最终结果的场合，都不能应用 inline 函数，inline 函数的一般形式为：

FunctionName=inline(‘函数内容’, ‘所有自变量列表’)

例如：（求解 F(x)=x^2*cos(a*x)-b ,a,b 是标量；x 是向量 ）在命令窗口输入:

Fofx=inline('x.^2.*cos(a.*x)-b','x','a','b');g = Fofx([pi/ pi/3.5],,)

系统输出为：g=-1.5483 -1.7259注意：由于使用内联对象函数 inline 不需要另外建立 m 文件，所有使用比较方便，另外在使用 ode45 函数的时候，定义函数往往需要编辑一个 m 文件来单独定义，这样不便于管理文件，这里可以使用 inline 来定义函数。

例子：

一、ex(求精确解)：

1. 求解微分方程 y ' + 2xy = xe-x2

syms x y; y=dsolve('Dy+2*x*y=x*exp(-x^2)','x')

运行结果：

2. 求微分方程 xy ' + y - e x  = 0 在初始条件 y (1) = 2e 下的特解并画出解函数的图形.

syms x y; y=dsolve('x*Dy+y-exp(1)=0','y(1)=2*exp(1)','x');ezplot(y)

运行结果：

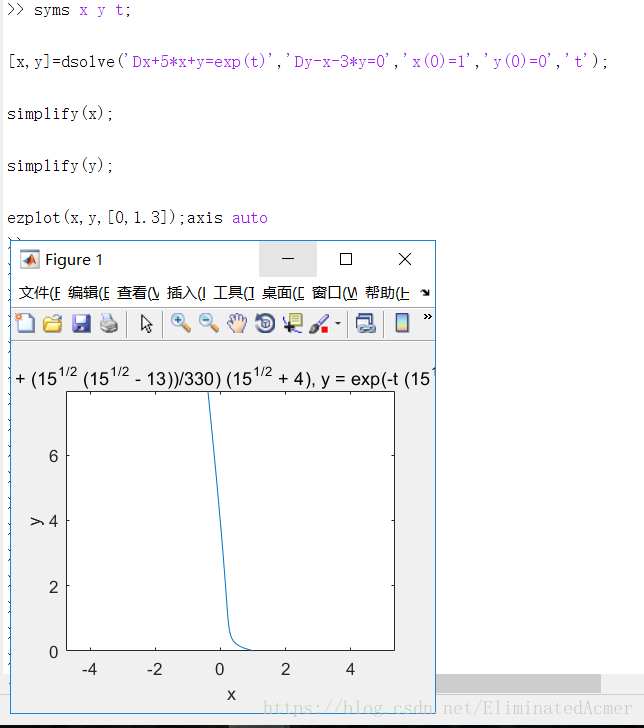
3. 求解微分方程组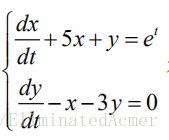在初始条件x |t = 0 = 1, y |t =0 = 0 下的特解,并画出解函数的图像。

syms x y t;

[x,y]=dsolve('Dx+5*x+y=exp(t)','Dy-x-3*y=0','x(0)=1','y(0)=0','t');

simplify(x);

simplify(y);

ezplot(x,y,[,1.3]);axis auto

其中，simplify函数可以对符号表达式进行简化。以下是运行结果：

二、ex(近似解):

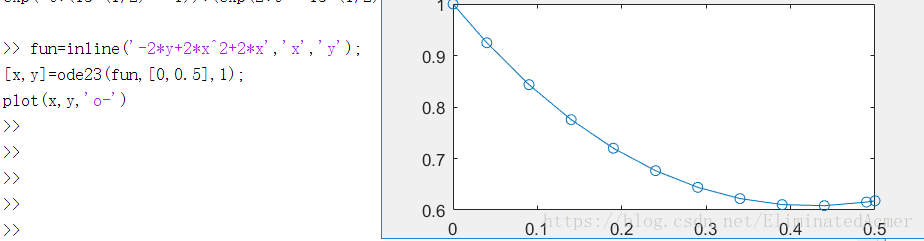
1. 求解微分方程初值问题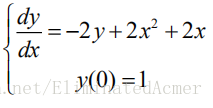的数值解，求解范围为区间 [0,0.5] 。

fun=inline('-2*y+2*x^2+2*x','x','y');
[x,y]=ode23(fun,[,0.5],);
plot(x,y,'o-')

2.求解微分方程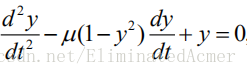，y(0) = 1,y(0) = 0 的解，并画出解的图像。

通过变换，将二阶方程化为一阶方程组求解.令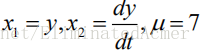，则

编写 vdp.m 文件：

function fy=vdp(t,x)

fy=[x();*(-x()^)*x()-x()];

end

命令行输入：

y0=[;]
[t,x]=ode45('vdp',[,],y0);
y=x(:,);dy=x(:,);
plot(t,y,t,dy)

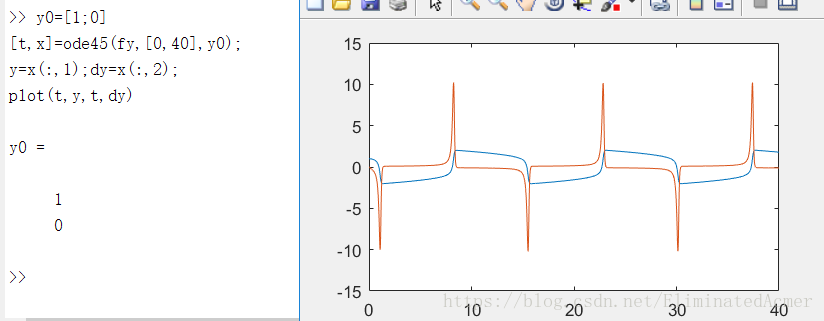
在使用ode45函数的时候,定义函数往往需要编辑一个 .m文件来单独定义,这样不便于管理文件，因此编写 inline 函数：

fy=inline('[x(2);7*(1-x(1)^2)*x(2)-x(1)]','t','x')

运行：

结果一致！

三、ex(用 Euler 折线法求解):

Euler 折线法求解的基本思想是将微分方程初值问题

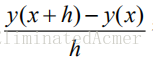
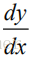
化成一个代数(差分)方程，主要步骤是用差商替代微商，于是

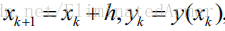
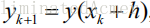
记，从而，于是

1. 用 Euler 折线法求解微分方程初值问题

的数值解（步长h取 0.4），求解范围为区间[0,2]

本题的差分方程为：

clear;
f=sym('y+2*x/y^2');a=;b=;
h=0.4;
n=(b-a)/h+;
x=;
y=;
szj=[x,y];%数值解
for i=:n-
y=y+h*subs(f,{'x','y'},{x,y});%subs，替换函数
x=x+h;
szj=[szj;x,y];
end;
szj;
plot(szj(:,),szj(:,))

说明：替换函数 subs 例如：输入 subs(a+b,a,4) 意思就是把 a 用 4 替换掉，返回 4+b，也可以替换多个变量，例如：subs(cos(a)+sin(b),{a,b},[sym('alpha'),2])分别用字符 alpha 替换 a 和 2 替换 b，返回 cos(alpha)+sin(2)。

偏微分方程解法

Matlab 提供了两种方法解决 PDE 问题，一是使用 pdepe 函数，它可以求解一般的 PDEs,具有较大的通用性，但只支持命令形式调用；二是使用 PDE 工具箱，可以求解特殊 PDE 问题，PDEtoll 有较大的局限性，比如只能求解二阶 PDE问题，并且不能解决片微分方程组，但是它提供了 GUI 界面，从复杂的编程中解脱出来，同时还可以通过 File—>Save As 直接生成 M 代码.

实例：

求解一个正方形区域上的特征值问题：

正方形区域为：。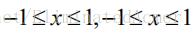

(1)使用 PDE 工具箱打开 GUI 求解方程

(2)进入 Draw 模式，绘制一个矩形，然后双击矩形，在弹出的对话框中设置Left=-1,Bottom=-1,Width=2,Height=2,确认并关闭对话框

(3)进入 Boundary 模式，边界条件采用 Dirichlet 条件的默认值

(4)进入 PDE 模式，单击工具栏 PDE 按钮，在弹出的对话框中方程类型选择Eigenmodes,参数设置 c=1,a=-1/2,d=1,确认后关闭对话框

(5)单击工具栏的 D 按钮，对正方形区域进行初始网格剖分，然后再对网格进一步细化剖分一次

(6)点开 solve 菜单，单击 Parameters 选项，在弹出的对话框中设置特征值区域为[-20,20]

(7)单击 Plot 菜单的 Parameters 项，在弹出的对话框中选中 Color、Height(3-D plot)和 show mesh 项，然后单击 Done 确认

(8)单击工具栏的“=”按钮，开始求解

得到结果：