BZOJ 2127 / Luogu P1646 [国家集训队]happiness (最小割)

题面

BZOJ传送门

Luogu传送门

分析

这道题又出现了二元关系,于是我们只需要解方程确定怎么连边就行了



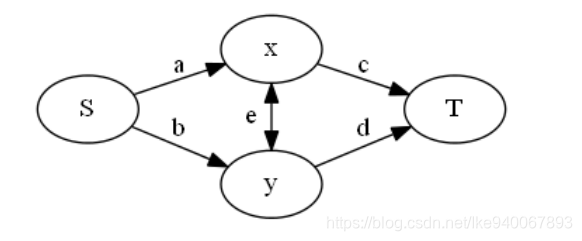
假设跟SSS分在一块是选文科,跟TTT分在一块是选理科,先加上所有的收益,再来考虑如何让需要减去的代价最小.我们来看看代价的方程

定义AAA表示选文科的收益,BBB表示选理科的收益,有:

• a+b=Ax+Ay+Ax,y\large a+b=A_x+A_y+A_{x,y}a+b=Ax​+Ay​+Ax,y​
• c+d=Bx+By+Bx,y\large c+d=B_x+B_y+B_{x,y}c+d=Bx​+By​+Bx,y​
• a+e+d=Ax+By+Ax,y+Bx,y\large a+e+d=A_x+B_y+A_{x,y}+B_{x,y}a+e+d=Ax​+By​+Ax,y​+Bx,y​
• b+e+c=Bx+Ay+Ax,y+Bx,y\large b+e+c=B_x+A_y+A_{x,y}+B_{x,y}b+e+c=Bx​+Ay​+Ax,y​+Bx,y​

能够解出来

• a=Ax+Ax,y2\large a=A_x+\frac{A_{x,y}}2a=Ax​+2Ax,y​​
• b=Ay+Ax,y2\large b=A_y+\frac{A_{x,y}}2b=Ay​+2Ax,y​​
• c=Bx+Bx,y2\large c=B_x+\frac{B_{x,y}}2c=Bx​+2Bx,y​​
• d=By+Bx,y2\large d=B_y+\frac{B_{x,y}}2d=By​+2Bx,y​​
• e=Ax,y2+Bx,y2\large e=\frac{A_{x,y}}2+\frac{B_{x,y}}2e=2Ax,y​​+2Bx,y​​

所以我们只需要把边权乘以二做最小割,然后用所有收益减去最小割的答案除以2就行了.

CODE

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
char cb[1<<15],*cs=cb,*ct=cb;
#define getc() (cs==ct && (ct = (cs = cb) + fread(cb , 1 , 1<<15 , stdin),cs==ct)?0:*cs++)
template<typename T>inline void read(T &num) {
    char ch; while((ch=getchar())<'0'||ch>'9');
    for(num=0;ch>='0'&&ch<='9';num=num*10+ch-'0',ch=getchar());
}

const int inf = 1e9;
const int MAXN = 10005;
const int MAXM = 2000005;
const int dx[] = { 1, -1, 0, 0, 0 };
const int dy[] = { 0, 0, -1, 1, 0 };
int n, m, fir[MAXN], S, T, cnt;
struct edge { int to, nxt; int c; }e[MAXM];
inline void add(int u, int v, int cc, int rc=0) {
	e[cnt] = (edge){ v, fir[u], cc }; fir[u] = cnt++;
	e[cnt] = (edge){ u, fir[v], rc }; fir[v] = cnt++;
}
int dis[MAXN], vis[MAXN], info[MAXN], cur, q[MAXN];
inline bool bfs() {
	int head = 0, tail = 0;
	vis[S] = ++cur; q[tail++] = S;
	while(head < tail) {
		int u = q[head++];
		for(int i = fir[u]; ~i; i = e[i].nxt)
			if(e[i].c && vis[e[i].to] != cur)
				vis[e[i].to] = cur, dis[e[i].to] = dis[u] + 1, q[tail++] = e[i].to;
	}
	if(vis[T] == cur) memcpy(info, fir, (T+1)<<2);
	return vis[T] == cur;
}
int dfs(int u, int Max) {
	if(u == T || !Max) return Max;
	int flow=0, delta;
	for(int &i = info[u]; ~i; i = e[i].nxt)
		if(e[i].c && dis[e[i].to] == dis[u] + 1 && (delta=dfs(e[i].to, min(e[i].c, Max-flow)))) {
			e[i].c -= delta, e[i^1].c += delta, flow += delta;
			if(flow == Max) return flow;
		}
	return flow;
}
inline int dinic() {
	int flow=0, x;
	while(bfs()) {
		while((x=dfs(S, inf))) flow+=x;
	}
	return flow;
}
int sum, tmps[MAXN], tmpt[MAXN], A[105][105], B[105][105];
inline int enc(int i, int j) { return (i-1)*m + j; }
int main () {
	memset(fir, -1, sizeof fir);
	read(n); read(m); S = 0; T = n*m+1;
	for(int i = 1, x; i <= n; ++i)for(int j = 1; j <= m; ++j)read(x), sum += x, tmps[enc(i,j)] += 2*x;
	for(int i = 1, x; i <= n; ++i)for(int j = 1; j <= m; ++j)read(x), sum += x, tmpt[enc(i,j)] += 2*x;
	for(int i = 1; i < n; ++i)for(int j = 1; j <= m; ++j)read(A[i][j]), sum += A[i][j], tmps[enc(i,j)] += A[i][j], tmps[enc(i+1,j)] += A[i][j];
	for(int i = 1; i < n; ++i)for(int j = 1; j <= m; ++j)read(B[i][j]), sum += B[i][j], tmpt[enc(i,j)] += B[i][j], tmpt[enc(i+1,j)] += B[i][j];
	for(int i = 1; i < n; ++i)for(int j = 1; j <= m; ++j)add(enc(i, j), enc(i+1, j), A[i][j]+B[i][j], A[i][j]+B[i][j]);
	for(int i = 1; i <= n; ++i)for(int j = 1; j < m; ++j)read(A[i][j]), sum += A[i][j], tmps[enc(i,j)] += A[i][j], tmps[enc(i,j+1)] += A[i][j];
	for(int i = 1; i <= n; ++i)for(int j = 1; j < m; ++j)read(B[i][j]), sum += B[i][j], tmpt[enc(i,j)] += B[i][j], tmpt[enc(i,j+1)] += B[i][j];
	for(int i = 1; i <= n; ++i)for(int j = 1; j < m; ++j)add(enc(i, j), enc(i, j+1), A[i][j]+B[i][j], A[i][j]+B[i][j]);
	for(int i = 1; i <= n*m; ++i) {
		if(tmps[i]) add(S, i, tmps[i]);
		if(tmpt[i]) add(i, T, tmpt[i]);
	}
	printf("%d\n", sum-dinic()/2);
}