树模型-label boosting-GBDT

GBDT

GBDT是boosting系列算法的代表之一，其核心是 梯度+提升+决策树。

GBDT回归问题

通俗的理解：

先来个通俗理解：假如有个人30岁，我们首先用20岁去拟合，发现损失有10岁，这时我们用6岁去拟合剩下的损失，发现差距还有4岁，第三轮我们用3岁拟合剩下的差距，差距就只有一岁了。如果我们的迭代轮数还没有完，可以继续迭代下面，每一轮迭代，拟合的岁数误差都会减小。最后将每次拟合的岁数加起来便是模型输出的结果。

决策树用的是cart树，准确来说是用的cart树中的回归树。之所以要用回归树，是因为gbdt其实去拟合的不仅仅是原数据的标签，还有每一个树经过学习之后留下的残差：所以gbdt不管是分类还是回归，都是拟合的残差值。GBDT的过程用文字描述是这样的：

假设我拿到一批数据，标签是连续值，我拿来做回归任务。

那么拿到数据之后，gbdt首先开始初始化它的第0颗树，一般而言吗，第0颗树不做什么特殊的操作，输出值就是标签的均值。

初始化好了之后，我们就可以计算每一个样本的第一批残差，严格来说这个值是损失函数对第0颗树求偏导的结果，我们用平方损失作为loss的话就是刚刚训练的那颗树减去标签的值，拿到残差后，，残差作为本次训练样本的新标签，开始建立第一课CART树：

1. 遍历每个特征下所有可能的切分点，寻找最优的切分点之后将样本一分为2，大于这个切分点的样本丢到左子树，小于等于的放右子树，当然也可以反着来，这个看具体的工程实现。
2. 这个时候，我们左右节点都有了样本，那么此刻左右节点还可以接着再分，接着开始按上面的套路接着在所有的特征上再找一遍最优切分点，又把数据一分为2。这个过程直到满足样本不可再分的情况下为止，具体来说，我们可以定义树的深度，每个叶子节点含有的最少样本数等等来限制树的生长过程，不限制的话，基本是就是一直分到只剩下一个样本落到叶子节点上为止。
3. 现在我们已经到了叶子节点了，那么这个叶子节点的值就是其所包含的样本的标签的均值，或者是是餐叉的均值
4. 现在第一颗树已经ok了，那么这颗树的输出值就是: 前面所有树的输出+本次树的输出*学习率，得到最终的输出值
5. 好了之后，我们开始计划训练下一颗树，步骤就是通过再一次计算梯度得到残差，更新这批训练样本的标签，以同样的套路再训练一遍，又得到一颗树。
6. 一直训练，假设我们需要100颗树，那就这样训练100次
7. 最终，预测的时候，我们丢一条样本，进去，每颗树都能得到一个输出值，我们把这些输出值加起来作为最终的预测结果

GBDT的前夜--提升树

提升树算法也是用的残差去拟合下一颗树，它和gbdt的不同是：他真的是残差，而gbdt则是近似残差。那么它的算了步骤是这样的



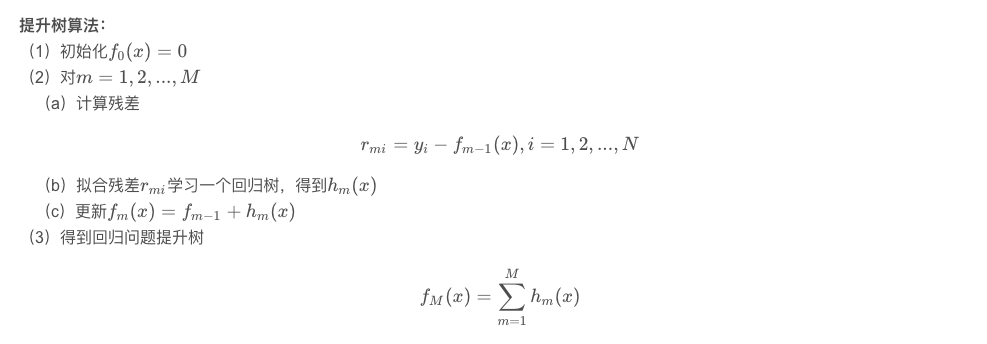
而且，与gbdt相比，其第0课树一般输出是0

GBDT残差近似

其实就是提升树的部分，把残差改成了损失函数的梯度，用来近似提升树的残差。所以，当使用平方损失的时候，这个梯度就是真正的残差，如果boosting算法每一步的弱分类器生成都是依据损失函数的梯度方向，则称之为梯度提升(Gradient boosting)

GBDT 分类问题

这里我们再看看GBDT分类算法，GBDT的分类算法从思想上和GBDT的回归算法没有区别，核心还是用残差去拟合树。但是由于样本输出不是连续的值，而是离散的类别，导致我们无法直接从输出类别去拟合类别输出的误差。

为了解决这个问题，主要有两个方法，一个是用指数损失函数，此时GBDT退化为Adaboost算法。另一种方法是用类似于逻辑回归的对数似然损失函数的方法。也就是说，我们用的是类别的预测概率值和真实概率值的差来拟合损失。这里讨论用对数似然损失函数的GBDT分类。而对于对数似然损失函数，我们又有二元分类和多元分类的区别。

二分类

回归问题上，我们用的损失可能是平方损失，那么在二分类问题上，我们用的损失就是非常经典的逻辑回归的损失，也就是而分类交叉熵损失(BCE loss)，也叫对数似然损失。在预测类别的时候，每棵树我们都能拿到一个叶子节点，叶子节点上存着的和gbdt回归一样，是属于该叶子节点的样本的残差的均值，也就是label的均值，为什么分类也是label的均值？因为分类也是用的回归树，回归树划分叶子节点的损失是平方损失。

同样的，这些树在做预测的时候，也是加法模型，但是最终的预测结果，需要做一件事，激活：显然，我们可以用lr的激活方式也就是sigmoid做激活，拿来搞定二分类问题

损失函数

损失函数拿来做梯度计算，拿到下一批样本的残差即是label，二分类损失函数为：

\[L(Y,f(x))=-\frac{1}{n}\sum [y\ln f(x)+(1-y)\ln (1-f(x))]
\]

激活用sigmoid函数

整个过程描述为：

多分类

与二分类的套路一样，不过需要注意的是，多分类时候，有多少个类，一般一轮都会建多少颗树。

损失函数的话，多分类最长使用的损失函数就是交叉熵了：

\[L(Y,f(x))=-\frac{1}{n}\sum y_i ln f(x)
\]

激活函数用的softmax



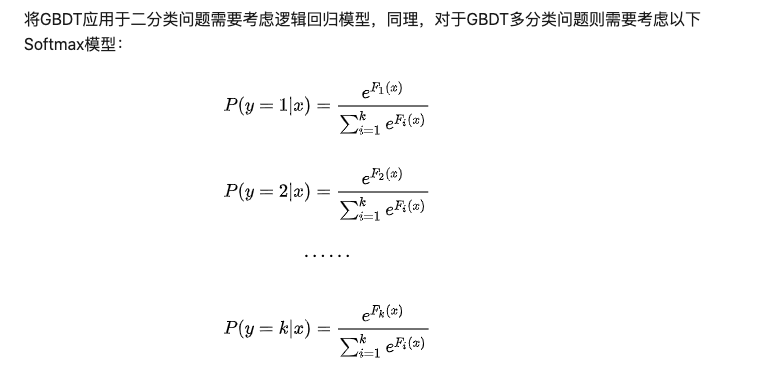
那么整个过程有：

GBDT总结

GBDT主要的优点有：

• 可以灵活处理各种类型的数据，包括连续值和离散值。
• 在相对少的调参时间情况下，预测的准备率也可以比较高。这个是相对SVM来说的。
• 使用一些健壮的损失函数，对异常值的鲁棒性非常强。比如 Huber损失函数和Quantile损失函数。

GBDT的主要缺点有：

• 由于弱学习器之间存在依赖关系，难以并行训练数据。不过可以通过自采样的SGBT来达到部分并行。

GBDT的一些思考

1. gbdt数据需要考虑归一化吗？
   
   理论上来说是不需要的，因为特征做不做归一化，都不会影响到结点是否分裂或者不分裂。分不分只与此刻label的分布造成的分裂点的收益有关

参考链接

gbdt是如何进行多分类的

gbdt多分类

gbdt二分类

gbdt step by step