重新整理数据结构与算法(c#)——算法套路k克鲁斯算法[三十]
前言
这个和前面一节有关系,是这样子的,前面是用顶点作为参照条件,这个是用边作为参照条件。
正文
图解如下:
每次选择最小的边。
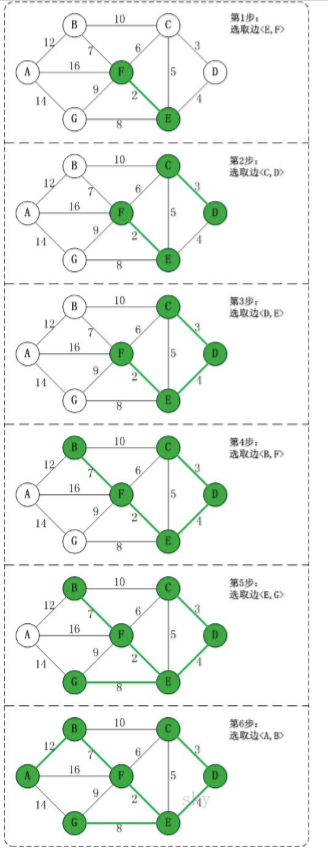
但是会遇到一个小问题,就是会构成回路。
比如说第四步中,最小边是CE,但是没有选择CE,因为CE会形成回路。
那么如何判断是否有回路呢?

判断两个点的终点,是否一致。
这个是怎么来的呢?为什么判断终点是否一致就可以判断有回路呢?
是这样子的,如何两个点可以共同到达任何一个点,那么他们之间一定是通的,这一点是肯定的,如果他们本来就是通的,再在他们之间加一条那么肯定回路的。
那么为什么选择终点呢?是这样子的,假如他们之间选来不相通,他们肯定在两条路上。
假设选了cd和ef这两条路。那么他们这两条路的终点分别是d(c->d)和f(e->f),他们的终点不同,那么他们没有在一条路上,所以把c->d的终点d的终点设置为e->另一条路的终点也就是f,连接后所有节点都有公共的终点,那么终点就可以作为判断依据,这样就不用去遍历了。
代码如下:
private static int INF = int.MaxValue;
static void Main(string[] args)
{
char[] vertexs = { 'A', 'B', 'C', 'D', 'E', 'F', 'G' };
//克鲁斯卡尔算法的邻接矩阵
int[,] matrix = {
/*A*//*B*//*C*//*D*//*E*//*F*//*G*/
/*A*/ { 0, 12, INF, INF, INF, 16, 14},
/*B*/ { 12, 0, 10, INF, INF, 7, INF
},
/*C*/ { INF, 10, 0, 3, 5, 6, INF},
/*D*/ { INF, INF, 3, 0, 4, INF, INF},
/*E*/ { INF, INF, 5, 4, 0, 2, 8},
/*F*/ { 16, 7, 6, INF, 2, 0, 9},
/*G*/ { 14, INF, INF, INF, 8, 9, 0}};
KruskaCase kruskaCase = new KruskaCase(vertexs,matrix);
kruskaCase.kruskal();
Console.ReadKey();
}
}
public class KruskaCase
{
private int edgeNum;//边的个数
private char[] vertexs;//顶点数组
private int[,] matrix;//邻接矩阵
private static int INF = int.MaxValue;
public KruskaCase(char[] vertexs, int[,] matrix)
{
int vlen = vertexs.Length;
//初始化顶点,避免污染数据
this.vertexs = new char[vlen];
for (int i=0;i<vlen;i++)
{
this.vertexs[i] = vertexs[i];
}
//初始化边, 避免污染数据
this.matrix = new int[vlen,vlen];
for (int i = 0; i < vlen; i++)
{
for (int j = 0; j < vlen; j++)
{
this.matrix[i,j] = matrix[i,j];
}
}
for (int i = 0; i < vlen; i++)
{
for (int j = i+1; j < vlen; j++)
{
if (matrix[i, j] != INF)
{
edgeNum++;
}
}
}
}
public void kruskal()
{
//表示第几条边加入最后的结果
int index = 0;
//记录每个顶点的终点
int[] ends = new int[edgeNum];
//最后边的个数肯定是节点数量-1
EData[] result = new EData[vertexs.Length-1];
EData[] edges = getEData();
sortEData(edges);
for (int i=0;i<edgeNum;i++)
{
var start = getPosition(edges[i].start);
var end = getPosition(edges[i].end);
int startEndPoint = getEnd(ends,start);
int endEndPoint = getEnd(ends, end);
if (startEndPoint != endEndPoint)
{
ends[startEndPoint] = endEndPoint;
result[index++] = edges[i];
}
}
Console.WriteLine("最小生成树为:");
for (int i=0;i<result.Length;i++)
{
Console.WriteLine(result[i]);
}
}
private int getPosition(char ch)
{
for (int i = 0; i < vertexs.Length; i++)
{
if (vertexs[i] == ch)
{
return i;
}
}
return -1;
}
private int getEnd(int[] ends, int i)
{ // i = 4 [0,0,0,0,5,0,0,0,0,0,0,0]
while (ends[i] != 0)
{
i = ends[i];
}
return i;
}
/// <summary>
/// 对边数组进行排序
/// </summary>
/// <param name="edges">需要排序的边数组</param>
private void sortEData(EData[] edges)
{
for (int i = 0; i < edges.Length - 1; i++)
{
for (int j = 0; j < edges.Length - 1 - i; j++)
{
if (edges[j].weight > edges[j + 1].weight)
{//交换
EData tmp = edges[j];
edges[j] = edges[j + 1];
edges[j + 1] = tmp;
}
}
}
}
结果:
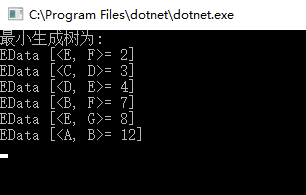
重新整理数据结构与算法(c#)——算法套路k克鲁斯算法[三十]的更多相关文章
- 数据结构与算法系列研究五——树、二叉树、三叉树、平衡排序二叉树AVL
树.二叉树.三叉树.平衡排序二叉树AVL 一.树的定义 树是计算机算法最重要的非线性结构.树中每个数据元素至多有一个直接前驱,但可以有多个直接后继.树是一种以分支关系定义的层次结构. a.树是n ...
- 数据结构- 串的模式匹配算法:BF和 KMP算法
数据结构- 串的模式匹配算法:BF和 KMP算法 Brute-Force算法的思想 1.BF(Brute-Force)算法 Brute-Force算法的基本思想是: 1) 从目标串s 的第一个字 ...
- C基础 算法实现层面套路
引言 - 从实践狗讲起 理论到实践(有了算法到实现) 中间有很多过程. 算法方面本人啥也不懂, 只能说说实现方面. 例如下面 一个普通的插入排序. // // 插入排序默认从大到小 // extern ...
- C语言二级选择题考点汇总-数据结构与算法-【考点一】 什么是算法
1.算法及其基本特征 算法是指对方案的准确描述,是解决问题的执行步骤. 算法不等于数学上的计算方法,也不等于程序.程序是算法的载体. 算法的基本特征如下: (1)可行性:步骤可实现,执行结果可达到 ...
- 深入浅出数据结构C语言版(2)——简要讨论算法的时间复杂度
所谓算法的"时间复杂度",你可以将其理解为算法"要花费的时间量".比如说,让你用抹布(看成算法吧--)将家里完完全全打扫一遍大概要5个小时,那么你用抹布打扫家里 ...
- 【算法总结】强化学习部分基础算法总结(Q-learning DQN PG AC DDPG TD3)
总结回顾一下近期学习的RL算法,并给部分实现算法整理了流程图.贴了代码. 1. value-based 基于价值的算法 基于价值算法是通过对agent所属的environment的状态或者状态动作对进 ...
- 基于改进人工蜂群算法的K均值聚类算法(附MATLAB版源代码)
其实一直以来也没有准备在园子里发这样的文章,相对来说,算法改进放在园子里还是会稍稍显得格格不入.但是最近邮箱收到的几封邮件让我觉得有必要通过我的博客把过去做过的东西分享出去更给更多需要的人.从论文刊登 ...
- 推荐一个算法编程学习中文社区-51NOD【算法分级,支持多语言,可在线编译】
最近偶尔发现一个算法编程学习的论坛,刚开始有点好奇,也只是注册了一下.最近有时间好好研究了一下,的确非常赞,所以推荐给大家.功能和介绍看下面介绍吧.首页的标题很给劲,很纯粹的Coding社区....虽 ...
- 《算法导论》读书笔记之图论算法—Dijkstra 算法求最短路径
自从打ACM以来也算是用Dijkstra算法来求最短路径了好久,现在就写一篇博客来介绍一下这个算法吧 :) Dijkstra(迪杰斯特拉)算法是典型的最短路径路由算法,用于计算一个节点到其他所有节点的 ...
- K Nearest Neighbor 算法
文章出处:http://coolshell.cn/articles/8052.html K Nearest Neighbor算法又叫KNN算法,这个算法是机器学习里面一个比较经典的算法, 总体来说KN ...
随机推荐
- 搭建一个Java项目可直接拿去使用的通用工具类
1.通用枚举类 import lombok.Getter; /** * @Description 状态码定义约束,共6位数,前三位代表服务,后3位代表接口 * 比如 商品服务210,购物车是220.用 ...
- echart 带表格
"echarts": "^5.2.2", ChartSituation1 <template> <div> <EChartTemp ...
- 深入浅出Java多线程(十二):线程池
引言 大家好,我是你们的老伙计秀才!今天带来的是[深入浅出Java多线程]系列的第十二篇内容:线程池.大家觉得有用请点赞,喜欢请关注!秀才在此谢过大家了!!! 在现代软件开发中,多线程编程已经成为应对 ...
- Spring 中不得不了解的姿势
说明 本文非原创,我只是进行了整理以及做了一些改动,仅供学习,若需进行商业使用,请联系原作者 原作者:苏三 原文链接:苏三说技术:Spring系列 Spring IOC 本章节解读的流程为Spring ...
- CMake的作用和价值--概念简介
一 简介: CMake是一个跨平台的安装(编译)工具,可以用简单的语句来描述所有平台的安装(编译过程).他能够输出各种各样的makefile或者project文件,能测试编译器所支持的C++特性,类似 ...
- day02-MySQL基础知识
MySQL基本知识 1.数据库 1.1.创建数据库 语法: CREATE DATABASE [IF NOT EXISTS] db_name [create_specification[,create_ ...
- window10-yarn-使用vite创建vue3项目失败-文件夹或目录不正确
前置条件 window10 本地已经安装nodejs yarn已经通过npm全局安装(npm install -g yarn) 问题 yarn脚手架方式搭建vue3项目失败(command faile ...
- 记录--vue3问题:如何实现微信扫码授权登录?
这里给大家分享我在网上总结出来的一些知识,希望对大家有所帮助 一.需求 微信扫码授权,如果允许授权,则登录成功,跳转到首页. 二.问题 1.微信扫码授权有几种实现方式? 2.说一下这几种实现方式的原理 ...
- 记录-JavaScript常规加密技术
这里给大家分享我在网上总结出来的一些知识,希望对大家有所帮助 当今Web开发中,数据安全是一个至关重要的问题,为了确保数据的安全性,我们需要使用加密技术.JavaScript作为一种客户端编程语言,可 ...
- 鸿蒙HarmonyOS实战-ArkUI组件(Row/Column)
前言 HarmonyOS的布局组件是一组用于构建用户界面布局的组件,包括线性布局.相对布局.网格布局等.这些组件帮助开发者以简单和灵活的方式管理和组织应用程序中的视图,并支持多种不同的设备屏幕尺寸和方 ...
