【路径规划】OSQP曲线平滑 公式及代码

参考与前言

---

1. apollo 代码：https://github.com/ApolloAuto/apollo/tree/master/modules/planning/math/smoothing_spline

2. apollo readme：https://github.com/ApolloAuto/apollo/blob/master/docs/specs/qp_spline_path_optimizer.md

3. 自我测试的代码：张聪明/OSQP_test (gitee.com)

本篇也主要基于参考二翻译而来，背景是因为 GPIR代码 里有这层做初始化，不太懂怎么干的和干啥，所以就搜索了一下，一开始一直在弄参考三使其能逐步断点debug 以让我能明了整个步骤，不过后来搜了一下看到了参考二 emm 就是我想要了解的 smooth到底是怎样编程二次规划问题的。

以下大部分翻译至参考二，其中添加了自己的思考句子（有时也可能就是问题

实际这个包的名字就：QP-Spline-Path Optimizer，基于二次规划的曲线路径优化器

方法：Quadratic programming + Spline interpolation，二次规划 + 样条差值

注意这全文都是讲的path，而不是trajectory，至于两者区别：Motion Planning 是什么 总结了下：

Path是静态的，不包括时间；Trajectory是除了路径还有其他信息可以说是时间，speed profile，这条路径上速度的变化关系

这一段是我看完了写的：emmm 看完了发现包装的太好了 以至于就算看了整个公式 对应起来都是要跳转进去的 果然是做软件一套的。但是想着用的话 这样也算是够了的。所以整体其实还是拿五次样条先生成了reference point 然后根据他们的s,l点来进行约束，cost function也已经给出

① 目标函数 Objective function

路径长度

首先路径的坐标系是以SL 也就是frenet坐标系下。其中 s 是从车辆当前位置到规划路径的长度，类似于我们会提前给定一个 我们要规划多长的距离。

样条线段

将路径拆分成 n 段。每段都用多项式表示，比如这样一个式子：

每段 i 沿着参考线的累积距离 \(d_i\) 的多项式函数公式如下：

\[l = f_i(s)
= a_{i0} + a_{i1} \cdot s + a_{i2} \cdot s^2 + a_{i3} \cdot s^3 + a_{i4} \cdot s^4 + a_{i5} \cdot s^5 (0 \leq s \leq d_{i}) \tag{1}
\]

实际代码调用时，后者的 5 也就是五次多项式的意思

OsqpSpline2dSolver osqp_spline2d_solver(t_knots, 5);

线段的优化函数

也就是一个cost 和为速度，加速度，加加速度：

\[\begin{align}
cost = \sum_{i=1}^{n} \Big( w_1 \cdot \int\limits_{0}^{d_i} (f_i')^2(s) ds + w_2 \cdot \int\limits_{0}^{d_i} (f_i'')^2(s) ds +
w_3 \cdot \int\limits_{0}^{d_i} (f_i^{\prime\prime\prime})^2(s) ds \Big)
\end{align}
\]

但实际test.cc这个代码中只对加加速度进行了weight赋值，所以最后在计算曲率 curvature的时候 smooth后的效果明显好很多（虽然点之间看不出来啥）

mutable_kernel->Add2dThirdOrderDerivativeMatrix(0.5);

将cost函数转为QP形式

QP formulation:

\[\begin{aligned}
minimize & \frac{1}{2} \cdot x^T \cdot H \cdot x + f^T \cdot x \\
s.t. \qquad & LB \leq x \leq UB \\
& A_{eq}x = b_{eq} \\
& Ax \geq b
\end{aligned}
\]

下面是如何被优化函数objective function/cost function转成QP形式，首先我们 (1)式 可以转成向量相乘的形式，那么 \(f_i(s)\) 可以这样表示

\[f_i(s) ＝
\begin{vmatrix} 1 & s & s^2 & s^3 & s^4 & s^5 \end{vmatrix}
\cdot
\begin{vmatrix} a_{i0} \\ a_{i1} \\ a_{i2} \\ a_{i3} \\ a_{i4} \\ a_{i5} \end{vmatrix}
\]

\(f_i'(s)\) 求导再次表示

\[f_i'(s) =
\begin{vmatrix} 0 & 1 & 2s & 3s^2 & 4s^3 & 5s^4 \end{vmatrix}
\cdot
\begin{vmatrix} a_{i0} \\ a_{i1} \\ a_{i2} \\ a_{i3} \\ a_{i4} \\ a_{i5} \end{vmatrix}
\]

\(f_i'(s)^2\) 两个相乘一下：

\[f_i'(s)^2 =
\begin{vmatrix} a_{i0} & a_{i1} & a_{i2} & a_{i3} & a_{i4} & a_{i5} \end{vmatrix}
\cdot
\begin{vmatrix} 0 \\ 1 \\ 2s \\ 3s^2 \\ 4s^3 \\ 5s^4 \end{vmatrix}
\cdot
\begin{vmatrix} 0 & 1 & 2s & 3s^2 & 4s^3 & 5s^4 \end{vmatrix}
\cdot
\begin{vmatrix} a_{i0} \\ a_{i1} \\ a_{i2} \\ a_{i3} \\ a_{i4} \\ a_{i5} \end{vmatrix}
\]

然后就会获得这样的：

\[\int\limits_{0}^{d_i} f_i'(s)^2 ds ＝
\int\limits_{0}^{d_i}
\begin{vmatrix} a_{i0} & a_{i1} & a_{i2} & a_{i3} & a_{i4} & a_{i5} \end{vmatrix}
\cdot
\begin{vmatrix} 0 \\ 1 \\ 2s \\ 3s^2 \\ 4s^3 \\ 5s^4 \end{vmatrix}
\cdot
\begin{vmatrix} 0 & 1 & 2s & 3s^2 & 4s^3 & 5s^4 \end{vmatrix}
\cdot
\begin{vmatrix} a_{i0} \\ a_{i1} \\ a_{i2} \\ a_{i3} \\ a_{i4} \\ a_{i5} \end{vmatrix} ds
\]

把常数项提到积分外面去：

\[\int\limits_{0}^{d_i} f'(s)^2 ds ＝
\begin{vmatrix} a_{i0} & a_{i1} & a_{i2} & a_{i3} & a_{i4} & a_{i5} \end{vmatrix}
\cdot
\int\limits_{0}^{d_i}
\begin{vmatrix} 0 \\ 1 \\ 2s \\ 3s^2 \\ 4s^3 \\ 5s^4 \end{vmatrix}
\cdot
\begin{vmatrix} 0 & 1 & 2s & 3s^2 & 4s^3 & 5s^4 \end{vmatrix} ds
\cdot
\begin{vmatrix} a_{i0} \\ a_{i1} \\ a_{i2} \\ a_{i3} \\ a_{i4} \\ a_{i5} \end{vmatrix}
\]

\[＝\begin{vmatrix} a_{i0} & a_{i1} & a_{i2} & a_{i3} & a_{i4} & a_{i5} \end{vmatrix}
\cdot \int\limits_{0}^{d_i}
\begin{vmatrix}
0 & 0 &0&0&0&0\\
0 & 1 & 2s & 3s^2 & 4s^3 & 5s^4\\
0 & 2s & 4s^2 & 6s^3 & 8s^4 & 10s^5\\
0 & 3s^2 & 6s^3 & 9s^4 & 12s^5&15s^6 \\
0 & 4s^3 & 8s^4 &12s^5 &16s^6&20s^7 \\
0 & 5s^4 & 10s^5 & 15s^6 & 20s^7 & 25s^8
\end{vmatrix} ds
\cdot
\begin{vmatrix} a_{i0} \\ a_{i1} \\ a_{i2} \\ a_{i3} \\ a_{i4} \\ a_{i5} \end{vmatrix}
\]

然后给矩阵里的都积分一下从0到\(d_i\) 积分一下 就可以获得这样的：

\[\int\limits_{0}^{d_i}
f'_i(s)^2 ds =\begin{vmatrix} a_{i0} & a_{i1} & a_{i2} & a_{i3} & a_{i4} & a_{i5} \end{vmatrix}
\cdot \begin{vmatrix}
0 & 0 & 0 & 0 &0&0\\
0 & d_i & d_i^2 & d_i^3 & d_i^4&d_i^5\\
0& d_i^2 & \frac{4}{3}d_i^3& \frac{6}{4}d_i^4 & \frac{8}{5}d_i^5&\frac{10}{6}d_i^6\\
0& d_i^3 & \frac{6}{4}d_i^4 & \frac{9}{5}d_i^5 & \frac{12}{6}d_i^6&\frac{15}{7}d_i^7\\
0& d_i^4 & \frac{8}{5}d_i^5 & \frac{12}{6}d_i^6 & \frac{16}{7}d_i^7&\frac{20}{8}d_i^8\\
0& d_i^5 & \frac{10}{6}d_i^6 & \frac{15}{7}d_i^7 & \frac{20}{8}d_i^8&\frac{25}{9}d_i^9
\end{vmatrix}
\cdot
\begin{vmatrix} a_{i0} \\ a_{i1} \\ a_{i2} \\ a_{i3} \\ a_{i4} \\ a_{i5} \end{vmatrix}
\]

所以现在应该发现了：如果是五次样条曲线的导数cost函数是会获得一个\(6\times6\)的矩阵

② 约束 Constraints

初始点/end点约束

init point/初始点

假设第一个点是 (\(s_0\), \(l_0\)), (\(s_0\), \(l'_0\)) and (\(s_0\), \(l''_0\)), 其中 \(l_0\) , \(l'_0\) and \(l''_0\) 是规划初始点的横向offset及其一阶导、二阶导，可以由 \(f_i(s)\), \(f'_i(s)\), and \(f_i(s)''\) 计算得知

使用这个式子，将这些约束转为QP等式约束

\[A_{eq}x = b_{eq}
\]

下面就是转换的步骤：

\[f_i(s_0) =
\begin{vmatrix} 1 & s_0 & s_0^2 & s_0^3 & s_0^4&s_0^5 \end{vmatrix}
\cdot
\begin{vmatrix} a_{i0} \\ a_{i1} \\ a_{i2} \\ a_{i3} \\ a_{i4} \\ a_{i5}\end{vmatrix} = l_0
\]

\[f'_i(s_0) =
\begin{vmatrix} 0& 1 & 2s_0 & 3s_0^2 & 4s_0^3 &5 s_0^4 \end{vmatrix}
\cdot
\begin{vmatrix} a_{i0} \\ a_{i1} \\ a_{i2} \\ a_{i3} \\ a_{i4} \\ a_{i5} \end{vmatrix} = l'_0
\]

\[f''_i(s_0) =
\begin{vmatrix} 0&0& 2 & 3\times2s_0 & 4\times3s_0^2 & 5\times4s_0^3 \end{vmatrix}
\cdot
\begin{vmatrix} a_{i0} \\ a_{i1} \\ a_{i2} \\ a_{i3} \\ a_{i4} \\ a_{i5} \end{vmatrix} = l''_0
\]

其中 \(i\) 是指那段拥有初始点 \(s_0\) 的分段区，应该说是最初的那段，因为后面平滑约束的时候还有 \(f_{k+1}(s_0)\)上面三个一起形成了一个等式，即最后的形式如 式(2).

end point/结束点

与上述的initial point 初始点步骤一致，结束点 \((s_e, l_e)\) 也是已知的，而且应该是和前面的约束一致的形式，所以总一总可以得出

等式约束 \(A_{eq}x = b_{eq}\) 展开为以下形式

\[\begin{vmatrix}
1 & s_0 & s_0^2 & s_0^3 & s_0^4&s_0^5 \\
0&1 & 2s_0 & 3s_0^2 & 4s_0^3 & 5s_0^4 \\
0& 0&2 & 3\times2s_0 & 4\times3s_0^2 & 5\times4s_0^3 \\
1 & s_e & s_e^2 & s_e^3 & s_e^4&s_e^5 \\
0&1 & 2s_e & 3s_e^2 & 4s_e^3 & 5s_e^4 \\
0& 0&2 & 3\times2s_e & 4\times3s_e^2 & 5\times4s_e^3
\end{vmatrix}
\cdot
\begin{vmatrix} a_{i0} \\ a_{i1} \\ a_{i2} \\ a_{i3} \\ a_{i4} \\ a_{i5} \end{vmatrix}
=
\begin{vmatrix}
l_0\\
l'_0\\
l''_0\\
l_e\\
l'_e\\
l''_e\\
\end{vmatrix}\tag{2}
\]

实际代码中为：

// init point constraint
mutable_constraint->Add2dPointConstraint(0, Eigen::Vector2d(spline(a, 0), spline(b, 0)));
mutable_constraint->Add2dPointDerivativeConstraint(0, Eigen::Vector2d(spline_1st(a, 0), spline_1st(b, 0)));

// end point constraint
mutable_constraint->Add2dPointConstraint(t_end, Eigen::Vector2d(spline(a, t_end), spline(b, t_end)));
mutable_constraint->Add2dPointDerivativeConstraint(t_end, Eigen::Vector2d(spline_1st(a, t_end), spline_1st(b, t_end)));

分段之间平滑约束

这部分的约束主要在于将分段点连接处进行平滑操作，比如一阶连续，二阶连续，三阶连续。

假设 \(seg_k\) 和 \(seg_{k+1}\) 是相连接的, \(seg_k\) 段累积的 s 距离值为 \(s_k\). 注意这里的 \(s_0\) 不同与前面说的为整段路径的init point初始点，而是每段自身的起点处，所以对 \(seg_k\) 来说他的累积距离 \(s_k\) 正是 \(seg_{k+1}\) 的起点 \(s_0\)

\[f_k(s_k) = f_{k+1} (s_0)
\]

以下为计算过程：

\[\begin{vmatrix}
1 & s_k & s_k^2 & s_k^3 & s_k^4&s_k^5 \\
\end{vmatrix}
\cdot
\begin{vmatrix}
a_{k0} \\ a_{k1} \\ a_{k2} \\ a_{k3} \\ a_{k4} \\ a_{k5}
\end{vmatrix}
=
\begin{vmatrix}
1 & s_{0} & s_{0}^2 & s_{0}^3 & s_{0}^4&s_{0}^5 \\
\end{vmatrix}
\cdot
\begin{vmatrix}
a_{k+1,0} \\ a_{k+1,1} \\ a_{k+1,2} \\ a_{k+1,3} \\ a_{k+1,4} \\ a_{k+1,5}
\end{vmatrix}
\]

\[\begin{vmatrix}
1 & s_k & s_k^2 & s_k^3 & s_k^4&s_k^5 & -1 & -s_{0} & -s_{0}^2 & -s_{0}^3 & -s_{0}^4&-s_{0}^5\\
\end{vmatrix}
\cdot
\begin{vmatrix}
a_{k0} \\ a_{k1} \\ a_{k2} \\ a_{k3} \\ a_{k4} \\ a_{k5} \\ a_{k+1,0} \\ a_{k+1,1} \\ a_{k+1,2} \\ a_{k+1,3} \\ a_{k+1,4} \\ a_{k+1,5}
\end{vmatrix}
= 0
\]

使用 \(s_0\) = 0 在上式中，然后同样添加如下的等式约束：

\[f'_k(s_k) = f'_{k+1} (s_0)
\\
f''_k(s_k) = f''_{k+1} (s_0)
\\
f'''_k(s_k) = f'''_{k+1} (s_0)
\]

实际代码中只添加了三阶连续：(但是三阶连续的前提不是一二阶也连续吗？)

mutable_constraint->Add2dThirdDerivativeSmoothConstraint();

对采样点的边界约束

沿着路径均匀采样 m 个点，检查这些点是否触碰到了障碍物的边界，然后将其转成QP问题的不等式约束：

\[Ax \geq b
\]

首先根据道路宽度和周围障碍物找到点 \((s_j, l_j)\) and \(j\in[0, m]\) 的下边界 \(l_{lb,j}\)，然后不等式约束的计算如下：

\[\begin{vmatrix}
1 & s_0 & s_0^2 & s_0^3 & s_0^4&s_0^5 \\
1 & s_1 & s_1^2 & s_1^3 & s_1^4&s_1^5 \\
...&...&...&...&...&... \\
1 & s_m & s_m^2 & s_m^3 & s_m^4&s_m^5 \\
\end{vmatrix} \cdot \begin{vmatrix}a_{i0} \\ a_{i1} \\ a_{i2} \\ a_{i3} \\ a_{i4} \\ a_{i5} \end{vmatrix}
\geq
\begin{vmatrix}
l_{lb,0}\\
l_{lb,1}\\
...\\
l_{lb,m}\\
\end{vmatrix} \tag{10}
\]

• 为什么会有下界？根据采样的想法应该只有上界才对，或者说下界可以为完全不进行横向采样扩张

  杰哥回复：这是一个box形状，不是说从0-10是我的采样增加区间 而是以ref为0，-10 - 10采样增加区间

• 为什么实际代码中是横纵向都有限制？采样点扩张如上问中

      lower_bound.emplace_back(d_lateral - lat_tol[i]);
      lower_bound.emplace_back(d_longitudinal - lon_tol[i]);
  
      upper_bound.emplace_back(d_lateral + lat_tol[i]);
      upper_bound.emplace_back(d_longitudinal + lon_tol[i]);
  

  如此手绘图所示：

  

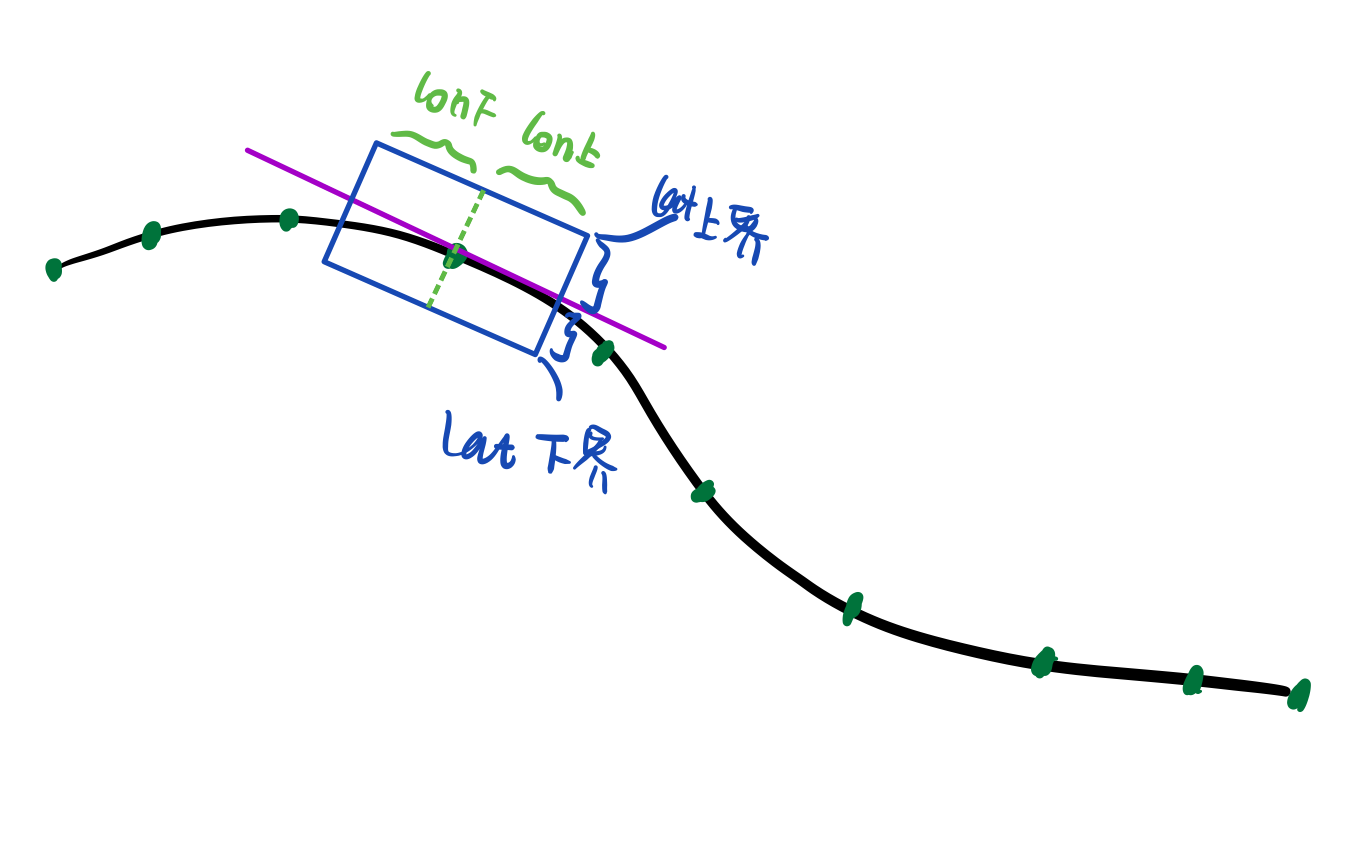
• 这里没有办法根据障碍物加进去边界条件？

  好像可以对某一个 \(l_{ub,j}\) 进行扩大，使其表达障碍物的膨胀。但是我感觉这个点应该是说已知环境中，不包括动态障碍物，类似于在地图已经建好的这层上去做边界约束，而不是实时根据障碍物去做约束

  这样的 因为输入的边界约束是station lateral boundary，其实是依据你的reference line 参考线然后有设定纵向和横向的最大便宜角度进去，比如test代码中是0.2

同样的，上界 \(l_{ub,j}\) 同样也可以以这种不等式约束计算：

\[\begin{vmatrix}
-1 & -s_0 & -s_0^2 & -s_0^3 & -s_0^4&-s_0^5 \\
-1 & -s_1 & -s_1^2 & -s_1^3 & -s_1^4&-s_1^5 \\
...&...-&...&...&...&... \\
-1 & -s_m & -s_m^2 & -s_m^3 & -s_m^4&-s_m^5 \\
\end{vmatrix}
\cdot
\begin{vmatrix} a_{i0} \\ a_{i1} \\ a_{i2} \\ a_{i3} \\ a_{i4} \\ a_{i5} \end{vmatrix}
\geq
-1 \cdot
\begin{vmatrix}
l_{ub,0}\\
l_{ub,1}\\
...\\
l_{ub,m}\\
\end{vmatrix} \tag{11}
\]

③ 代码总结

首先完整的test代码可见gitee链接，此处仅将上述提到的进行说明

  // solver
  OsqpSpline2dSolver osqp_spline2d_solver(t_knots, 5);

  mutable_kernel->Add2dReferenceLineKernelMatrix(t_coord, ref_ft, 0.5);

  // 添加连续平滑约束 三阶
  mutable_constraint->Add2dThirdDerivativeSmoothConstraint();

  // 添加初始点
  mutable_constraint->Add2dPointConstraint(0, Eigen::Vector2d(spline(a, 0), spline(b, 0)));
  mutable_constraint->Add2dPointDerivativeConstraint(0, Eigen::Vector2d(spline_1st(a, 0), spline_1st(b, 0)));

  // 添加end point
  double t_end = t_coord.back();
  mutable_constraint->Add2dPointConstraint(t_end, Eigen::Vector2d(spline(a, t_end), spline(b, t_end)));
  mutable_constraint->Add2dPointDerivativeConstraint(t_end, Eigen::Vector2d(spline_1st(a, t_end), spline_1st(b, t_end)));

  // 添加边界约束
  mutable_constraint->Add2dStationLateralBoundary(t_coord, ref_ft, ref_theta,lon_tol, lat_tol);

实际上看上去 数学公式都被隐去了 是因为osqp这层 apollo加了自己的spline，所以最后main呈现的就是这样的形式，如果跳转各个部分的更为仔细的可以发现更多，比如添加边界约束：

bool Spline2dConstraint::Add2dStationLateralBoundary(
    const std::vector<double>& t, const vector_Eigen<Eigen::Vector2d>& ref_xy,
    const std::vector<double>& ref_theta, const std::vector<double>& lon_tol,
    const std::vector<double>& lat_tol) {
  if (t.size() != ref_xy.size() || ref_xy.size() != ref_theta.size() ||
      ref_theta.size() != lon_tol.size() || lon_tol.size() != lat_tol.size()) {
    return false;
  }

  Eigen::MatrixXd sl_constraints =
      Eigen::MatrixXd::Zero(2 * t.size(), total_param_);
  std::vector<double> lower_bound, upper_bound;

  for (uint32_t i = 0; i < t.size(); ++i) {
    const uint32_t index = FindSegStartIndex(t[i]);
    const double d_lateral = SignDistance(ref_xy[i], ref_theta[i]);
    const double d_longitudinal =
        SignDistance(ref_xy[i], ref_theta[i] - M_PI_2);
    const double t_corrected = t[i] - t_knots_[index];

    std::vector<double> lateral_coef = AffineCoef(ref_theta[i], t_corrected);
    std::vector<double> longitudianl_coef =
        AffineCoef(ref_theta[i] - M_PI_2, t_corrected);

    const uint32_t index_offset = index * spline_param_num_;

    // 构建公式10,11的左边矩阵
    for (uint32_t j = 0; j < spline_param_num_; ++j) {
      sl_constraints(2 * i, index_offset + j) = lateral_coef[j];
      sl_constraints(2 * i, index_offset + total_param_ / 2 + j) =
          lateral_coef[spline_param_num_ + j];
      sl_constraints(2 * i + 1, index_offset + j) = longitudianl_coef[j];
      sl_constraints(2 * i + 1, index_offset + total_param_ / 2 + j) =
          longitudianl_coef[spline_param_num_ + j];
    }

    lower_bound.emplace_back(d_lateral - lat_tol[i]);
    lower_bound.emplace_back(d_longitudinal - lon_tol[i]);

    upper_bound.emplace_back(d_lateral + lat_tol[i]);
    upper_bound.emplace_back(d_longitudinal + lon_tol[i]);
  }

  return coxy_constraint_.AddConstraint(sl_constraints, lower_bound,
                                        upper_bound);
}

由这里我们可以看到公式 10 和公式 11的矩阵形式的构建

④ 效果示意

运行上面给的Gitee代码，可以得到下面这样一幅图：

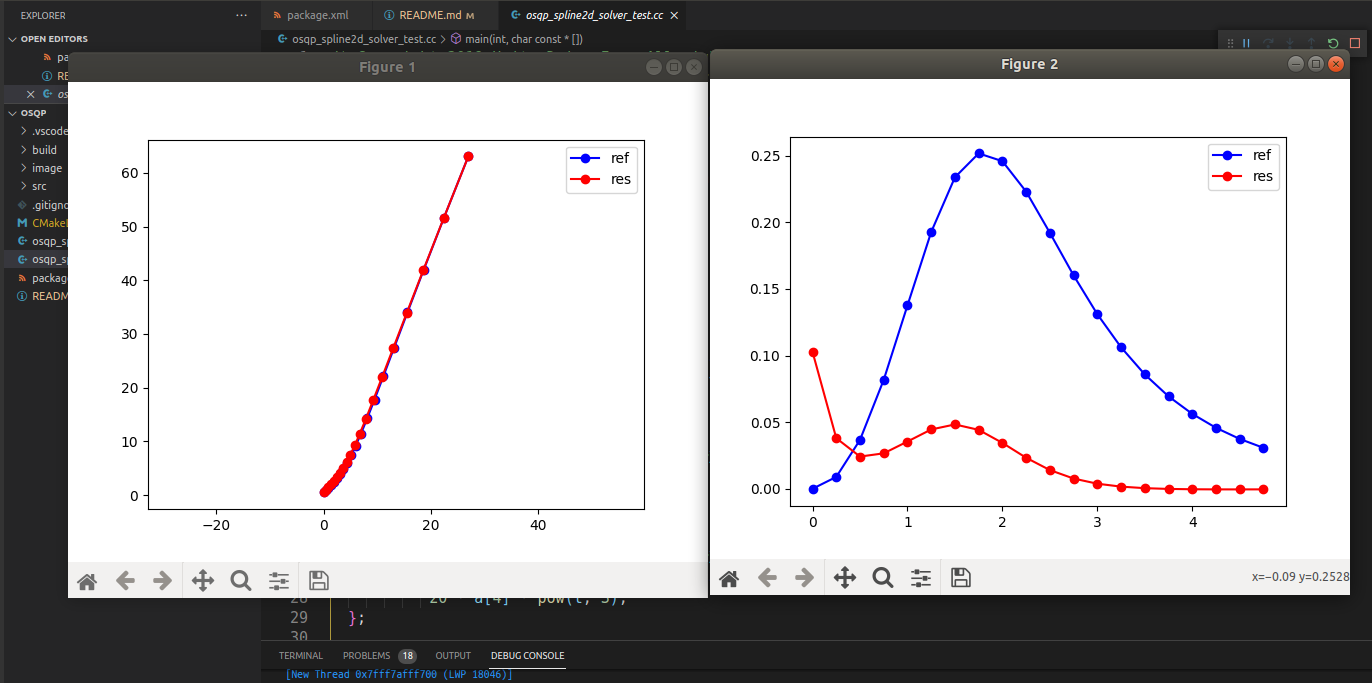
ref就是每小段都是五次样条出来的，做图就是sl坐标系下生成出来的，右图为计算了他们的每个点连接处的曲率，可以看到经过osqp spline曲率约束 cost 都有明显的生效（虽然在这个例子中展现的不大）