Set Concept

集合（Set）就是一种用来装事物的容器（或者称为结构），它所装的东西叫元素。集合这个容器的逻辑性很强，可以说是现在比较严谨的工具。

集合里的元素，它们可以是任何类型的数学对象：数字、符号、变量、空间中的点、线、面，甚至是其他集合，当然它也可以不是数学对象，一些其他事物。

规定：

• 元素通常用 a, b, c, d, x等小写字母来表示；

• 而集合通常用A, B, C, D, X等大写字母来表示。 一些大写字母已经约定俗成的表示某类数，比如Q是有理数，R是实数，C是复数，I是虚数...

集合的表示

集合的表示无非是想给这个容器定义好边界、大小，让人能一眼看出它里面能装多少个多大、多小的数字。

常见的表示方式：

• 描述法
  
  可以用文字描述，比如： A = 大于零的前三个自然数
  
  也可以用数学符号描述，比如： A = {x|x>0 且 x<4}
• 列举法
  
  直接罗列出来，比如：{1,2,3}

集合的三特性

集合概念众多，但是它的三特性必须得记住:

• 无序性：集合中的元素没有特定的顺序，集合中的元素之间没有先后之分。
• 互异性：集合中的元素是互不相同的，即集合中不会出现重复的元素。
• 确定性：对于任意一个元素，要么它属于集合，要么它不属于集合，不存在模棱两可的情况。

元素与集合的关系

元素与集合的关系只有两种，不存在其他模棱两可的情况：

• 属于 ∈
• 不属于 ∉

集合间的关系

集合与集合之间的基本关系只有两种：

• 相等 =
• 包含
• 真包含

基于集合间的关系，衍生出一些集合的概念，我们逐个来了解一下:

• 空集 ∅ 、 {}
  
  就是说这个集合里面什么都不包含；

• 子集 （Subset）
  
  
  
  符号类似 A ≤ B

• 真子集（Proper Subset）
  
  

  举例理解真子集：
  
  假设有两个集合A = {1, 2} 和 B = {1, 2, 3}。

  A是B的子集，因为A中的所有元素（1和2）都属于B。
  
  A不是B的真子集，因为A和B相等，即 A = B。
  
  B是A的真子集，因为B包含了A中的所有元素，并且还有额外的元素3。

• 等集
  
  

• 超集（Superset）
  
  超集是指包含一个或多个集合的集合。如果集合A的所有元素也同时属于集合B，那么集合B被称为集合A的超集。

  超集和真子集的区别？
  
  真子集是一个更严格的概念，它要求除了包含集合A的所有元素外，还必须存在至少一个额外的元素不属于A。
  
  而超集仅要求包含集合A的所有元素，没有限制其他元素的存在。

• 全集（Universal Set）
  
  全集是指在特定上下文中涵盖了所有讨论范围内元素的集合。
  
  全集通常用符号U表示。在不同的领域和问题中，会改变符号代称。

• 幂集（Power Set）
  
  幂集是指一个集合所有子集的集合。换句话说，给定一个集合A，幂集P(A)是由A的所有可能子集所构成的集合。

  例如，对于集合A = {1, 2}，它的幂集P(A)包含以下子集：
  
  P(A) = {∅, {1}, {2}, {1, 2}}
  
  其中，∅表示空集，{1}表示只包含元素1的子集，{2}表示只包含元素2的子集，{1, 2}表示包含元素1和元素2的子集。

集合间的运算

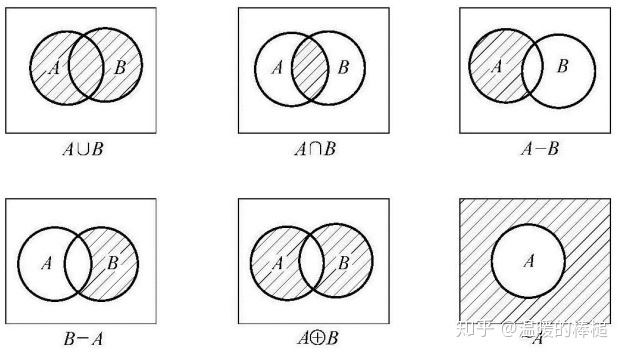
• 并集 ∪

• 交集 ∩

• 补集
  
  

• 差集