代码随想录Day1

704.二分查找

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例 1:

输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

示例 2:

输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

提示：

你可以假设 nums 中的所有元素是不重复的。

n 将在 [1, 10000]之间。

nums 的每个元素都将在 [-9999, 9999]之间。

---

暴力

从头到尾循环一遍，找到了就返回下标，否则返回-1（代码略）；

Obviously，此算法时间复杂度为\(O(n)\),数据较大时就TLE挂了QwQ；

那么如何优化呢?

再来仔细地读一遍题目，发现题目中有一个很重要的条件没用：

给定的\(n\)个元素是有序的！

二分法(正解)

顾名思义，“二分法”的核心思想就是每次将搜索范围减小一半，以达到节省时间的目的；

因为数据是有序的，所以可以将数据的大小作为关键字与目标\(target\)进行比较分类；

具体过程就是将区间中点\(mid\)与\(target\)比较：

当\(target=mid\)时返回下标；

当\(target<mid\)时搜索左半边；

当\(target>mid\)时搜索右半边；

时间复杂度\(O(log_2n)\)

注意：整个过程需要基于数组有序！！！

上代码(●'◡'●)

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int l=0,r=nums.size()-1;//l:区间左边界；r:区间右边界
        while(l<=r){//二分
            int mid=(l+r)>>1;//找中点（">>"位运算符号，相当于/2）
            if(nums[mid]==target){
                return mid;
            }
            if(nums[mid]<target){
                l=mid+1;
            }
            if(nums[mid]>target){
                r=mid-1;
            }
        }
        return -1;
    }
};//完结撒花ヾ(≧▽≦*)o

35.搜索插入位置

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为\(O(log n)\) 的算法。

示例 1:

输入: nums = [1,3,5,6], target = 5
输出: 2

示例 2:

输入: nums = [1,3,5,6], target = 2
输出: 1

示例 3:

输入: nums = [1,3,5,6], target = 7
输出: 4

提示:

\(1 <= nums.length <= 10^4\)

\(-10^4 <= nums[i] <= 10^4\)

nums 为 无重复元素 的 升序 排列数组

\(-10^4 <= target <= 10^4\)

---

正解（still，二分）

由题意得：

一、目标存在：二分查找；

二、目标不存在：返回第一个比目标大的元素下标；

至于第二条怎么实现，其实直接查找结束后返回\(l\)就行啦;

证明：略（其实自己也不知道为什么 QAQ 乱搞出奇迹啦~）

注意：二分法必须基于数据的有序，如果题目没说有序就不能用啦 =)

上代码(●'◡'●)

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int l=0,r=nums.size()-1;
        if(target<nums[0]){
            return 0;
        }
        while(l<=r){//二分，无需多言
            int mid=(l+r)>>1;
            if(nums[mid]==target){
                return mid;
            }
            if(nums[mid]<target){
                l=mid+1;
            }
            if(nums[mid]>target){
                r=mid-1;
            }
        }
        return l;//玄学
    }
};//完结撒花ヾ(≧▽≦*)o

\(O(log_2n)\)跑的真快○( ＾皿＾)っHiahiahia…

34.在排序数组中查找元素的第一个和最后一个位置

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为\(O(log n)\) 的算法解决此问题。

示例 1：

输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]

示例 2：

输入：nums = [5,7,7,8,8,10], target = 6
输出：[-1,-1]

示例 3：

输入：nums = [], target = 0
输出：[-1,-1]

提示：

\(0 <= nums.length <= 10^5\)

\(-10^9 <= nums[i] <= 10^9\)

nums 是一个非递减数组

\(-10^9 <= target <= 10^9\)

---

暴力

还是循环一遍数组，记录下目标第一次后最后一次出现的位置然后输出（代码略）；

Still，obviously，时间复杂度\(O(n)\)，题目可是要求\(O(log_2n)\)的鸭qWq；

BUT！！！数组是有序的；

SO！！！

正解（二分，again）

思路很简单，用两次二分，分别找出第一次出现和最后一次；

上代码(●'◡'●)

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        int l=0,r=nums.size()-1;
        if(r<0){//特判
            return vector<int>{-1,-1};
        }
        int lx,rx,flag=0;
        while(l<=r){//二分查找第一次出现
            int mid=(l+r)>>1;
            if(nums[mid]==target){
                r=mid-1;
                lx=mid;
                flag=1;
            }
            if(nums[mid]>target){
                r=mid-1;
                lx=mid;
            }
            if(nums[mid]<target){
                l=mid+1;
            }
        }
        if(flag==0){//特判，没有这个元素
            return vector<int>{-1,-1};
        }
        l=0,r=nums.size()-1;//初始化
        while(l<=r){//二分查找最后一次出现
            int mid=(l+r)>>1;
            if(nums[mid]==target||nums[mid]<target){
                l=mid+1;
                rx=mid;
            }
            if(nums[mid]>target){
                r=mid-1;
            }
        }
        return vector<int>{lx,rx};//返回答案
    }
};//完结撒花ヾ(≧▽≦*)o

27.移除元素

给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素。元素的顺序可能发生改变。然后返回 nums 中与 val 不同的元素的数量。

假设 nums 中不等于 val 的元素数量为 k，要通过此题，您需要执行以下操作：

更改 nums 数组，使 nums 的前 k 个元素包含不等于 val 的元素。nums 的其余元素和 nums 的大小并不重要。

返回 k。

用户评测：

评测机将使用以下代码测试您的解决方案：

int[] nums = [...]; // 输入数组
int val = ...; // 要移除的值
int[] expectedNums = [...]; // 长度正确的预期答案。
                            // 它以不等于 val 的值排序。

int k = removeElement(nums, val); // 调用你的实现

assert k == expectedNums.length;
sort(nums, 0, k); // 排序 nums 的前 k 个元素
for (int i = 0; i < actualLength; i++) {
    assert nums[i] == expectedNums[i];
}

如果所有的断言都通过，你的解决方案将会 通过。

示例 1：

输入：nums = [3,2,2,3], val = 3
输出：2, nums = [2,2,_,_]
解释：你的函数函数应该返回 k = 2, 并且 nums 中的前两个元素均为 2。

你在返回的 k 个元素之外留下了什么并不重要（因此它们并不计入评测）。

示例 2：

输入：nums = [0,1,2,2,3,0,4,2], val = 2
输出：5, nums = [0,1,4,0,3,_,_,_]
解释：你的函数应该返回 k = 5，并且 nums 中的前五个元素为 0,0,1,3,4。

注意这五个元素可以任意顺序返回。

你在返回的 k 个元素之外留下了什么并不重要（因此它们并不计入评测）。

提示：

0 <= nums.length <= 100

0 <= nums[i] <= 50

0 <= val <= 100

---

暴力

每删除一个元素就将这个元素后所有元素前移；

显然复杂度\(O(n^2)\),TLE没跑了；

正解（快慢指针+左右双指针）

快慢指针：

快指针：寻找新数组的元素 ，新数组就是不含有目标元素的数组

慢指针：指向更新 新数组下标的位置

具体过程：



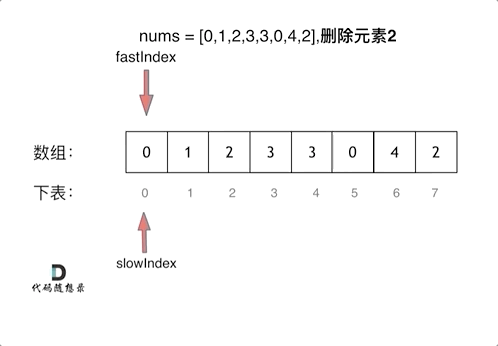
这样写出来的代码：

// 时间复杂度：O(n)
// 空间复杂度：O(1)
class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        int slowIndex = 0;
        for (int fastIndex = 0; fastIndex < nums.size(); fastIndex++) {
            if (val != nums[fastIndex]) {
                nums[slowIndex++] = nums[fastIndex];
            }
        }
        return slowIndex;
    }
};//nice

自己闲来无事，又搞了一个小小的优化（码的好丑不堪入目QwQ）：

class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        int k=0,n=nums.size();
        if(n==0){
            return 0;
        }
        if(n==1){
            if(n==val){
                return 0;
            }
            else{
                return 1;
            }
        }
        int nums1[100000]={0};
        if(n%2==1){//处理数组长度为奇数情况
            if(nums[n/2]!=val){
                nums1[k]=nums[n/2];
                k++;
            }
        }
        for(int i=0,j=n-1;i<n/2;i++,j--){//快指针，从两边往中间，减少一半执行次数
            if(nums[i]!=val){
                nums1[k]=nums[i];
                k++;//慢指针
            }
            if(nums[j]!=val){
                nums1[k]=nums[j];
                k++;
            }
        }
        if(n%2==1){
            nums[n/2]=nums1[n/2];
        }
        for(int i=0,j=n-1;i<n/2;i++,j--){//因为是从两边往中间所以没法和上面的合并/_ \
            nums[i]=nums1[i];//更新
            nums[j]=nums1[j];
        }

        return k;//返回不被删除元素个数
    }
};//完结撒花ヾ(≧▽≦*)o

复杂度\(O(n/2)\),虽然丑了点儿，但跑的贼快^ O ^nice~

977.有序数组的平方

给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

示例 1：

输入：nums = [-4,-1,0,3,10]
输出：[0,1,9,16,100]
解释：平方后，数组变为 [16,1,0,9,100]
排序后，数组变为 [0,1,9,16,100]

示例 2：

输入：nums = [-7,-3,2,3,11]
输出：[4,9,9,49,121]

提示：

\(1 <= nums.length <= 10^4\)

\(-10^4 <= nums[i] <= 10^4\)

nums 已按 非递减顺序 排序

进阶：

请你设计时间复杂度为 \(O(n\)) 的算法解决本问题

暴力

遍历，平方，排序；

复杂度=快排复杂度=\(O(nlog_2n)\);

依旧可以使用双指针优化；

正解（双指针）

数组一开始有序，但平方的大小由绝对值决定

上代码(●'◡'●)

class Solution {
public:
    vector<int> sortedSquares(vector<int>& nums) {
        int r=nums.size()-1,l=0,k=r;//左右指针和结果指针
        vector<int> ans(r+1,0);//结果数组
        while(l<=r){
            if(abs(nums[l])<abs(nums[r])){//先把前面比自己小的存进去
                ans[k] = nums[r]*nums[r];
                k--;
                r--;
            }
            else{//再把自己存进去
                ans[k]=nums[l]*nums[l];
                k--;
                l++;
            }
        }
        return ans;返回结果
    }
};//完结撒花ヾ(≧▽≦*)o

时间复杂度现在也是降到了\(O(n)\),比暴力快了不少！

写博不易，请大佬点赞支持一下8~