JZYZ作业好题

文章目录

• • 敲砖块
  • Circle

敲砖块

首先把砖块向左对齐， 这样选择第

(

i

,

j

)

(i,j)

(i,j)块的前提是第

(

i

−

1

,

j

)

,

(

i

−

1

,

j

+

1

)

(i - 1, j),(i - 1,j + 1)

(i−1,j),(i−1,j+1)被选

满足敲掉的砖块总代价最大，显然是动态规划，接下来我们思考如何设计状态

按照正常的思路应当是

f

[

i

]

[

j

]

f[i][j]

f[i][j]表示到第

i

i

i行一共选择

j

j

j个的最大价值，但是选择第

i

i

i行的每一个所对应的

f

[

i

−

1

]

[

]

f[i-1][]

f[i−1][]的状态和选择都不一样，且很不好维护最值(貌似还要容斥)

我们尝试更改状态，思考敲掉一个砖块需要哪些被敲掉

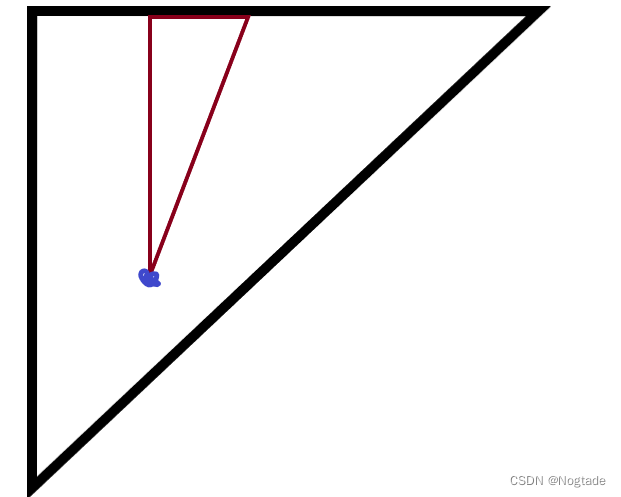
若敲掉蓝色点

(

i

,

j

)

(i,j)

(i,j)，显然第

j

j

j至少敲掉前

i

i

i个， 第

j

+

1

j + 1

j+1列至少敲掉前

i

−

1

i - 1

i−1个，依次类推

所以我们发现，如果按列考虑，不仅可以保证一定可以敲掉，而且统计答案非常方便

设计状态

f

[

i

]

[

j

]

[

k

]

f[i][j][k]

f[i][j][k]表示第

i

i

i列，敲掉前

j

j

j个且一共敲掉前

k

k

k的最大价值

则

f

[

i

]

[

j

]

[

k

]

=

m

a

x

(

f

[

i

+

1

]

[

s

]

[

k

−

j

]

+

s

u

m

[

j

]

[

i

]

,

s

≥

j

−

1

)

f[i][j][k]= max(f[i+1][s][k-j]+sum[j][i],s\ge j-1)

f[i][j][k]=max(f[i+1][s][k−j]+sum[j][i],s≥j−1)，

s

u

m

[

j

]

[

i

]

sum[j][i]

sum[j][i]表示第j列取前

i

i

i个的价值

复杂度为

n

5

n^5

n5，但是跑不满，应该除以一个至少为4的常数，所以能跑过，不过枚举

s

s

s可以优化掉，这样就变成

n

4

n^4

n4

#include<bits/stdc++.h> //竖着看
using namespace std;
#define LL long long
const int MAX = 55;
int f[MAX][MAX][MAX * MAX]; //先i列，第i列选j个，总数为 k
int n, m, a[MAX][MAX], Num[MAX];
int sum[MAX][MAX], ans = 0;
int main() {
	freopen("brike.in","r",stdin);
	freopen("brike.out","w",stdout);
	scanf("%d%d", &n, &m);
	for(int i = 1; i <= n; i++)
		for(int j = 1; j <= (n - i + 1); j++) {
			scanf("%d", &a[i][j]);
			sum[i][j] = sum[i - 1][j];
			sum[i][j] += a[i][j];
		}
	for(int i = 1; i <= n; i++) Num[i] = Num[i - 1] + i;
	for(int i = n; i >= 1; i--) { //第i列
		for(int j = 0; j <= (n - i + 1); j++) { //第i列选j个
			for(int k = Num[j]; k <= m; k++) { //选择总数
				for(int s = j - 1; s <= ((n - i)); s++) { //上一列选多少
					if(j == 0) { f[i][j][k] = max(f[i + 1][max(0, s)][k], f[i][j][k]); }
					else  if(k - j >= 0) f[i][j][k] = max(f[i][j][k], f[i + 1][s][k - j] + sum[j][i]);
					ans = max(ans, f[i][j][k]);
				}
			}
		}
	}
	cout<<ans<<endl;
	return 0;
}

Circle

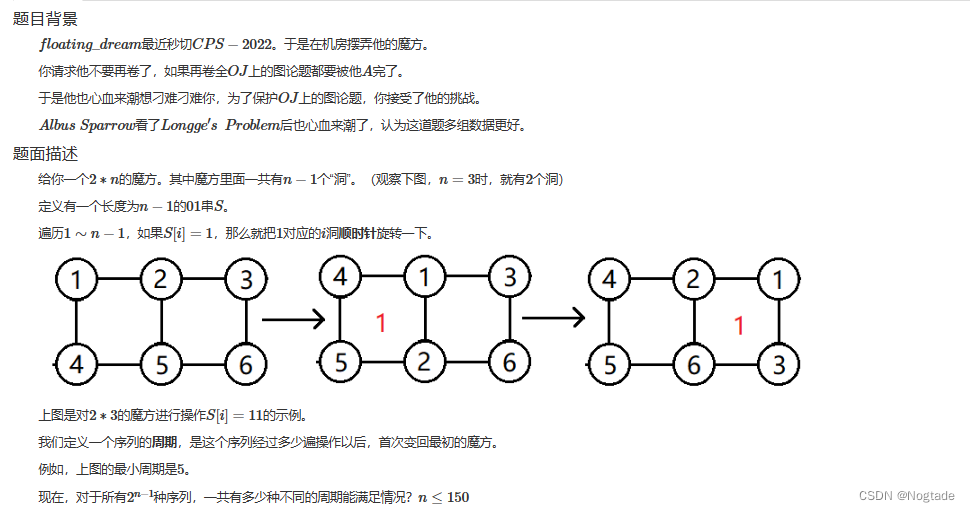
这道题难的就是问题转化

如果一个序列为

101001100

101001100

101001100,我们发现答案就是由

0

0

0隔开的连续

1

1

1的周期的

l

c

m

lcm

lcm

那么一段连续

1

1

1的方格的周期是多少，手玩可得

c

n

t

+

3

cnt+3

cnt+3,

c

n

t

cnt

cnt为连续

1

1

1的个数

那么问题就转化为了

∑

c

n

t

i

<

=

150

\sum cnt_i<=150

∑cnti​<=150,

l

c

m

(

c

n

t

1

+

3

,

c

n

t

2

+

3

,

c

n

t

3

+

3...

)

lcm(cnt_1+3,cnt_2+3,cnt_3+3...)

lcm(cnt1​+3,cnt2​+3,cnt3​+3...)的个数

设计状态

f

[

i

]

f[i]

f[i]表示前

i

i

i个位置的

l

c

m

lcm

lcm个数，且

i

i

i个位置一定放

1

1

1

发现，

l

c

m

(

c

n

t

)

lcm(cnt)

lcm(cnt)最大也不会爆

L

L

LL

LL,最大的为选择5个30左右的质数相乘

考虑用

s

e

t

set

set转移，

f

[

i

]

f[i]

f[i]表示前

i

i

i个位置且第

i

i

i个位置一定放

1

1

1的

l

c

m

lcm

lcm种类

那么考虑第

i

i

i个位置会向前填充多少

j

j

j个连续的

1

1

1,为保证状态的合法，

f

[

i

]

f[i]

f[i]应由

f

[

j

−

1

]

f[j-1]

f[j−1]转移而来，保证

i

i

i向前的是单独的一段，解释起来太麻烦了，直接看代码

	f[0].insert(1);//初始化
	f[1].insert(1);
	for(int i = 2; i <= 150; i++) {
		for(int j = i - 2; j >= 0; j--) { //保证是单独的一段
			for(auto k : f[j]) {
				LL lcmnow = (1LL * k * (i - j + 2) / __gcd(k, 1LL * (i - j + 2)));
				f[i].insert(lcmnow);
			}
		}
	}
	for(int i = 1; i <= 150; i++) {
		printf("%d ,\n", f[i].size()); //size即为答案
		for(auto y : f[i]) {
			f[i + 1].insert(y);//后面可以不填，对i个位置，f[i-1],f[i-2],f[i-3]..的答案也是合法的，类似前缀搞一下
		}
	}

做完发现时间复杂度偏高，但是150非常小，直接打表即可

//问题转化， 转方格的周期 == lcm(ai + 3)的个数
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int MAX = 160;
unordered_set<LL> f[MAX];
int ans[151] = {
0,
1 ,
2 ,
3 ,
4 ,
6 ,
8 ,
11 ,
13 ,
18 ,
21 ,
26 ,
31 ,
37 ,
45 ,
51 ,
58 ,
66 ,
78 ,
88 ,
100 ,
114 ,
128 ,
145 ,
163 ,
180 ,
200 ,
222 ,
245 ,
274 ,
305 ,
333 ,
367 ,
402 ,
443 ,
486 ,
529 ,
574 ,
629 ,
686 ,
741 ,
807 ,
872 ,
939 ,
1016 ,
1100 ,
1184 ,
1277 ,
1371 ,
1476 ,
1593 ,
1708 ,
1826 ,
1962 ,
2100 ,
2246 ,
2408 ,
2571 ,
2745 ,
2939 ,
3129 ,
3331 ,
3556 ,
3780 ,
4018 ,
4279 ,
4547 ,
4826 ,
5129 ,
5440 ,
5773 ,
6127 ,
6477 ,
6861 ,
7279 ,
7693 ,
8134 ,
8610 ,
9092 ,
9606 ,
10160 ,
10709 ,
11296 ,
11926 ,
12563 ,
13252 ,
13979 ,
14704 ,
15480 ,
16306 ,
17148 ,
18043 ,
18975 ,
19920 ,
20950 ,
22031 ,
23112 ,
24270 ,
25492 ,
26718 ,
28038 ,
29424 ,
30815 ,
32303 ,
33862 ,
35451 ,
37152 ,
38906 ,
40686 ,
42602 ,
44597 ,
46612 ,
48765 ,
50991 ,
53269 ,
55715 ,
58222 ,
60770 ,
63504 ,
66323 ,
69185 ,
72257 ,
75410 ,
78619 ,
82047 ,
85591 ,
89214 ,
93045 ,
96967 ,
101005 ,
105318 ,
109711 ,
114201 ,
118995 ,
123890 ,
128930 ,
134279 ,
139725 ,
145307 ,
151253 ,
157314 ,
163550 ,
170152 ,
176876 ,
183799 ,
191137 ,
198616 ,
206295 ,
214387 ,
222649 ,
231205};
int main() {
	freopen("circle.in","r",stdin);
	freopen("circle.out","w",stdout);
	int n;
	while(~scanf("%d", &n)) {
		printf("%d\n", ans[n]);
	}
//	f[0].insert(1);
//	f[1].insert(1);
//	for(int i = 2; i <= 150; i++) {
//		for(int j = i - 2; j >= 0; j--) {
//			for(auto k : f[j]) {
//				LL lcmnow = (1LL * k * (i - j + 2) / __gcd(k, 1LL * (i - j + 2)));
//				f[i].insert(lcmnow);
//			}
//		}
//		printf("i %d \n", i);
//	}
//		printf("***\n");
//	for(int i = 1; i <= 150; i++) {
//		printf("%d ,\n", f[i].size());
//		for(auto y : f[i]) {
//			f[i + 1].insert(y);
//		}
//	}

	return 0;
}