Diffusion Model扩散模型
1、扩散模型基本原理:
扩散模型包括两个步骤:
固定的(或预设的)前向扩散过程q:该过程会逐渐将高斯噪声添加到图像中,直到最终得到纯噪声。
2.可训练的反向去噪扩散过程pθ:训练一个神经网络,从纯噪音开始逐渐去噪,直到得到一个真实图像 。
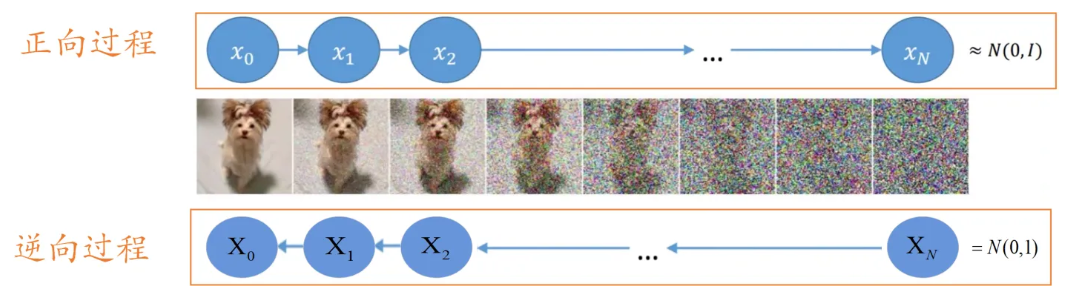
正向过程
首先,对于一张原始图片,我们给加一个高斯噪声,图片由变成x1。【注意:这里必须要加高斯噪声,因为高斯噪声服从高斯分布,后面的一些运算需要用到高斯分布的一些特性】,重复上述添加高斯噪声步骤,直到图片变成xn,由于添加了足够多的高斯噪声,现在的近似服从高斯分布(又称正态分布)。
每一步添加高斯噪声的量一直是不变的吗? 答案是每步添加高斯噪声的量是变化的,且后一步比前一步添加的高斯噪声更多。我想这一点你通过上图也非常容易理解,一开始原图比较干净,我们添加少量高斯噪声就能对原图产生干扰;但越往后高斯噪声量越多,如果还添加一开始少量的高斯噪声,那么这时对上一步结果基本不会产生任何影响。【注:后文所述的每个时刻图像和这里的每一步图像都是一个意思,如时刻图像表示的就是这个图像】
逆向过程
首先,我们会随机生成一个服从高斯分布的噪声图片,然后一步一步的减少噪声直到生成预期图片。

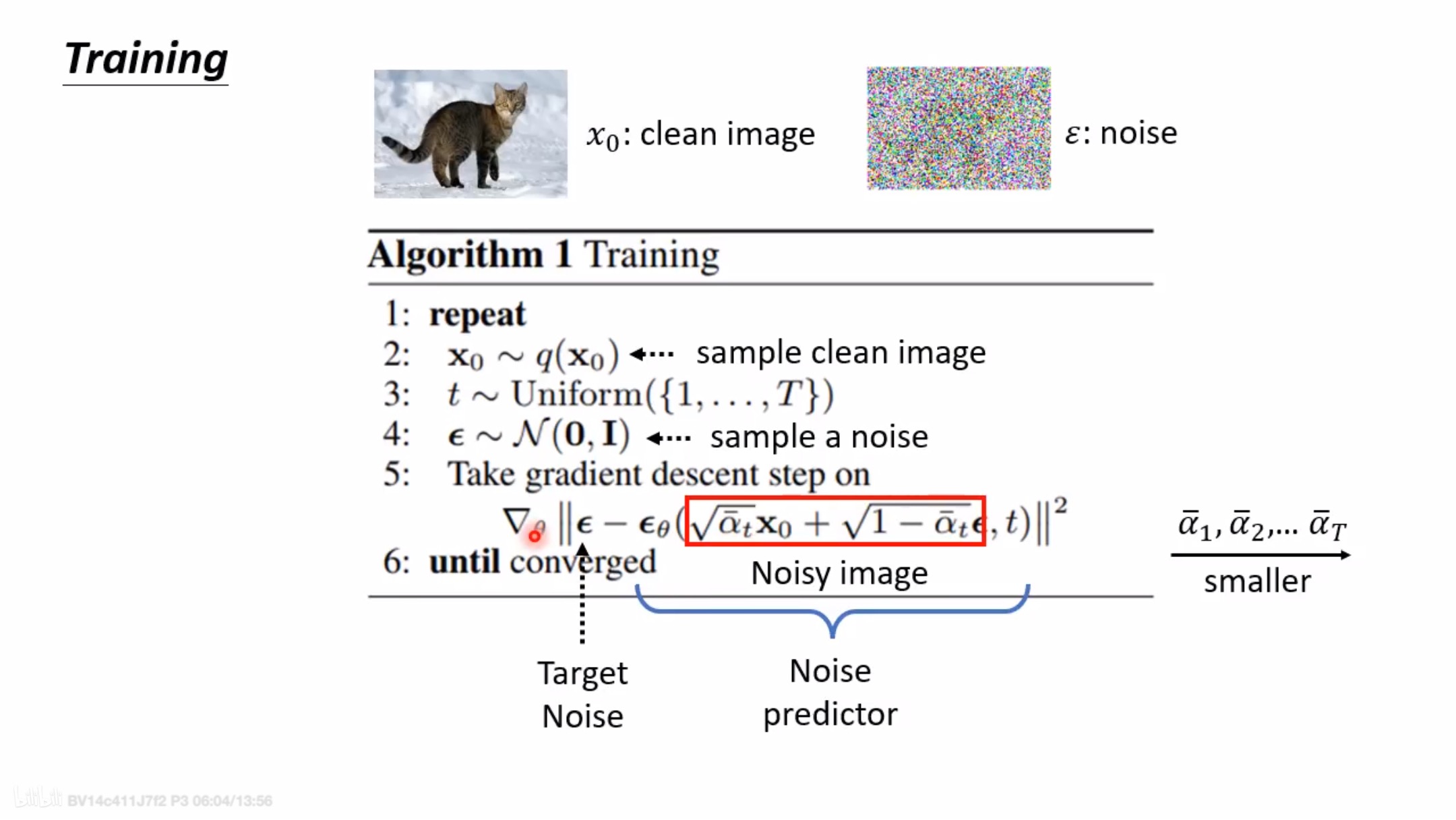
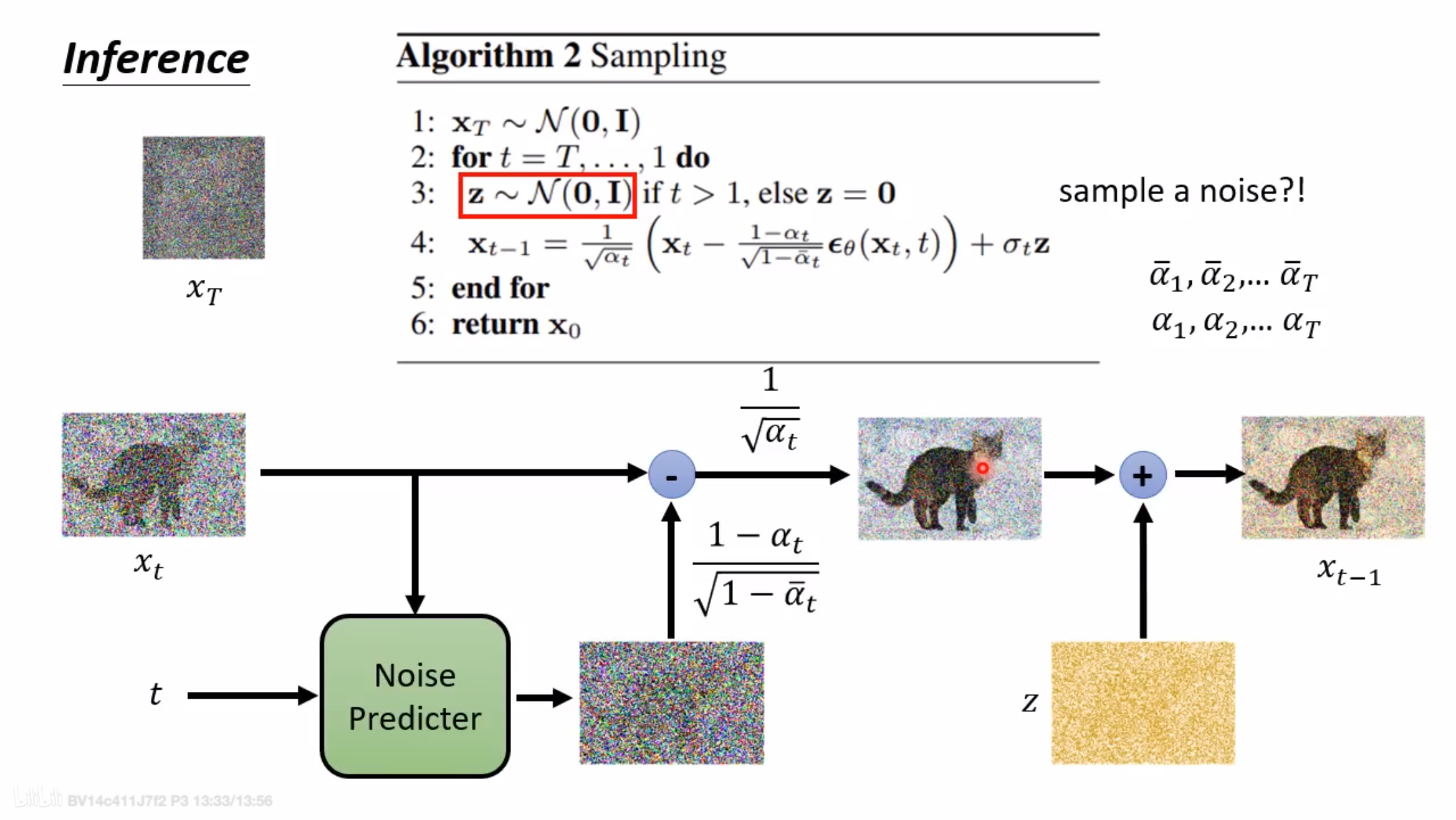
正向过程实现细节
正向过程其实就是一个不断加噪的过程,后一时刻的图像主要由两个量决定,其一是上一时刻图像,其二是所加噪声量。可以用一个公式来表示时刻和时刻两个图像的关系,如下:

其中,Xt表示t时刻的图像,Xt-1表示t-1时刻图像,Z1表示添加的高斯噪声,其服从N(0,1)分布。【注:N(0,1)表示标准高斯分布,其方差为1,均值为0】
其实,还和另外一个量有关:
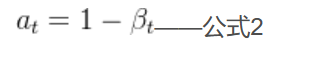
其中,是预先给定的值,它是一个随时刻不断增大的值,论文中它的范围为[0.0001,0.02]。既然
越来越大,则
越来越小,
越来越小,1−
越来越大。

公式4得到了什么——其得到了时刻图像和
时刻图像的关系。按照我们先前的理解,我们再列出
时刻图像和
时刻图像的关系,如下:

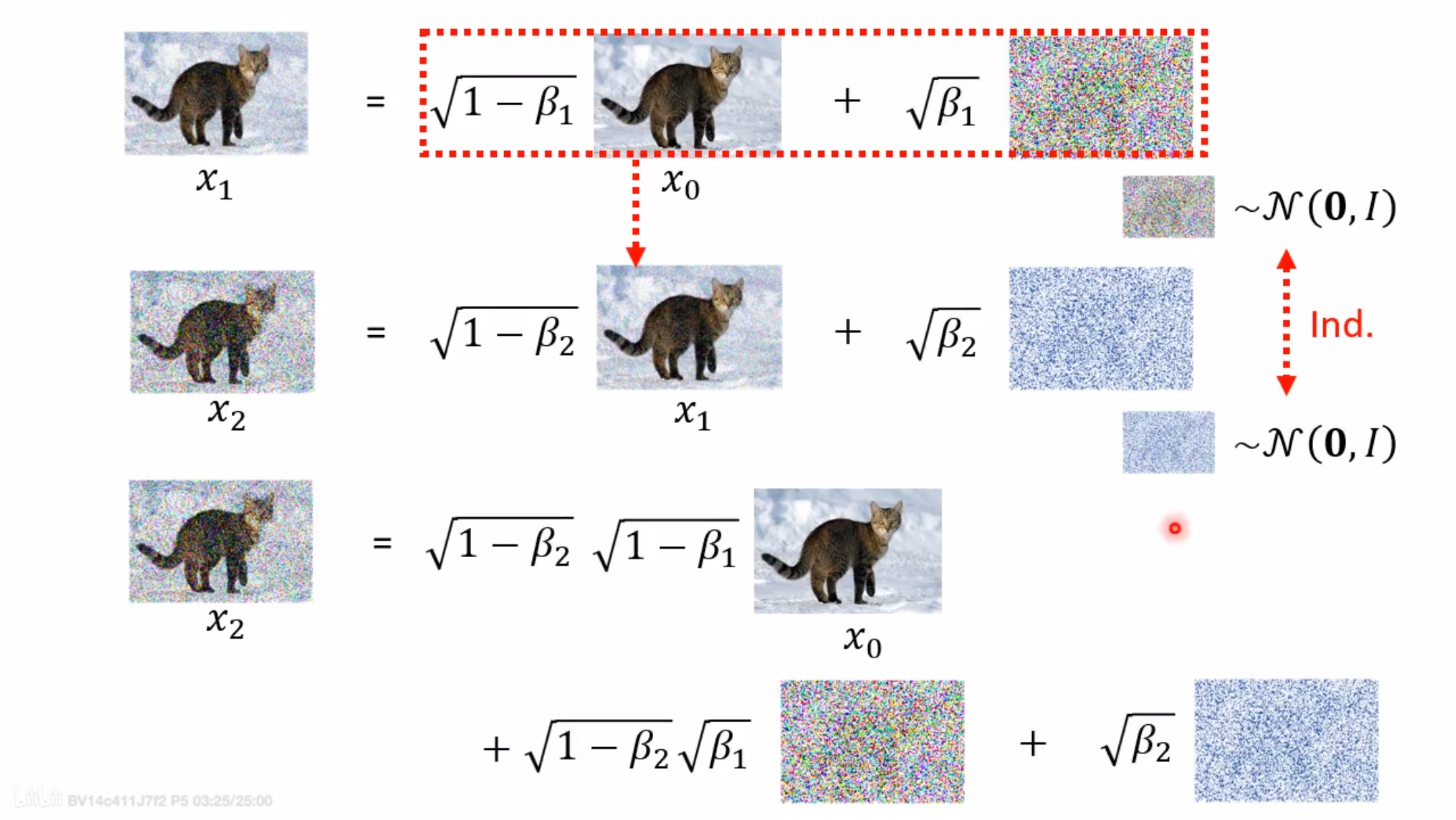

很明显的规律,这里我就根据这个规律直接写出 时刻图像和
时刻图像的关系,公式如下:

实际上就是,通过一次次的迭代太慢了,且每一次添加的噪声都独立且满足正态分布,正态分布相加还是正态分布,所以推导出了公式7
逆向过程实现细节
逆向过程是将高斯噪声还原为预期图片的过程。我们希望将时刻的高斯噪声变成时刻的图像,是很难一步到位的,因此我们思考能不能和正向过程一样,先考虑时刻图像和时刻的关系,然后一步步向前推导得出结论呢。
这里我们需要利用正向过程中的结论,我们在正向过程中可以由时刻图像得到 时刻图像,然后利用贝叶斯公式即可求解。贝叶斯公式的表达式如下:
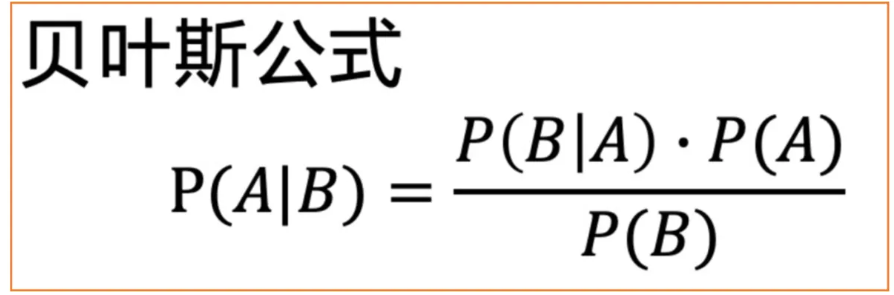
那么我们将利用贝叶斯公式来求时刻图像,公式如下:
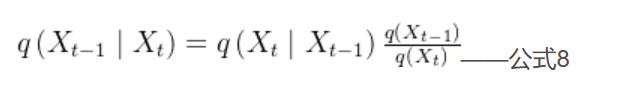
公式8中我们可以求得,就是刚刚正向过程求的嘛。 但
和
是未知的。又由公式7可知,可由
得到每一时刻的图像,那当然可以得到
和
时刻的图像,故将公式8加一个
作为已知条件,将公式8变成公式9,如下:
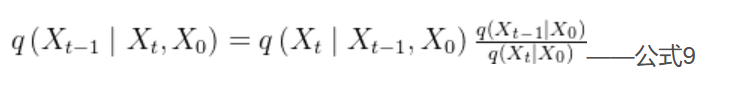
知道了公式9等式右边3项服从的分布,我们就可以计算出等式左边的。这个计算很简单,没有什么技巧,就是纯算。在附录->高斯分布性质部分我们知道了高斯分布的表达式为:
。那么我们只需要求出公式9等式右边3个高斯分布表达式,求出µ和σ,然后进行乘除运算即可求得
。
网络训练流程
我们最终要训练的实际上是一个噪声预测器。神经网络输出的噪声是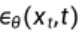 ,而真实的噪声取自于正态分布
,而真实的噪声取自于正态分布 ,则损失函数为:
,则损失函数为:
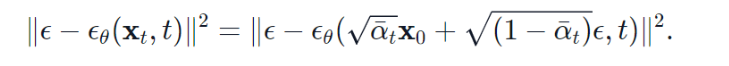
高斯分布性质
高斯分布又称正态分布,其表达式为:
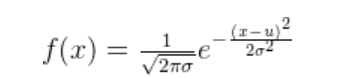
其中为均值,
为方差。若随机变量服
从正态均值为
,方差为
的高斯分布,一般记为
。此外,有一点大家需要知道,如果我们知道一个随机变量服从高斯分布,且知道他们的均值和方差,那么我们就能写出该随机变量的表达式。
高斯分布还有一些非常好的性质:
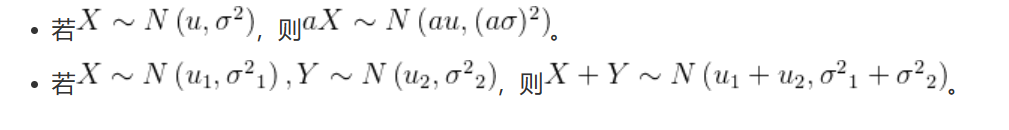
Diffusion Model扩散模型的更多相关文章
- 一文详解扩散模型:DDPM
作者:京东零售 刘岩 扩散模型讲解 前沿 人工智能生成内容(AI Generated Content,AIGC)近年来成为了非常前沿的一个研究方向,生成模型目前有四个流派,分别是生成对抗网络(Gene ...
- A Neural Influence Diffusion Model for Social Recommendation 笔记
目录 一.摘言 二.杂记 三.问题定义和一些准备工作 四.模型真思想 五.实验部分 六.参考文献 一.摘言 之前协同过滤利用user-item交互历史很好的表示了user和item.但是由于用户行为的 ...
- Hugging Face 每周速递: 扩散模型课程完成中文翻译,有个据说可以教 ChatGPT 看图的模型开源了
每一周,我们的同事都会向社区的成员们发布一些关于 Hugging Face 相关的更新,包括我们的产品和平台更新.社区活动.学习资源和内容更新.开源库和模型更新等,我们将其称之为「Hugging Ne ...
- Model Validation(模型验证)
Model Validation(模型验证) 前言 阅读本文之前,您也可以到Asp.Net Web API 2 系列导航进行查看 http://www.cnblogs.com/aehyok/p/344 ...
- 008.Adding a model to an ASP.NET Core MVC app --【在 asp.net core mvc 中添加一个model (模型)】
Adding a model to an ASP.NET Core MVC app在 asp.net core mvc 中添加一个model (模型)2017-3-30 8 分钟阅读时长 本文内容1. ...
- Box Model 盒子模型
Box Model盒子模型,是初学者在学习HTMl5时会学到的一个重要的模型,也有一些人称它为框模型,因为盒子是属于3维,而框是平面的.称之为盒子模型,是因为其结构和盒子十分相似,其最外面是margi ...
- Consistency Models终结扩散模型
最近看到一篇论文,觉得特别有意思,并且在学术界引起了不小的动静,他就是一致性模型,据说图像生成效果快.质量高,并且还可以实现零样本图像编辑,即不进行一些视觉任务训练,可以实现图像超分.修复.上色等功能 ...
- Maximum Entropy Model(最大熵模型)初理解
0,熵的描述 熵(entropy)指的是体系的混沌的程度(可也理解为一个随机变量的不确定性),它在控制论.概率论.数论.天体物理.生命科学等领域都有重要应用,在不同的学科中也有引申出的更为具体的定义, ...
- CSS Box Model 盒子模型
1. 介绍 1.1 什么是 Box Model 在HTML中的每个element(元素)都可以看作一个矩形的盒子,矩形从内到外依次由元素的内容(content).内边距(padding).边框(bor ...
- Keras Model Sequential模型接口
Sequential 模型 API 在阅读这片文档前,请先阅读 Keras Sequential 模型指引. Sequential 模型方法 compile compile(optimizer, lo ...
随机推荐
- 代替forever下一个部署node的持久化工具---pm2
最近有个后端项目,用的是node,在持久化的时候会挂掉,详细了解到用的是nohup,然后先详细了解了一下nohup nohup是一个Linux命令,用于在系统后台不挂断地运行命令,退出终端不会影响程序 ...
- BZ全景编辑器(KRPano全景可视化编辑器, 无需编写代码, 图形化制作全景漫游)
软件简介 BZ全景编辑器是一款KRPano全景可视化编辑工具,下载安装即可使用,无需拥有任何KRPano代码基础,便可以制作生成精美的全景漫游作品. BZ全景编辑器群:882083973 最新版软件下 ...
- Solution -「SP 106」BINSTIRL
Description Link. 求 \(\begin{Bmatrix}n \\ m\end{Bmatrix}\bmod2\) Solution 求 \[\begin{aligned} \begin ...
- Teamcenter RAC 开发之《日期控件》
背景 Teamcenter Rac 开发客制化表单过程中,发现一个问题,就是使用日期控件JXDatePicker展示无法实现"签出"禁用控件输入 解决办法 选择使用JDateCho ...
- Flask框架——详解URL、HTTP请求、视图函数和视图类
文章目录 1 什么是url? 2 为什么要有url? 3 如何应用url? 3.1 url和路由的区别. 3.2 url传参的两种 3.2.1动态路由传参 3.2.1.1 动态路由的过滤 3.2.2 ...
- 关于C++拷贝控制
通常来说,对于类内动态分配资源的类需要进行拷贝控制:要在拷贝构造函数.拷贝赋值运算符.析构函数中实现安全高效的操作来管理内存.但是资源管理并不是一个类需要定义自己的拷贝控制成员的唯一原因.C++ Pr ...
- 【RcoketMQ】RcoketMQ 5.0新特性(一)- Proxy
为了向云原生演进,提高资源利用和弹性能力,RcoketMQ在5.0进行了架构的调整与升级,先来看新特性之一,增加了Proxy层. 增加Proxy代理层 计算存储分离 计算存储分离是一种分层架构,将计算 ...
- 2020/5/8—cf,我裂开来
呜呜呜我爆零了呜呜呜ljll 嗯T1T2防爆零的没了呜呜呜在此纪念可怜的yjz大佬21发AC 太惨了(逃 先来说说我们都有些啥题目吧... T1 嗯,裂开了,当场裂开我一看!桶排!然后实现,嗯?嗯!嗯 ...
- 2D物理引擎 Box2D for javascript Games 第四章 将力作用到刚体上
2D物理引擎 Box2D for javascript Games 第四章 将力作用到刚体上 将力作用到刚体上 Box2D 是一个在力作用下的世界,它可以将力作用于刚体上,从而给我们一个更加真实的模拟 ...
- 随身wifi 救砖过程记录
7,8块钱买了个随身wifi,准备刷机玩的,后来不知道刷错了boot还是啥,加电后灯都不亮了,前期没备份,于是网上找了各种教程,下面记录下: 变砖后有个底层的9008驱动协议可以刷机,下面的过程都是基 ...
