启发式搜索（heuristic search）———A*算法

在宽度优先和深度优先搜索里面，我们都是根据搜索的顺序依次进行搜索，可以称为盲目搜索，搜索效率非常低。

而启发式搜索则大大提高了搜索效率，由这两张图可以看出它们的差别：

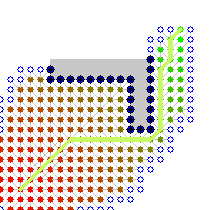（左图类似与盲搜，右图为启发式搜索）(图片来源)  

很明显启发式的搜索效率远远大于盲搜。

什么是启发式搜索（heuristic  search）

　　利用当前与问题有关的信息作为启发式信息，这些信息是能够提升查找效率以及减少查找次数的。

如何使用这些信息，我们定义了一个估价函数 h(x) 。h(x)是对当前状态x的一个估计，表示 x状态到目标状态的距离。

有：1、h(x) >= 0 ；  2、h(x)越小表示 x 越接近目标状态； 3、如果 h(x) ==0 ，说明达到目标状态。

与问题相关的启发式信息都被计算为一定的 h(x) 的值，引入到搜索过程中。

　　然而，有了启发式信息还不行，还需要起始状态到 x 状态所花的代价，我们称为 g(x) 。比如在走迷宫问题、八数码问题，我们的 g(x) 就是从起点到 x 位置花的步数 ，h(x) 就是与目标状态的曼哈顿距离或者相差的数目；在最短路径中，我们的 g(x) 就是到 x 点的权值，h(x)  就是 x 点到目标结点的最短路或直线距离。

　　现在，从 h(x) 和 g(x) 的定义中不能看出，假如我们搜索依据为 F(x) 函数。

　　当 F(x) = g(x) 的时候就是一个等代价搜索，完全是按照花了多少代价去搜索。比如 bfs，我们每次都是从离得近的层开始搜索，一层一层搜 ；以及dijkstra算法，也是依据每条边的代价开始选择搜索方向。

　　当F(x) = h(x) 的时候就相当于一个贪婪优先搜索。每次都是向最靠近目标的状态靠近。

　　人们发现，等代价搜索虽然具有完备性，能找到最优解，但是效率太低。贪婪优先搜索不具有完备性，不一定能找到解，最坏的情况下类似于dfs。

　　这时候，有人提出了A算法。令F(x) = g(x) + h(x) 。（这里的 h(x) 没有限制）。虽然提高了算法效率，但是不能保证找到最优解，不适合的 h(x)定义会导致算法找不到解。不具有完备性和最优性。

　　几年后有人提出了 A*算法。该算法仅仅对A算法进行了小小的修改。并证明了当估价函数满足一定条件，算法一定能找到最优解。估价函数满足一定条件的算法称为A*算法。

它的限制条件是 F(x) = g(x) + h(x) 。 代价函数g(x) >0 ；h(x) 的值不大于x到目标的实际代价 h*(x) 。即定义的 h(x) 是可纳的，是乐观的。

怎么理解第二个条件呢？

　　打个比方：你要从x走到目的地，那么 h(x) 就是你感觉或者目测大概要走的距离，h*(x) 则是你到达目的地后，发现你实际走了的距离。你预想的距离一定是比实际距离短，或者刚好等于实际距离的值。这样我们称你的 h(x) 是可纳的，是乐观的。

　不同的估价函数对算法的效率可能产生极大的影响。尤其是 h(x) 的选定，比如在接下来的八数码问题中，我们选择了曼哈顿距离之和作为 h(x) ，你也可以选择相差的格子作为 h(x)，只不过搜索的次数会不同。当 h(x) 越接近 h*(x) ，那么扩展的结点越少！

　 那么A*算法的具体实现是怎么样的呢？

1、将源点加入open表
2、
while(OPEN!=NULL)
{
    从OPEN表中取f(n)最小的节点n;
    if(n节点==目标节点)
        break;
    for(当前节点n的每个子节点X)
    {
        计算f(X);
        if(XinOPEN)
            if(新的f(X)<OPEN中的f(X))
            {
                把n设置为X的父亲;
                更新OPEN表中的f(n); //不要求记录路径的话可以直接加入open表，旧的X结点是不可能比新的先出队
            }
        if(XinCLOSE)
            continue;
        if(Xnotinboth)
        {
            把n设置为X的父亲;
            求f(X);
            并将X插入OPEN表中;
        }
    }//endfor
    将n节点插入CLOSE表中;
    按照f(n)将OPEN表中的节点排序;//实际上是比较OPEN表内节点f的大小，从最小路径的节点向下进行。
}//endwhile(OPEN!=NULL)

3、保存路径，从目标点出发，按照父节点指针遍历，直到找到起点。

以八数码问题为例：

我们从1、仅考虑代价函数； 2、仅考虑贪婪优先； 3、A*算法。

  1 #include<bits/stdc++.h>
  2 using namespace std;
  3 struct Maze{
  4     char s[3][3];
  5     int i,j,fx,gx;
  6     bool operator < (const Maze &a )const{
  7         return fx>a.fx;
  8     }
  9 } c;
 10 int fx[4][2]={{-1,0},{1,0},{0,1},{0,-1}};
 11 map<char ,Maze > mp;
 12 int T;
 13 int get_hx(char s[3][3]){
 14     int hx=0;
 15     for(int i=0;i<3;i++){
 16         for(int j=0;j<3;j++){
 17             hx+=abs(mp[s[i][j]].i-i)+abs(mp[s[i][j]].j-j);
 18         }
 19     }
 20     return (int)hx;
 21 }
 22 void pr(char s[3][3]){
 23     cout<<"step: "<<T++<<endl;
 24     for(int i=0;i<3;i++){
 25         for(int j=0;j<3;j++)
 26             cout<<s[i][j];
 27         cout<<endl;
 28     }
 29     cout<<endl;
 30 }
 31 int key(char s[3][3]){
 32     int ans=0;
 33     for(int i=0;i<3;i++)
 34         for(int j=0;j<3;j++)
 35             ans=ans*10+(s[i][j]-'0');
 36     return ans;
 37 }
 38 void BFS(){
 39     T=0;
 40     map<int ,bool >flag;
 41     queue < Maze > q;
 42     q.push(c);
 43     flag[key(c.s)]=1;
 44     while(!q.empty()){
 45         Maze now=q.front();
 46         q.pop();
 47         pr(now.s);
 48         if(get_hx(now.s)==0){
 49             break;
 50         }
 51         for(int i=0;i<4;i++){
 52             int x,y;
 53             x=now.i+fx[i][0];
 54             y=now.j+fx[i][1];
 55             if(!(x>=0&&x<3&&y>=0&&y<3)) continue;
 56             Maze tmp=now;
 57             tmp.s[now.i][now.j]=tmp.s[x][y];
 58             tmp.s[x][y]='0';
 59             tmp.i=x ; tmp.j=y ;
 60             tmp.fx++;
 61             if(!flag[key(tmp.s)]){
 62                 q.push(tmp);
 63                 flag[key(tmp.s)]=1;
 64             }
 65         }
 66     }
 67 }
 68 void Greedy_best_first_search(){
 69     T=0;
 70     priority_queue< Maze > q ;
 71     map<int ,int >flag;
 72     c.fx=get_hx(c.s);
 73     q.push(c);
 74     flag[key(c.s)]=1;
 75     while(!q.empty()){
 76         Maze now=q.top();
 77         q.pop();
 78         pr(now.s);
 79         if(get_hx(now.s)==0){
 80             break;
 81         }
 82         for(int i=0;i<4;i++){
 83             int x,y;
 84             x=now.i+fx[i][0];
 85             y=now.j+fx[i][1];
 86             if(!(x>=0&&x<3&&y>=0&&y<3)) continue;
 87             Maze tmp=now;
 88             tmp.s[now.i][now.j]=tmp.s[x][y];
 89             tmp.s[x][y]='0';
 90             tmp.i=x ; tmp.j=y ;
 91             tmp.fx=get_hx(tmp.s);
 92             if(!flag[key(tmp.s)]){
 93                 q.push(tmp);
 94                 flag[key(tmp.s)]=1;
 95             }
 96         }
 97     }
 98 }
 99 void A_star(){
100     T=0;
101     priority_queue< Maze > q ;
102     map<int ,int >flag;
103     c.gx=0;
104     c.fx=get_hx(c.s)+c.gx;
105     q.push(c);
106     while(!q.empty()){
107         Maze now=q.top();
108         q.pop();
109         flag[key(now.s)]=now.fx;
110         pr(now.s);
111         if(get_hx(now.s)==0){
112             break;
113         }
114         for(int i=0;i<4;i++){
115             int x,y;
116             x=now.i+fx[i][0];
117             y=now.j+fx[i][1];
118             if(!(x>=0&&x<3&&y>=0&&y<3)) continue;
119             Maze tmp=now;
120             tmp.s[now.i][now.j]=tmp.s[x][y];
121             tmp.s[x][y]='0';
122             tmp.i=x ; tmp.j=y ;
123             tmp.gx++;
124             tmp.fx=get_hx(tmp.s)+tmp.gx;
125             if(!flag[key(tmp.s)]){
126                 q.push(tmp);
127             }else if(flag[key(tmp.s)]>tmp.fx){
128                 flag[key(tmp.s)]=0;
129                 q.push(tmp);
130             }
131         }
132     }
133 }
134 int main(){
135     mp['1'].i=0;mp['1'].j=0;
136     mp['2'].i=0;mp['2'].j=1;
137     mp['3'].i=0;mp['3'].j=2;
138     mp['4'].i=1;mp['4'].j=2;
139     mp['5'].i=2;mp['5'].j=2;
140     mp['6'].i=2;mp['6'].j=1;
141     mp['7'].i=2;mp['7'].j=0;
142     mp['8'].i=1;mp['8'].j=0;
143     mp['0'].i=1;mp['0'].j=1;
144     for(int i=0;i<3;i++){
145         for(int j=0;j<3;j++){
146             cin>>c.s[i][j];
147         }
148         char x=getchar();
149     }
150     cin>>c.i>>c.j;
151     c.fx=0;
152     cout<<"八数码问题 BFS 解法(即仅以当前代价 g(x)搜索): "<<endl;
153     BFS();
154     cout<<"八数码问题 Greedy_best_first_search 解法(即仅以估计函数 h(x)搜索): "<<endl;
155     Greedy_best_first_search();
156     cout<<"八数码问题 A* 解法: "<<endl;
157     A_star();
158     return 0;
159 }
160 /*
161 283
162 164
163 705
164 2 1
165 */

结果显示：

1、仅考虑代价函数：36步。

2、仅考虑贪婪优先：5步。

3、A*算法：5步。

明显，在引入了启发式信息后，大大的提高了搜索的效率。

引申问题： 第 k 短路问题。

思路： 先从终点求出最短路，作为 h(x) 。然后维护优先队列，维护 F(x) 最小，第一次出来的终点是最短路，终点第二次出来的是次短路……

求第k短路时，A*算法优化的是查找的次数，可以理解为剪枝，更快速的找到最短路，次短路……
其他操作和正常的求最短路没有什么区别，找到终点第k次出队的值，就是第k短路。

（可能你会说在无向图中存在有回头路，没错，有可能次短路只是最短路走了一次回头路，但这确实也是一条次短路）。