noip2010 真题练习 2017.2.18

---

　　第一题比较简单，用exist数组判断是否在循环队列中，就可实现线性算法。

Code

 #include<iostream>
 #include<cstdio>
 #include<cctype>
 #include<cstring>
 #include<cstdlib>
 #include<fstream>
 #include<sstream>
 #include<algorithm>
 #include<map>
 #include<set>
 #include<queue>
 #include<vector>
 #include<stack>
 using namespace std;
 typedef bool boolean;
 #define INF 0xfffffff
 #define smin(a, b) a = min(a, b)
 #define smax(a, b) a = max(a, b)
 template<typename T>
 inline void readInteger(T& u){
     char x;
     int aFlag = ;
     while(!isdigit((x = getchar())) && x != '-');
     if(x == '-'){
         x = getchar();
         aFlag = -;
     }
     for(u = x - ''; isdigit((x = getchar())); u = (u << ) + (u << ) + x - '');
     ungetc(x, stdin);
     u *= aFlag;
 }

 int n, m;
 int top;
 int *s;
 boolean exist[];

 inline void s_push(int* sta, int x) {
     exist[sta[top] + ] = false;
     sta[top] = x;
     exist[x + ] = true;
     if(top == m - )    top = ;
     else top = top + ;
 }

 int res = ;
 inline void solve() {
     readInteger(m);
     readInteger(n);
     s = new int[(const int)(m + )];
     memset(s, -, sizeof(int) * (m + ));
     top = ;
     for(int i = , a; i <= n; i++) {
         readInteger(a);
         if(!exist[a + ]) {
             res++;
             s_push(s, a);
         }
     }
     printf("%d", res);
 }

 int main() {
     freopen("translate.in", "r", stdin);
     freopen("translate.out", "w", stdout);
     solve();
     return ;
 }

---

---

　　因为当卡牌的选择数是固定的情况下，跳的长度也就知道了，于是就可以用四种卡牌来做状态，得到了dp方程:

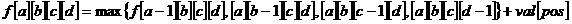
　　为了防止过多的无用的状态，所以就用记忆化搜索(其实直接4个for也没什么问题)

Code

 #include<iostream>
 #include<cstdio>
 #include<cctype>
 #include<cstring>
 #include<cstdlib>
 #include<fstream>
 #include<sstream>
 #include<algorithm>
 #include<map>
 #include<set>
 #include<queue>
 #include<vector>
 #include<stack>
 using namespace std;
 typedef bool boolean;
 #define INF 0xfffffff
 #define smin(a, b) a = min(a, b)
 #define smax(a, b) a = max(a, b)
 template<typename T>
 inline void readInteger(T& u){
     char x;
     int aFlag = ;
     while(!isdigit((x = getchar())) && x != '-');
     if(x == '-'){
         x = getchar();
         aFlag = -;
     }
     for(u = x - ''; isdigit((x = getchar())); u = (u << ) + (u << ) + x - '');
     ungetc(x, stdin);
     u *= aFlag;
 }

 int n, m;
 int counter[];
 int f[][][][];
 boolean vis[][][][];
 int *val;

 inline void init() {
     readInteger(n);
     readInteger(m);
     memset(counter, , sizeof(counter));
     memset(f, , sizeof(f));
     memset(vis, false, sizeof(vis));
     val = new int[(const int)(n + )];
     for(int i = ; i <= n; i++)        readInteger(val[i]);
     for(int i = , a; i <= m; i++) {
         readInteger(a);
         counter[a - ]++;
     }
     f[][][][] = val[];
     vis[][][][] = true;
 }

 int dfs(int a, int b, int c, int d) {
     if(vis[a][b][c][d])    return f[a][b][c][d];
     vis[a][b][c][d] = true;
     int pos = a *  + b *  + c *  + d *  + ;
     int ra = , rb = , rc = , rd = ;
     if(a > )    ra = dfs(a - , b, c, d);
     if(b > )    rb = dfs(a, b - , c, d);
     if(c > )    rc = dfs(a, b, c - , d);
     if(d > )    rd = dfs(a, b, c, d - );
     smax(f[a][b][c][d], max(ra, max(rb, max(rc, rd))) + val[pos]);
     return f[a][b][c][d];
 }

 inline void solve() {
     int res = dfs(counter[], counter[], counter[], counter[]);
     printf("%d", res);
 }

 int main() {
     freopen("tortoise.in", "r", stdin);
     freopen("tortoise.out", "w", stdout);
     init();
     solve();
     return ;
 }

---

---

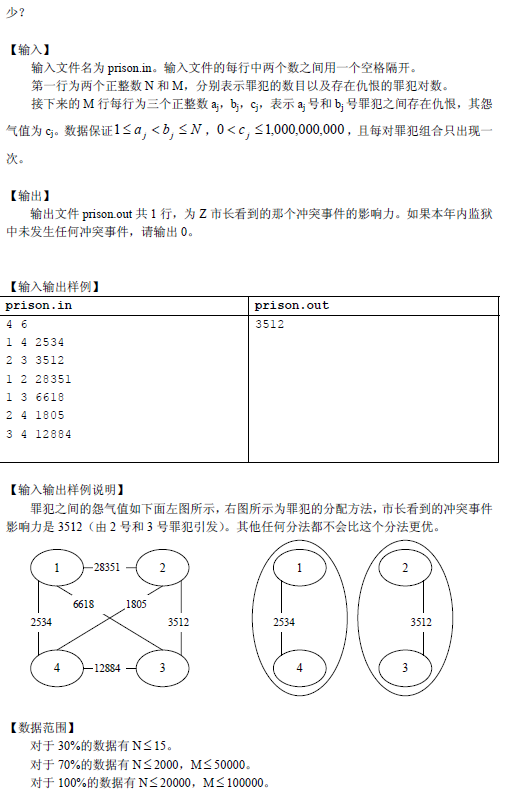
　　这道题相当于是安排罪犯，使所有的影响力的最大值最小，于是就不难想到二分答案。

　　对于当前二分值mid，无视所有权值小于等于它的边，判断是否能让剩下的边构成二分图。至于这一步多次对未访问的点进行dfs，将与它相连的点丢进另一个监狱，如果出现矛盾，就说明当前的二分值不合法。

Code

 #include<iostream>
 #include<cstdio>
 #include<cctype>
 #include<cstring>
 #include<cstdlib>
 #include<fstream>
 #include<sstream>
 #include<algorithm>
 #include<map>
 #include<set>
 #include<queue>
 #include<vector>
 #include<stack>
 using namespace std;
 typedef bool boolean;
 #define INF 0xfffffff
 #define smin(a, b) a = min(a, b)
 #define smax(a, b) a = max(a, b)
 template<typename T>
 inline void readInteger(T& u){
     char x;
     int aFlag = ;
     while(!isdigit((x = getchar())) && x != '-');
     if(x == '-'){
         x = getchar();
         aFlag = -;
     }
     for(u = x - ''; isdigit((x = getchar())); u = (u << ) + (u << ) + x - '');
     ungetc(x, stdin);
     u *= aFlag;
 }

 typedef class Edge {
     public:
         int end;
         int next;
         int w;
         Edge(const int end = , const int next = , const int w = ):end(end), next(next), w(w) {        }
 }Edge;

 typedef class MapManager{
     public:
         int ce;
         int *h;
         Edge *edge;
         MapManager(){}
         MapManager(int points, int limit):ce(){
             h = new int[(const int)(points + )];
             edge = new Edge[(const int)(limit + )];
             memset(h, , sizeof(int) * (points + ));
         }
         inline void addEdge(int from, int end, int w){
             edge[++ce] = Edge(end, h[from], w);
             h[from] = ce;
         }
         inline void addDoubleEdge(int from, int end, int w){
             addEdge(from, end, w);
             addEdge(end, from, w);
         }
         Edge& operator [](int pos) {
             return edge[pos];
         }
 }MapManager;
 #define m_begin(g, i) (g).h[(i)]

 int n, m;
 MapManager g;
 int* belong;
 int maxval = -;

 inline void init() {
     readInteger(n);
     readInteger(m);
     g = MapManager(n,  * m);
     belong = new int[(const int)(n + )];
     for(int i = , a, b, w; i <= m; i++) {
         readInteger(a);
         readInteger(b);
         readInteger(w);
         g.addDoubleEdge(a, b, w);
         smax(maxval, w);
     }
 }

 boolean dfs(int node, int val, int x) {
     if(belong[node] != -)    return belong[node] == val;
     else    belong[node] = val;
     for(int i = m_begin(g, node); i != ; i = g[i].next) {
         if(g[i].w <= x)    continue;
         int& e = g[i].end;
         if(!dfs(e, val ^ , x))    return false;
     }
     return true;
 }

 boolean check(int x) {
     memset(belong, -, sizeof(int) * (n + ));
     for(int i = ; i <= n; i++) {
         if(belong[i] == -)
             if(!dfs(i, , x))    return false;
     }
     return true;
 }

 inline void solve() {
     int l = , r = maxval;
     while(l <= r) {
         int mid = (l + r) >> ;
         if(!check(mid))    l = mid + ;
         else r = mid - ;
     }
     printf("%d", r + );
 }

 int main() {
     freopen("prison.in", "r", stdin);
     freopen("prison.out", "w", stdout);
     init();
     solve();
     return ;
 }

---

---

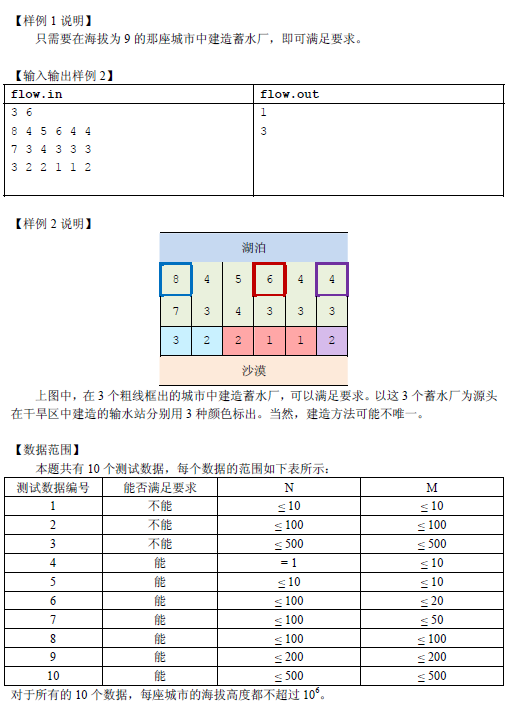
　　对于可以使干旱区的每个城市都能够获得水的情况，那么对于湖泊边的某个城市建的蓄水厂，能够提供给干旱区的城市水的集合，是一段连续的区间。这里可以简要地说明一下

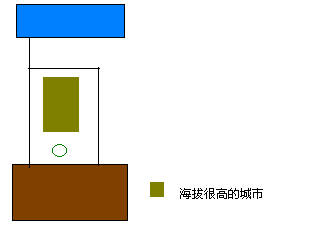
　　假设上面的命题不成立，就会出现形如上面的情况，那么为了使中间的小圆圈所在的城市可以得到供水，那么一定会有其他的水路和这几条水路交叉，也就是说这个蓄水厂还是可以给小圆圈所在的城市供水，矛盾，所以上面的命题成立。

　　于是我们可以通过M次dfs得到假设在第一行第i个城市建蓄水厂所能够供水的区间，当然这样的时间复杂度最极端的情况下是O(m²n)。但是仔细一想,对于一个点(i,j)它可以到达的干旱区城市，那么某个可以到达它的点(i+a,j+b)一定也可以到达它所可以到达的干旱区城市，于是只需要一些dfs从没有被访问的第一行的城市开始搜索，因为每个城市只会被访问一次，所以时间复杂度为O(mn)，降回了可以接受的范围。

　　得到了这么一堆区间可以干什么?我们是需要选择一些区间使得它们的并集是整个干旱区，于是可以用dp[i]来表示完全覆盖干旱区第1个城市到第j个城市的最小所需的区间，于是又得到了方程:

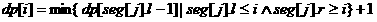
Code

 #include<iostream>
 #include<cstdio>
 #include<cctype>
 #include<cstring>
 #include<cstdlib>
 #include<fstream>
 #include<sstream>
 #include<algorithm>
 #include<map>
 #include<set>
 #include<queue>
 #include<vector>
 #include<stack>
 using namespace std;
 typedef bool boolean;
 #define INF 0xfffffff
 #define smin(a, b) a = min(a, b)
 #define smax(a, b) a = max(a, b)
 template<typename T>
 inline void readInteger(T& u){
     char x;
     int aFlag = ;
     while(!isdigit((x = getchar())) && x != '-');
     if(x == '-'){
         x = getchar();
         aFlag = -;
     }
     for(u = x - ''; isdigit((x = getchar())); u = (u << ) + (u << ) + x - '');
     ungetc(x, stdin);
     u *= aFlag;
 }

 typedef class Point {
     public:
         int x, y;
         int l, r;

         Point(const int x = , const int y = , const int l = , const int r = ):x(x), y(y), l(l), r(r) {        }

         boolean mergable(Point& b) {
             if(b.l < l)    return true;
             if(b.r > r)    return true;
             return false;
         }
         void merge(Point& b) {
             smin(l, b.l);
             smax(r, b.r);
         }
 }Point;

 int n, m;
 int mat[][];

 inline void init() {
     readInteger(n);
     readInteger(m);
     for(int i = ; i <= n; i++) {
         for(int j = ; j <= m; j++) {
             readInteger(mat[i][j]);
         }
     }
 }

 const int mover[][] = {{, , , -}, {, , -, }};

 Point f[][];
 boolean vis[][];
 Point dfs(int x, int y) {
     if(vis[x][y])    return f[x][y];
     vis[x][y] = true;
     f[x][y] = Point(x, y, , );
     if(x == n)    f[x][y] = Point(x, y, y, y);
     for(int k = ; k < ; k++) {
         int x1 = x + mover[][k], y1 = y + mover[][k];
         if(x1 <  || x1 > n)    continue;
         if(y1 <  || y1 > m)    continue;
         if(mat[x1][y1] < mat[x][y]) {
             Point e = dfs(x1, y1);
             f[x][y].merge(e);
         }
     }
     return f[x][y];
 }

 void dfs1(int x, int y) {
     if(vis[x][y])    return;
     vis[x][y] = true;
     for(int k = ; k < ; k++) {
         int x1 = x + mover[][k], y1 = y + mover[][k];
         if(x1 <  || x1 > n)    continue;
         if(y1 <  || y1 > m)    continue;
         if(mat[x1][y1] < mat[x][y]) {
             Point e = dfs(x1, y1);
             f[x][y].merge(e);
         }
     }
 }

 int *dp;
 inline void solve() {
     memset(vis, false, sizeof(vis));
     for(int i = ; i <= m; i++)
         if(!vis[][i])
             dfs(, i);
     dp = new int[(const int)(m + )];
     memset(dp, , sizeof(int) * (m + ));
     for(int i = ; i <= m; i++)
         if(f[][i].l < )
             dp[f[][i].l] += , dp[f[][i].r + ] -= ;
     int unget = ;
     for(int i = ; i <= m; i++) {
         if(!vis[n][i])
             unget++;
     }
     if(unget > ) {
         printf("0\n%d", unget);
         return;
     }
     memset(dp, 0x7f, sizeof(int) * (m + ));
     dp[] = ;
     for(int i = ; i <= m; i++) {
         for(int j = ; j <= m; j++) {
             if(f[][j].l > i || f[][j].r < i)    continue;
             smin(dp[i], dp[f[][j].l - ] + );
         }
     }
     printf("1\n%d", dp[m]);
 }

 int main() {
     freopen("flow.in", "r", stdin);
     freopen("flow.out", "w", stdout);
     init();
     solve();
     return ;
 }