OpenCV 学习笔记03 凸包convexHull、道格拉斯-普克算法Douglas-Peucker algorithm、approxPloyDP 函数

凸形状内部的任意两点的连线都应该在形状里面。

1 道格拉斯-普克算法 Douglas-Peucker algorithm

这个算法在其他文章中讲述的非常详细，此处就详细撰述。

下图是引用维基百科的。ε称之为阈值 shreshold

图一

静态图如下：

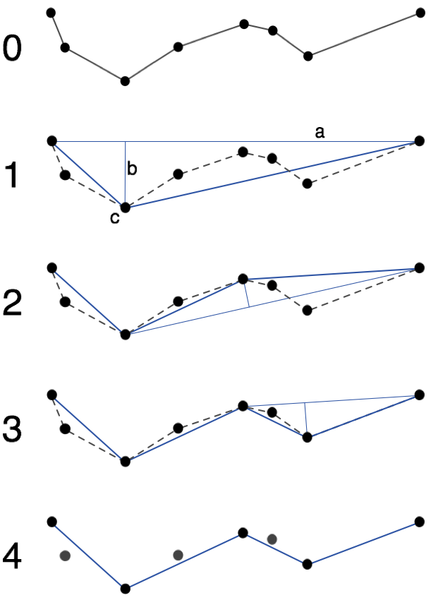
具体详细的可以参考如下两篇文章。

相关文章如下：

道格拉斯-普克 抽稀算法 附javascript实现，该文章只看他的文字讲解就好，他的代码不是通过python实现的。

道格拉斯-普克算法（Douglas–Peucker algorithm），该文章讲的也比较详细。

Ramer-Douglas-Peucker算法，维基百科的名词诠释

2 实现函数 cv2.approxPloyDP

作用：对目标图像进行（按指定精度、阈值，两者是一个概念）进行近似多边形曲线拟合。

使用一个较少顶点的曲线/多边形去拟合一个顶点较多的曲线/多边形，两曲线/多边形间的距离小于或等于某一指定精度/阈值

cv2.approxPolyDP(curve, epsilon, closed) -> approxCurve

参数：

curve - 2D点矢量，为图像的 “ 轮廓 ” 值。

epsilon - 指定近似精度的参数ε，这是原始曲线与其近似值之间的最大距离。参数越小，两直线越接近

closed - 若为true，曲线第一个点与最后一个点连接形成闭合曲线，若为false，曲线不闭合。

返回值：

approxCurve - 曲线/多边形近似结果。

备注：

为什么已经有了一个能够精确表示的轮廓 2D点矢量，却还需要得到一个近似多边形呢？

这主要是近似得到的多边形是由一组直线构成的，故能够在一个区域内定义多边形，以便后续的操作和处理，该项操作在许多计算机视觉任务中非常重要。

代码示例：

# epsilon 为近似度参数，该值需要轮廓的周长信息
# 多边形周长与源轮廓周长之比就是epsilon
epsilon = 0.01 * cv2.arcLength(cnt,True)
approx = cv2.approxPolyDP(cnt, epsilon, True)

# approx 为列表list，若approx为元组，则需要将其转换成列表list
# 为了安全起见，可将[approx]作为参数传入函数
cv2.drawContours(img, [approx], -1, (255, 255, 0), 2)

运行：

当 epsilon 的取值不同时，会存在不同的拟合程度。

3 凸包convexHull

作用：找到2D点集的凸包

cv2.convexHull(points[, clockwise[, returnPoints]]]) -> hull

参数：

points - 2D点集 2D point set

clockwise - 布尔类型，默认false；若为true，输出的凸包则为顺时针方向；若为false，输出的凸包则为逆时针方向。注意：这里的坐标系是x轴方向指向右侧，y轴方向指向上方。

returnPoints - 布尔类型，默认true，在矩阵情况下，若为true，则返回凸包点集；若为false，则返回整数向量的索引

返回值：

hull - 输出的凸包，是整数向量的索引（an integer vector of indices）或点集向量（vector of points）

代码示例：

hull = cv2.convexHull(cnt)

运行：

4 代码综合

4.1 保留原始图像

将上述代码进行综合，示例如下

import cv2
import numpy as np

img = cv2.imread('Mjolnir.jpg')
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
ret, binary = cv2.threshold(gray,127,255,cv2.THRESH_BINARY)
contours, hierarchy = cv2.findContours(binary,cv2.RETR_EXTERNAL,cv2.CHAIN_APPROX_SIMPLE) 

for cnt in contours:

    # ----源轮廓-------
    cv2.drawContours(img, [cnt], -1, (0, 255, 0), 2)

    # 近似多边形
    # epsilon 为近似度参数，该值需要轮廓的周长信息
    # 多边形周长与源轮廓周长之比就是epsilon
    epsilon = 0.01 * cv2.arcLength(cnt,True)
    approx = cv2.approxPolyDP(cnt, epsilon, True)
    cv2.drawContours(img, [approx], -1, (255, 255, 0), 2)

    # 凸包
    hull = cv2.convexHull(cnt)
    cv2.drawContours(img, [hull], -1, (0, 0, 255), 2)

cv2.imshow("approx",img)
cv2.waitKey(0)
cv2.destroyAllWindows()

运行

4.2 在新建幕布上绘制轮廓

当然在书（OpenCV 3 计算机视觉）第三章 3.10 凸轮廓与Douglas-Peucker算法 中，是将三个轮廓放在了黑色图像上。

实现代码如下：

import cv2
import numpy as np

img = cv2.imread('Mjolnir.jpg')
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
ret, binary = cv2.threshold(gray,127,255,cv2.THRESH_BINARY)
contours, hierarchy = cv2.findContours(binary,cv2.RETR_EXTERNAL,cv2.CHAIN_APPROX_SIMPLE)
# 生成黑色"幕布"
black = cv2.cvtColor(np.zeros((img.shape[1], img.shape[0]), dtype=np.uint8), cv2.COLOR_GRAY2BGR)

for cnt in contours:

    # ----源轮廓-------
    cv2.drawContours(black, [cnt], -1, (0, 255, 0), 2)

    # 近似多边形
    # epsilon 为近似度参数，该值需要轮廓的周长信息
    # 多边形周长与源轮廓周长之比就是epsilon
    epsilon = 0.01 * cv2.arcLength(cnt,True)
    approx = cv2.approxPolyDP(cnt, epsilon, True)
    cv2.drawContours(black, [approx], -1, (255, 255, 0), 2)

    # 凸包
    hull = cv2.convexHull(cnt)
    cv2.drawContours(black, [hull], -1, (0, 0, 255), 2)

cv2.imshow("approx",black)
cv2.waitKey(0)
cv2.destroyAllWindows()

运行

参考：

OpenCV入门之寻找图像的凸包（convex hull）关于凸包，讲的不错。

Convex Hull在Python和C ++中使用OpenCV 讲解的非常详细以及每一步的实现语言

opencv学习(四十一)之寻找凸包convexHull() 虽然实现语言不同，但是讲解还挺详细的

Convex Hull 这个粉红色的，是不是萌妹版

边缘检测，框出物体的轮廓(使用opencv-python)

Python+OpenCV教程番外篇9：凸包及更多轮廓特征

结构分析和形状描述符 官方文档

opencv-python的中文教程 - OpenCV中的轮廓 较为系统性

Convex Hull在Python和C ++中使用OpenCV  较为系统性

代码图像素材：