[hihoCoder] 第五十周: 欧拉路·二

题目1 : 欧拉路·二

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

在上一回中小Hi和小Ho控制着主角收集了分散在各个木桥上的道具，这些道具其实是一块一块骨牌。

主角继续往前走，面前出现了一座石桥，石桥的尽头有一道火焰墙，似乎无法通过。

小Hi注意到在桥头有一张小纸片，于是控制主角捡起了这张纸片，只见上面写着：

将M块骨牌首尾相连放置于石桥的凹糟中，即可关闭火焰墙。切记骨牌需要数字相同才能连接。
——By 无名的冒险者

小Hi和小Ho打开了主角的道具栏，发现主角恰好拥有M快骨牌。

小Ho：也就是说要把所有骨牌都放在凹槽中才能关闭火焰墙，数字相同是什么意思？

小Hi：你看，每一块骨牌两端各有一个数字，大概是只有当数字相同时才可以相连放置，比如：

小Ho：原来如此，那么我们先看看能不能把所有的骨牌连接起来吧。

提示：Fleury算法求欧拉路径

输入

第1行：2个正整数，N,M。分别表示骨牌上出现的最大数字和骨牌数量。1≤N≤1,000，1≤M≤5,000

第2..M+1行：每行2个整数，u,v。第i+1行表示第i块骨牌两端的数字(u,v)，1≤u,v≤N

输出

第1行：m+1个数字，表示骨牌首尾相连后的数字

比如骨牌连接的状态为(1,5)(5,3)(3,2)(2,4)(4,3)，则输出"1 5 3 2 4 3"

你可以输出任意一组合法的解。

样例输入

5 5
3 5
3 2
4 2
3 4
5 1

样例输出

1 5 3 4 2 3

小Ho：这种简单的谜题就交给我吧！

小Hi：真的没问题么？

<10分钟过去>

小Ho：啊啊啊啊啊！搞不定啊！！！骨牌数量一多就乱了。

小Hi：哎，我就知道你会遇到问题。

小Ho：小Hi快来帮帮我！

小Hi：好了，好了。让我们一起来解决这个问题。

<小Hi思考了一下>

小Hi：原来是这样。。。小Ho你仔细观察这个例子：

因为相连的两个数字总是相同的，不妨我们只写一次，那么这个例子可以写成：3-2-4-3-5-1。6个数字刚好有5个间隙，每个间隙两边的数字由恰好对应了一块骨牌。

如果我们将每一个数字看作一个点，每一块骨牌看作一条边。你觉得是怎么样的呢？

小Ho：以这个例子来说的话，就是：

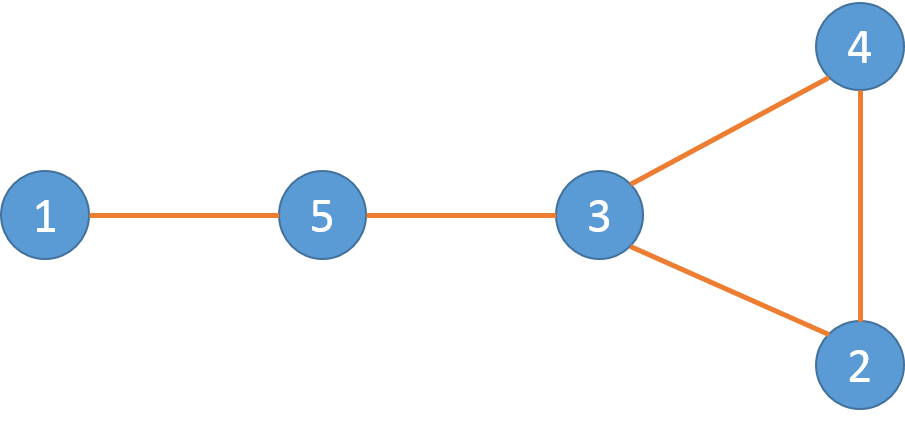
要把所有的骨牌连起来，也就是把所有的边都走一次。咦，这不是欧拉路问题么！

小Hi：没错，这问题其实就是一个欧拉路的问题，不过和上一次不一样的在于，这一次我们要找出一条欧拉路径。

小Ho：那我们应该如何来找一条路径呢？

小Hi：我们还是借用一下上次的例子吧

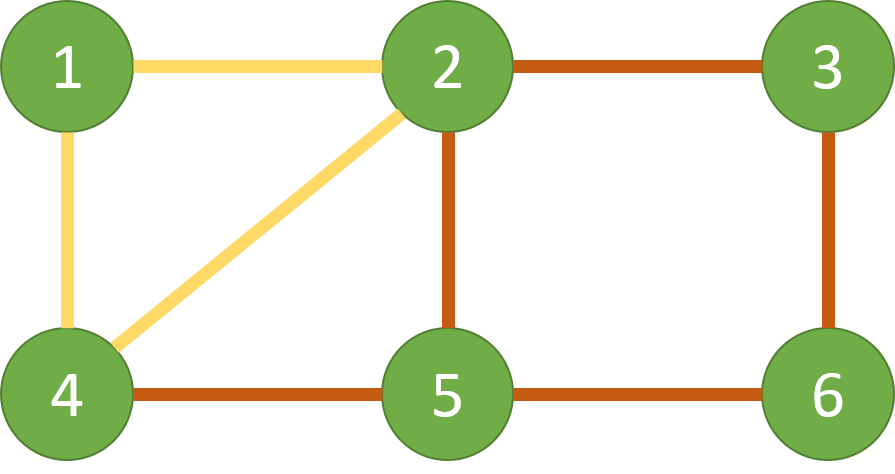
使用我们上一次证明欧拉路判定的方法，我们在这个例子中找到了2条路径：

L1: 4-5-2-3-6-5
L2: 2-4-1-2

假设我们栈S，记录我们每一次查找路径时的结点顺序。当我们找到L1时，栈S内的情况为：

S: 4 5 2 3 6 5 [Top]

此时我们一步一步出栈并将这些边删除。当我们到节点2时，我们发现节点2刚好是L1与L2的公共节点。并且L2满足走过其他边之后回到了节点2。如果我们在这个地方将L2先走一遍，再继续走L1不就刚好走过了所有边么。

而且在上一次的证明中我们知道，除了L1之外，其他的路径L2、L3...一定都满足起点与终点为同一个点。所以从任意一个公共节点出发一定有一条路径回到这个节点。

由此我们得到了一个算法：

1. 在原图中找一个L1路径

2. 从L1的终点往回回溯，依次将每个点出栈。并检查当前点是否还有其他没有经过的边。若存在则以当前点为起点，查找L2，并对L2的节点同样用栈记录重复该算法。

3. 当L1中的点全部出栈后，算法结束。

在这里我们再来一个有3层的例子：

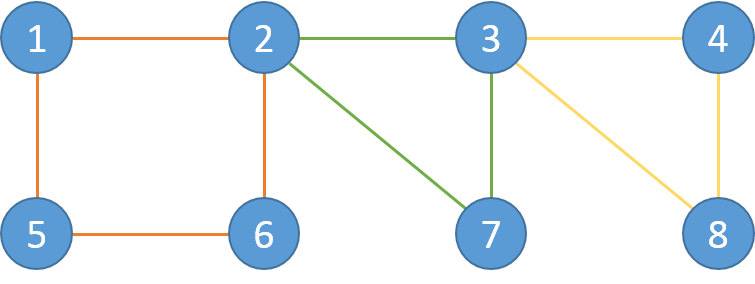
在这个例子中：

L1: 1-2-6-5-1
L2: 2-3-7-2
L3: 3-4-8-3

第一步时我们将L1压入栈S，同时我们用一个数组Path来记录我们出栈的顺序：

S: [1 2 6 5 1]
Path:

然后出栈到节点2时我们发现了2有其他路径，于是我们把2的另一条路径加入：

S: 1 [2 3 7 2]
Path: 1 5 6

此时L2已经走完，然后再开始弹出元素，直到我们发现3有其他路径，同样压入栈：

S: 1 2 [3 4 8 3]
Path: 1 5 6 2 7

之后依次弹出剩下的元素：

S:
Path: 1 5 6 2 7 3 8 4 3 2 1

此时的Path就正好是我们需要的欧拉路径。

小Ho：原来这样就能求出欧拉路，真是挺巧妙的。

小Hi：而且这个算法在实现时也有很巧妙的方法。因为DFS本身就是一个入栈出栈的过程，所以我们直接利用DFS的性质来实现栈，其伪代码如下：

DFS(u):
	While (u存在未被删除的边e(u,v))
		删除边e(u,v)
		DFS(v)
	End
	PathSize ← PathSize + 1
	Path[ PathSize ] ← u

小Ho：这代码好简单，我觉得我可以实现它！

小Hi：那么实现就交给你了

小Ho：没问题！交给我吧

 

 #include <bits/stdc++.h>
 using namespace std;

 int N, M;
 int u, v;
 vector<vector<int>> graph;
 vector<int> inDegree;
 vector<int> path;

 void dfs(int u) {
     for (int v = ; v <= N; ++v) {
         if (graph[v][u] == ) continue;
         --graph[v][u];
         --graph[u][v];
         dfs(v);
     }
     path.push_back(u);
 }

 int main() {
     while (cin >> N >> M) {
         graph.assign(N + , vector<int>(N + , ));
         inDegree.assign(N + , );
         path.clear();
         for (int i = ; i < M; ++i) {
             cin >> u >> v;
             ++graph[u][v];
             ++graph[v][u];
             ++inDegree[v];
             ++inDegree[u];
         }
         int start = ;
         for (int i = ; i <= N; ++i) if (inDegree[i] & ) {
             start = i;
             break;
         }
         dfs(start);
         for (int i = ; i < path.size(); ++i) {
             cout << path[i] << " ";
         }
         cout << endl;
     }
     return ;
 }