自适应滤波：维纳滤波器——LCMV及MVDR实现

作者：桂。

时间：2017-03-24  06:52:36

链接：http://www.cnblogs.com/xingshansi/p/6609317.html

声明：欢迎被转载，不过记得注明出处哦~

---

【读书笔记03】

前言

西蒙.赫金的《自适应滤波器原理》第四版，上一篇看到维纳滤波基本形式：最优化问题，且无任何条件约束。这次看到有约束的部分，简单整理一下思路：

　　1）拉格朗日乘子法；

　　2）线性约束最小方差滤波器（Linearly constrained minimum-variance，LCMV）;

　　3）谱估计之MVDR算法（Minimum variance distortionless response ，MVDR）；

内容为自己的学习总结，如有错误之处，还请各位帮忙指出！

一、拉格朗日乘子法

学习到含有约束条件的Wiener Filter，拉格朗日乘子法是解决：将含约束条件的优化问题转化为无约束条件优化问题的途径，故先梳理一下。

　　A-只含一个等式约束的最优化

实函数$f\left( {\bf{w}} \right)$是参数向量${\bf{w}}$的二次函数，约束条件是：

${{{\bf{w}}^H}{\bf{s}} = g}$

其中$\bf{s}$是已知向量，$g$是复常数。例如在波束形成应用中${\bf{w}}$表示各传感器输出的一组复数权值，$\bf{s}$是一个旋转向量。假设该问题是一个最小化问题，令$c\left( {\bf{w}} \right) = {{\bf{w}}^H}{\bf{s}} - g = 0 + j0$可以描述为：

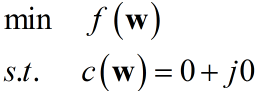
所谓拉格朗日乘子法，就是引入拉格朗日乘子：将上述约束最小化问题转化为无约束问题，定义一个新的实函数：

$h\left( {\bf{w}} \right) = f\left( {\bf{w}} \right) + {\lambda _1}{\mathop{\rm Re}\nolimits} \left[ {c\left( {\bf{w}} \right)} \right] + {\lambda _2}{\mathop{\rm Im}\nolimits} \left[ {c\left( {\bf{w}} \right)} \right]$

现在定义一个复拉格朗日乘子：

$\lambda  = {\lambda _1} + {\lambda _2}$

$h({\bf{w}})$改写为：

$h\left( {\bf{w}} \right) = f\left( {\bf{w}} \right) + {\mathop{\rm Re}\nolimits} \left[ {{\lambda ^*}c\left( {\bf{w}} \right)} \right]$

至此，无约束优化问题转化完成，利用偏导求参即可，其实这是一个简化的形式，分别求解$\lambda _1$、$\lambda _2$也是一样的。

　　B-包含多个等式约束的最优化

实函数$f\left( {\bf{w}} \right)$是参数向量${\bf{w}}$的二次函数，约束条件是：

${{{\bf{w}}^H}{\bf{s_k}} = g_k}$

其中$k = 1,2...K$，方法同单个约束情况相同，求解伴随方程：

$\frac{{\partial f}}{{\partial {{\bf{w}}^*}}} + \sum\limits_{k = 1}^K {\frac{\partial }{{\partial {{\bf{w}}^*}}}\left( {{\mathop{\rm Re}\nolimits} \left[ {\lambda _k^*{c_k}\left( {\bf{w}} \right)} \right]} \right)}  = {\bf{0}}$

此时与多个等式约束联合成方程组，这个方程组定义了${\bf{w}}$和拉格朗日乘子${\lambda _1}$、${\lambda _2}$...${\lambda _K}$的解。

二、线性约束最小方差滤波器

　　之前看到的维纳滤波都是基于最小均方误差准则，而没有添加任何约束，此处考虑含有线性约束情况下的方差滤波器，文中给了一个图：

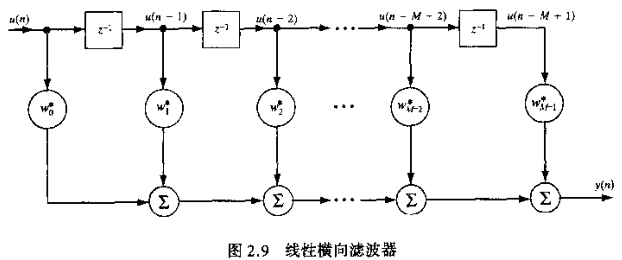
其中$x(n)$为输入信号(即$u$，为了与下文统一，用$x$表示)，$w_i$为权重，$y(n)$为滤波器输出：

$y\left( n \right) = \sum\limits_{k = 0}^{M - 1} {{w^*_k}x\left( {n - k} \right)} $

这个优化问题如果没有约束可以表述为：

$\arg \mathop {\min }\limits_{\bf{w}} J = E\left[ {{y^H}y} \right]$

假设$\theta_0$为目标达到角，希望对该角度特殊处理：如果该角是目标角，希望其幅度保持不衰减，即$\sum\limits_{k = 0}^{M - 1} {{w^*_k}{e^{ - jk{\theta _0}}}}  = 1$;反之，如果是干扰信号，希望其幅度衰减为0，即$\sum\limits_{k = 0}^{M - 1} {{w^*_k}{e^{ - jk{\theta _0}}}}  = 0$；无论是0还是1，都是对优化问题的一种约束形式，写出更一般的约束形式：

$\sum\limits_{k = 0}^{M - 1} {{w^*_k}{e^{ - jk{\theta _0}}}}  = g$

$g$是一个复增益。利用拉格朗日乘子法给出约束条件下准则函数（暂不考虑噪声情况）：

$J = {{\bf{w}}^H}{R_{xx}}{\bf{w}} + {\mathop{\rm Re}\nolimits} \left[ {{\lambda ^*}\left[ {{{\bf{w}}^H}{\bf{s}}\left( {{\theta _0}} \right) - g} \right]} \right]$

其中${\bf{s}}\left( {{\theta _0}} \right) = \left[ {1,{e^{ - j{\theta _0}}},...,{e^{ - j(M - 1){\theta _0}}}} \right]$,$M$是权向量$\bf{w}$的个数，则到系数解：

$\lambda  =  - \frac{{2g}}{{{{\bf{s}}^H}\left( {{\theta _0}} \right){{\bf{R}}^{ - 1}}{\bf{s}}\left( {{\theta _0}} \right)}}$

对应最优权向量：

${{\bf{w}}_{opt}} = \frac{{{g^*}{{\bf{R}}^{ - 1}}{\bf{s}}\left( {{\theta _0}} \right)}}{{{{\bf{s}}^H}\left( {{\theta _0}} \right){{\bf{R}}^{ - 1}}{\bf{s}}\left( {{\theta _0}} \right)}}$

以权向量${{\bf{w}}_{opt}}$表征的波束形成器称为线性约束最小方差（LCMV, linearly constrained minimum-variance）波束形成器，也称LCMV滤波器。

三、LCMV应用——MVDR算法

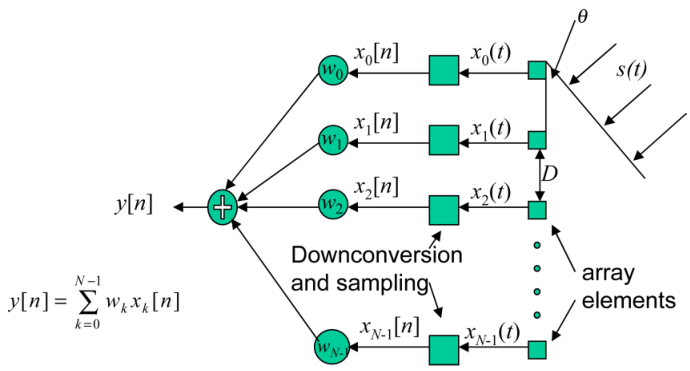
实际应用中信号掺杂了噪声。假设原信号$s(t)$，接收器收集的是不同时延的混合信号，经过采样量化后得$x(n)$，现在希望通过自适应权重$w$输出符合需求的$y$，假设通道个数为$N$，给出接收通道模型：

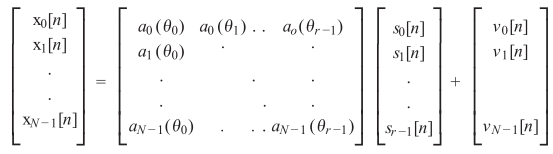
写成矩阵形式：

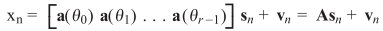
进行相关矩阵求解：

可以发现如果$w^Hw$为定值，则噪声对最优权值的求解无影响，LCMV可用。

给出混合模型：

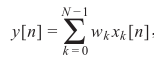
对应准则函数（此处$g = 1$）：

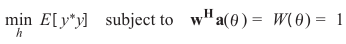
借助LCMV的分析，得出MVDR最优权重：

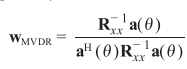
实际应用中，通常用时间换空间，借助遍历性近似求解相关矩阵：

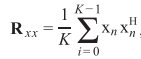
给出代码：

doas=[-30 -5 40]*pi/180; %DOA's of signals in rad.
P=[1 1 1]; %Power of incoming signals
N=10; %Number of array elements
K=1024; %Number of data snapshots
d=0.5; %Distance between elements in wavelengths
noise_var=40; %Variance of noise
r=length(doas); %Total number of signals
% Steering vector matrix. Columns will contain the steering vectors of the r signals
A=exp(-i*2*pi*d*(0:N-1)'*sin([doas(:).']));
% Signal and noise generation
sig=round(rand(r,K))*2-1; % Generate random BPSK symbols for each of the
% r signals
noise=sqrt(noise_var/2)*(randn(N,K)+i*randn(N,K)); %Uncorrelated noise
X=A*diag(sqrt(P))*sig+noise; %Generate data matrix
R=X*X'/K; %Spatial covariance matrix
%MVDR
IR=inv(R); %Inverse of covariance matrix
for k=1:length(angles)
mvdr(k)=1/(a1(:,k)'*IR*a1(:,k));
end
figure;
plot(angles,abs(mvdr)/max(abs(mvdr)),'k');hold on;
xlabel('Angle in degrees')
%Estimate DOA's using the classical beamformer
for k=1:length(angles)
Classical(k)=(a1(:,k)'*R*a1(:,k));
end
plot(angles,abs(Classical)/max(abs(Classical)),'r--');grid on;
legend('MVDR','Classical Beamformer');

对应结果图：

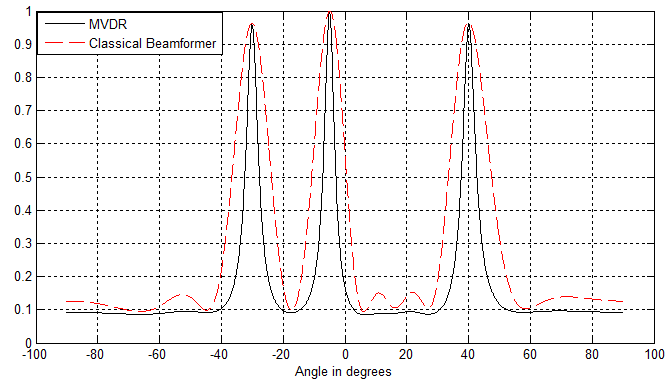
噪声较大时：

二者就比较接近，可以发现：

• 信号与噪声不相关、且噪声为白噪声时，仍能求解最优权值；
• 噪声较大时，MVDR与无约束最优滤波效果接近，此时MVDR的优势不再明显，这也容易理解，噪声占主要成分时对波束的约束保留效果不再明显。

两点补充：

1）因为LCMV中有矩阵求逆一项，所以补充说明一点：默认不同角度信号不相干，只记录学习的理论知识，不论及技术细节处。

2）基于窄带分析。如果是宽带，则可以划分多个自带，或者利用聚焦矩阵预处理，窄带才有如下近似（且一个频带内才可以用一个频率表征）：

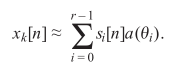
参考：

Jeffrey Foutz, Andreas Spanias, and Mahesh K. Banavar《Narrowband Direction of Arrival Estimation for Antenna Arrays》.

Simon Haykin 《Adaptive Filter Theory Fourth Edition》.