Scipy

插值interpolate模块

计算插值有两个基本方法：

1、对一个完整的数据集去拟合一个函数(一条线穿过所有数据集的点)

2、对数据集的不同部分拟合出不同的函数，而函数之间的曲线平滑对接

一维插值

interp1d(x, y, kind='linear', ...)

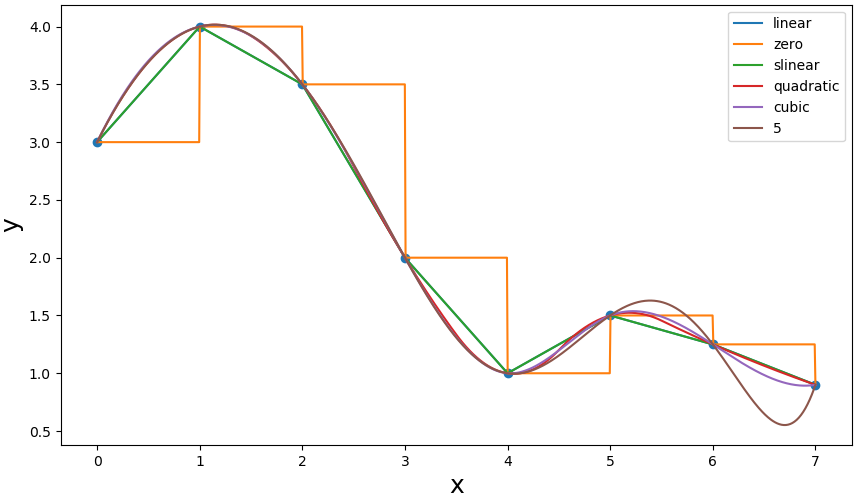
x和y参数是一系列已知的数据点，kind参数是插值类型，可以是字符串或整数，

候选值	作用
"zero"、"nearest"	阶梯插值，相当于0阶B样条曲线
‘slinear’ 、'linear'	线性插值，用一条直线连接所有的取样点，相当于一阶B样条曲线
‘quadratic’ 、'cubic'	二阶和三阶B样条曲线，更高阶的曲线可以直接使用整数值指定

import scipy.interpolate
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import interp1d
# 创建待插值的数据
x= np.array([0, 1, 2, 3, 4, 5, 6, 7])
y= np.array([3, 4, 3.5, 2, 1, 1.5, 1.25, 0.9])
xx = np.linspace(x.min(), x.max(), 1000)    # 设置x的最大值和最小值以防止插值数据越界
fig, ax = plt.subplots(figsize=(8, 4))        # 返回窗口和坐标系
ax.scatter(x, y)                            # 绘制散点图
for n in ['linear','zero', 'slinear', 'quadratic', 'cubic', 5]:
    #      线性、阶梯插值、线性插值、二阶插值、三阶B样条插值
    f = interp1d(x, y, kind = n)            # 得到插值函数
    ax.plot(xx, f(xx), label= n)
ax.legend()
ax.set_ylabel("y", fontsize=18)
ax.set_xlabel("x", fontsize=18)
plt.show()

样条插值

样条插值需要两个基本步骤

1、找到一维曲线的B样条表示

scipy.interpolate.splrep(x, y, xb=None, xe=None, k=3, s=None)

参数：

　　x,y：定义曲线y=f(x)的数据点

　　xb,xe：float 合适的间隔，如果为None,则分别为x[0]和x[-1]

　　k：样条的种类，建议使用3次样条，1 <= k <= 5

　　s：float，平滑度，用户可以使用s来控制贴近度和平滑度之间的权衡。较大的s意味着更平滑，而较小的s意味着较少的平滑。

返回：

　　tck：元组，(t, c, k)包含结矢量，B样条系数和样条程度的元组。

2、在期望点处评估B样条

scipy.interpolate.splev(x, tck, der=0, ext=0)

给定B样条表示的节点和系数，评估平滑多项式及其导数的值。

参数：

　　x：array_like，一组点，样条的节点数

　　tck：元组，由splrep返回的长度为3的系列，包含样条的阶，系数和度数。

　　der：int 要计算的样条的倒数的阶数(必须小于或等于k)

返回：ndarray或ndaray列表，表示在x点处计算 的样条函数的值 的数组。

import numpy as np
import matplotlib.pyplot as plt
from scipy import interpolate
 
x = np.arange(0, 2*np.pi+np.pi/4, 2*np.pi/8)
y = np.sin(x)
tck = interpolate.splrep(x, y)                # 样条插值系数
xnew = np.arange(0, 2*np.pi, np.pi/50)            # 插值范围
ynew = interpolate.splev(xnew, tck)
 
plt.figure()
plt.plot(x, y, 'rx')                            # 散点图
plt.plot(xnew, ynew, "*")                        # 三次样条插值
plt.plot(xnew, np.sin(xnew), "--")                # True
plt.plot(x, y, 'b')                                # 线性插图
 
plt.legend(["Scatter", 'Linear', 'Cubic Spline', 'True'])
plt.axis([-0.05, 6.33, -1.05, 1.05])
plt.title('Cubic-spline interpolation')
plt.show()

参考文献：

数学建模三剑客MSN